Как доказать: Как доказать свою правоту и не остаться в дураках — Право на vc.ru

Оцените эту книгу

Поиск по тексту рецензии

Показано 1–30 из 42 рецензий

Вот как следует думать о математике. Это очень интересная книга, которая объясняет, как работают математические доказательства снизу вверх. В процессе этого он также учит дискретной математике. Кривая обучения была идеальной, чего добиться нелегко. Веллеман объясняет вещи далеко не сухо, но понятно и точно. Я считаю, что каждый, кто сталкивается с математическими доказательствами, должен прочитать эту книгу. Глава, посвященная индукции, особенно полезна, если ваша область практики связана с информатикой.

Мне бы хотелось, чтобы были доступны решения для большего количества упражнений. Поскольку их много, было бы полезно, если бы автор отметил выбранное подмножество как наиболее важное.

информатика

Блин, жаль, что я не прочитал эту книгу ДО поступления в аспирантуру. В этой книге Веллеман делает три вещи:
* описывает основные концепции логики
* дает общие стратегии доказательства с большим количеством примеров
* углубляется в теорию множеств, определение функций и т. д.

Все это он делает, предполагая, что читатель НЕ математик — на самом деле, он отлично справляется с объяснением мыслительного процесса математика, пытающегося что-то доказать.

Я настоятельно рекомендую эту книгу, если вам неудобно читать и/или писать доказательства, так как это сделает чтение следующих книг по математике гораздо более увлекательным!

робототехника

Юмэко

109 отзывов11 подписчиков

На мой взгляд, это было довольно познавательно 🥀.
Меня больше всего беспокоила глава 3 о написании корректуры, но я просмотрел первые две главы и попробовал упражнения, которые не были для меня слишком сложными (удивительно, потому что обычно я не могу решить их в других учебниках по математике, которые я подобрать). Я пробежался по «Математической индукции», к которой, вероятно, вернусь когда-нибудь в будущем с сожалением.
К счастью, книга довольно доступна, и в ней есть ответы на отмеченные звездочкой упражнения (но только для них. Удивительно, почему их никогда нет для всех).

---

6 января 2021 г.

У меня есть первое издание, в котором нет решений, но есть несколько незнакомцев в Интернете, которые решили все проблемы и свободно демонстрируют их в Интернете. Это несколько повторяется, но очень полезно для отработки различных методов доказательства. Я рекомендую последнее издание (3-е на момент написания этого обзора) книги, потому что в конце есть дополнительные упражнения и множество решений, это облегчает проверку, если вы сомневаетесь в себе. Это отличное введение в мышление в виде доказательств и демонстрация вашего умственного процесса аккуратно и правильно.

---

Ахмед

7 отзывов1 последователь

12 января 2008

Эту книгу должен был прочитать каждый, кто занимался исчислением, до того, как он взялся за него. Дрянные учителя в моей школе неправомерно придали математической индукции крутую кривую обучения. Для меня и, я уверен, для многих других эта книга равносильна курсу, отсутствующему в учебной программе по математике.

---

10 октября 2019 г.

Книга, которая научит вас строить хорошо типизированные формулы. Тем не менее, на мой взгляд, это очень далеко от учебника, который может научить вас основам теории множеств, доказательству и/или бесконечным множествам. Вместо этого используйте какую-нибудь другую книгу и читайте эту книгу как дополнительный источник.

---

0vai5

26 отзывов2 подписчика

28 июня 2016 г.

Настоятельно рекомендуется для начинающих, так как это очень помогает в понимании математической строгости.

Автор не ожидает многого от читателя и начинает с самых основных понятий и медленно продвигается к кванторам, затем теории множеств, отношениям и функциям, математической индукции и, наконец, бесконечным множествам.

Во введении автор дает интуитивно понятное доказательство нескольких теорем. Позже, вооружившись всеми методами проверки, все эти доказательства были пересмотрены, и читатель может ясно увидеть разницу в своем понимании чтения и написания доказательств.

Все методы доказательства (кроме индукции) описаны в главе 3. После этого книга представила другие темы, такие как отношения и функции, и использует методы доказательства для доказательства теорем в этих темах. Это был отличный способ продемонстрировать, что методы, изученные для написания доказательств, не зависят ни от какой области и могут применяться в любом месте математики.

Мне нравился метод доказательства от противного и математическая индукция. Взлом соответствующих упражнений был очень полезным опытом. Во многих доказательствах, когда кажется, что ни один подход не работает, на помощь приходит доказательство от противного. Точно так же сила доказательства по индукции проявлялась при решении многих огромных проблем.

Все упражнения были упорядочены от простого к среднему, подготавливая читателя к обучению написанию доказательств для более простых и сложных. Многие упражнения построены на основе теорем предыдущих упражнений. Это хорошо, так как помогло мне в двух отношениях: пересмотреть старые главы и обнаружить ошибки в моих доказательствах.

Было много упражнений, спрашивавших читателя, верно ли данное доказательство. Много раз доказательство выглядело правильным, но оказывалось неверным из-за концептуальной ошибки. Это очень помогло избавиться от многих заблуждений.

В большинстве разделов автор также объясняет, как он пришел к решению, которое помогло понять, как подойти к проблеме.

Наконец, в последней главе автор поднял относительно сложную тему и применяет все изученные методы доказательства. В этой главе автор не вдается в объяснение структуры доказательства, но пишет с математической строгостью, чтобы читатель мог прочитать эти доказательства и получить общее представление о чтении и написании доказательств, уделяя больше внимания теме, чем технике доказательства.

Одна маленькая вещь, которую можно было бы улучшить, это обработка пустых наборов. Я запутался, решая многие упражнения, и чувствовал, что мне не хватает некоторых понятий, касающихся пустых множеств, особенно при работе с семейством множеств.

Подводя итог,
— квантификаторы повсюду.
— Чтение и написание корректуры.
— Теория множеств
— Математическая индукция
— Развил некоторое понимание того, как подойти к проблеме.
— Отлично чувствовал себя в решении многих задач.

В целом, это было отличное начинание и полезный опыт.

Первоначально написано в моем блоге

---

26 августа 2022 г.

Хороший обзор концепций логики, дискретной математики и корректуры. Легко следовать.

---

8 июня 2020 г.

Потрясающая книга, №1 в моем списке «перечитать, если ты умрешь и найдешь себя рожденным свыше». Но как человек, который использовал его для самообучения (если это уместно), я бы немного изменил структуру упражнений.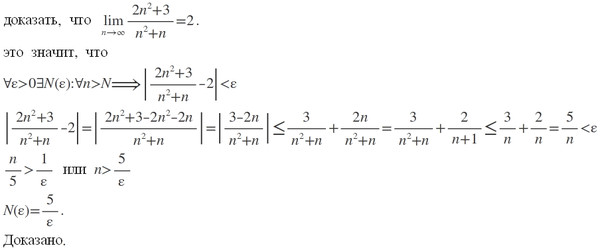 Иногда их бывает слишком много, так что на втором десятке мне становится скучно. В то же время детали затронутых тем часто стирались несколькими абзацами позже. Итак, я бы разделил их таким образом, чтобы самые сложные (номера 20-26) были включены не в конец списка сразу после соответствующего абзаца, а через несколько абзацев в разделе «повторение». Я нашел эту стратегию обучения наиболее эффективной: я уделял все необходимое внимание каждой проблеме и освежал знания о вещах, которые начал забывать.

---

24 сентября 2017 г.

Работа над этой книгой была чрезвычайно полезной. Книга очень логично и доходчиво объясняет, как работают доказательства, и проводит читателя через интересные логические упражнения и полезные темы, такие как теория множеств и счетность. Эта книга является отличной подготовкой к любому серьезному уроку математики, который содержит доказательства (а не просто расчеты и числовые примеры).

Эта книга очень доступна и не требует от ученика необходимых математических знаний.

---

11 июля 2018 г.

Я должен был прочитать что-то подобное много лет назад, в конце средней школы или в начале университета. Я намерен вернуться к нему, так как пропускал все больше и больше упражнений по мере продвижения по тексту. Настоятельно рекомендую людям, которые не любят пруфы!

стебель

---

16 ноября 2022 г.

Я видел, как эту книгу рекомендовали на математических форумах людям, заинтересованным в оттачивании своих навыков корректора. Я определенно подходил под эту категорию, поэтому решил попробовать.

Г-н Веллеман не разочаровывает этим прекрасным изложением искусства составления доказательств. Это ясно, дидактично и очень интересно.

Возможно, это как-то связано с тем, что концепция математического доказательства кажется мне красивой, но на протяжении всей книги я не мог не улыбаться и не испытывать благоговения перед таким возвышенным искусством, как математика.

Однако я не могу поставить этому 5 звездочек из-за того, что я считаю недостаточным объяснением концепций, связанных с наборами. Как только вы дойдете до главы, посвященной отношениям или бесконечным множествам, ясно проявится шаткость фундамента, заложенного случайным образом в первых главах. Это позор, потому что я был взволнован, чтобы копаться в теореме Кантора-Шредера-Бернштейна. Увы, всего в жизни не бывает.

Хорошая книга, достойная внимательного прочтения.

информатика

---

5 октября 2019 г.

Я решил работать над этой книгой в первую очередь для того, чтобы я мог проверить корректуру, и с этой целью книга Веллемана /Как это доказать/ идеально подошла для меня практически по одной причине — есть внушительное количество упражнений.

Написание понятное, и я бы порекомендовал его тем, кто никогда раньше не сталкивался с пруфами. Польза, которую я извлек из этого, заключалась скорее в практике доказательств, а не в обучении тому, как их делать, но всякий раз, когда я забывал что-то основное, я мог просто вернуться и посмотреть, и объяснения не были ужасно увязли в жаргоне.

---

18 января 2021 г.

Как это доказать — еще один «учебник» в списке книг, которые я хотел бы прочитать, будучи студентом колледжа. Теперь, спустя почти десятилетие после выпуска, я возвращаюсь и получаю образование, которое хотел бы получить, когда был моложе, изучая такие книги, как эта и «Базовая эконометрика Гуджарати ».

Название книги полностью описывает ее назначение: How to Prove It содержит углубленный курс о том, как писать доказательства. Всем, кто планирует пройти курсы математики на уровне колледжа (помимо исчисления) и хочет действительно преуспеть в них, следует прочитать эту книгу.

---

THN

107 отзывов4 подписчика

30 ноября 2019 г.

Автор очень терпеливо объясняет подробности читателям, но иногда это становится слишком длинным и запутанным. Содержание правильное и строгое, но есть небольшие неточности (опечатки или нюансы в обозначениях, во втором издании). В целом, это хорошая книга, чтобы начать знакомиться с математическими доказательствами, не слишком опасаясь самостоятельно прочитать полное доказательство. Было бы лучше, если бы некоторые части стали более краткими.

Математика для науки

---

24 июля 2020 г.

Солидное введение

Солидное введение и обзор логических доказательств в математике. Охватывает логику высказываний и логику предикатов первого порядка, математическую индукцию и основные понятия теории множеств. Много подробных примеров. На самом деле слишком много. Время ограничено!
Необходимо улучшить форматирование электронной книги. Это только усложняет чтение. Отлично подходит для начинающих. Полезный обзор/напоминание для других.

---

25 октября 2020 г.

Эта книга оказала (и продолжает оказывать!) огромную помощь в подготовке к изучению математики в университете. Многие лекторы в основном пропускают приемы доказательства, подробно описанные автором в этой книге. Благодаря отличным упражнениям в конце каждой главы у меня гораздо меньше проблем с действительно сложными и абстрактными упражнениями в нашем обычном учебнике, потому что я научился искать конкретные структуры, которые объясняет автор.

---

13 июля 2020 г.

Это был мой учебник по курсу дискретной математики.
Это ценная книга главным образом потому, что она на самом деле учит вас, как писать хорошо построенные доказательства.
Каждая глава раскрывает свои гениальные доказательства с примененными за кулисами стратегиями и множеством примеров, демонстрирующих процесс написания корректуры.
Также в книгу включены сложные упражнения. Настоятельно рекомендуется!

---

4 сентября 2019 г.

Замечательная книга, которая знакомит с практическими стратегиями доказательства различных вещей в математике и делает все виды доказательств доступными для начинающих студентов, немалое достижение!

---

Лукаш

171 отзыв12 подписчиков

Хочу прочитать

13 мая 2020 г.

рекомендация: [Спросите HN: Как я могу научиться читать математические обозначения? | Hacker News](https://news.ycombinator.com/item?id=…)

вводная математика

---

20 августа 2020 г.

Одинаково подходит для продвинутого старшеклассника или учащегося первых двух лет обучения свое обучение в бакалавриате.

Отличное средство от беспокойства.

на полке

---

13 декабря 2021 г.

Хороший материал для чтения, но может показаться слишком здравым. Возможно, это поможет вашей интуиции, но дискретный учебник по математике с большим количеством практических задач, вероятно, поможет больше.

обучение вере

---

14 декабря 2022 г.

Увлекательное чтение множества задач отлично подходит для тех, кто не имеет большого опыта в логике или математике. Больше нечего сказать, настоятельно рекомендую как новичкам, так и профессионалам!

---

21 декабря 2020 г.

Эта книга утомительна, но, в конечном счете, полезна для прилежного новичка, который хочет или может много практиковаться.

Я никогда не был так хорош в корректуре в университете. Я купил эту книгу, чтобы помочь. Тогда это было не так, но стало для меня более ценным, когда я готовлюсь ко второму раунду моей борьбы с математикой.

В этой книге есть три ценные идеи:
(1) Вся математика построена на иерархии логики и определений, поэтому более крупные термины можно разбить на более мелкие (функции определяются как предикаты, определяются как множества определяются как высказывания, определяются как термины со связками, которые вместе являются истинными или ложными).
(2) Построение доказательств, а не таинственность, представляет собой систематический процесс, который можно осуществить, применяя правильное правило к вашим утверждениям снова и снова.
(3) Поскольку эта иерархия полностью ясна, а правила совершенно ясны, если вы разобьете утверждение на его простейшие части и постепенно примените к ним правильные правила, вы сможете доказать это.

То, что вы должны ожидать от этой книги, — это путь к внедрению этих уроков. Но если у вас есть время, есть книги, которые я бы порекомендовал до этого, и книги, которые я бы порекомендовал после.

Альтернативная книга — «Введение в математическое мышление» Кита Девлина. Это более педагогично, чем «Как это доказать», поскольку требуется время, чтобы объяснить роль точного языка в математике, таким образом объясняя, почему определенные правила являются такими, какие они есть (включая то, почему вы отрицаете вторую часть предложения, а не первую часть). , или почему что-то ложное может подразумевать, что что-то другое истинно, но не наоборот). В качестве бонуса к Веллеману к книге прилагается курс Coursera.

Книгой, которая сделала математику доказательства действительно интересной для меня, была «Логический подход к дискретной математике» Грайса и Шнайдера. Они учат другому, но родственному методу доказательства, называемому эквациональной логикой. Это стоит упомянуть, потому что они обнаружили, что некоторые ученики учатся лучше с этим стилем, поскольку это почти то же самое, что упрощение арифметических функций, как мы делали в начальной школе, и это даже более механистично, чем подход Веллемана «данные и цели». Веллеман также неявно использует этот подход, когда упрощает свои выражения перед их вычислением. Тем не менее, ALAtDM в некотором смысле является более сложной книгой, так как в ней нет решений, а изложение очень краткое. Вы по-прежнему можете найти решения в Интернете, если они вам нужны, и если вам нужно больше отзывов, чтобы начать работу, я бы порекомендовал эту книгу как вторую.

Почетное упоминание получает книга Дэниела Солоу «Как читать и делать корректуры», которую можно рассматривать как краткое изложение книги Веллемана, даже если она написана другим автором. Солоу строит свою книгу вокруг так называемого «метода прямого-обратного», который аналогичен подходу Веллемана к использованию данных и целей для поиска способов завершения доказательства посередине. Это делает «Как это доказать» надмножеством Солоу, но если у вас меньше свободного времени, Солоу может быть достаточно хорош. Примечание: в отличие от Веллемана, «Как читать и делать доказательства» не охватывает теорию множеств и логику предикатов, поэтому, если это важно для вас, выберите Веллемана.

---

Дэус

300 отзывов3 подписчика

12 марта 2019 г.

Мне нравится, как структурирована эта книга, особенно первая половина (именно там у меня было большинство моментов «ах-ха!»). Каждый раздел мастерски построен на предыдущем. Это заполнило для меня много пробелов в моей математике и понимании логики, даже после того, как я изучал математику в бакалавриате. Мне потребовалось больше года, чтобы пройти через это, и, хотя временами это было довольно жестоко, я очень благодарен за эти знания. Я бросил попытки выполнять упражнения через несколько глав после раздела доказательств, так как это было больше связано с чтением доказательств, а не с освоением методов.

Я думаю, что работа в области программирования/аналитики после колледжа действительно помогла мне понять логический синтаксис и концепции доказательств, с которыми я так мучился в колледже. Моими главными пробелами были на самом деле сентенциальная логика, понимание прочитанного/терпение и непонимание некоторых основных определений (т. е. существование, уникальность, на, противопоставление и т. д.).

Цитаты:
— «Чтобы убедиться, что ваши утверждения адекватно обоснованы, вы должны скептически относиться к каждому выводу в вашем доказательстве. это не так. В конце концов, если ваши собственные рассуждения даже не убеждают вы , как вы можете ожидать, что это убедит кого-то еще?»
— «Когда математики пишут доказательства, они обычно просто пишут шаги, необходимые для обоснования своих выводов, без объяснения того, как они их придумали… Хотя этого недостает объяснения иногда затрудняет чтение доказательств, оно служит цели разделения двух различных целей: объяснение вашего мыслительного процесса и обоснование ваших выводов . Первый — это психология, второй — математика… Иногда в очень сложном доказательстве математик может включить некоторое обсуждение стратегии, стоящей за доказательством, чтобы его было легче читать. Обычно, однако, читатели сами в этом разбираются». Это так много объясняет…
— «Важно придерживаться изученных нами правил проверки корректуры, а не позволять себе быть убежденным любыми рассуждениями, которые выглядят правдоподобными… Только превратив свою идею в формальное доказательство, вы можете быть уверен, что ваш ответ правильный. Часто в ходе попыток построить формальное доказательство вы обнаружите недостаток в своих рассуждениях… и вам, возможно, придется преодолеть этот недостаток. Окончательная теорема и доказательство часто являются результатом повторяющихся ошибок и поправки … только потому, что математики не объясняют свои ошибки в своих доказательствах, вы не должны обманываться, думая, что они их не делают!»

math-econ-psych

---

18 февраля 2014 г.

«Как это доказать» — замечательный учебник по различным методам, которые можно использовать для доказательства математических теорем с использованием логики для первокурсников. Она очень хорошо написана с точки зрения человека с небольшими математическими познаниями, выходящим за рамки школьной математики. Как человек, который любит систематическое мышление, точность и строгость, я действительно наслаждался путешествием от простых, обычных доказательств к доказательствам, включающим различные размеры бесконечности. И хотя я не совсем все понял, это потому, что я прочитал книгу от корки до корки, не отрываясь; но я намерен вернуться к началу и действительно проработать многие (многие!) упражнения в тексте. Книге суждено стать классикой. Я очень рекомендую это!

---

5 июля 2012 г.

Книга дает то, что обещает — структурированный подход к доказательствам. Это может быть немного сложно, но развивает теорию с нуля и проводит читателя с самого начала. Ближе к концу Веллеман довольно быстро продвигается по материалу, предполагая, что читатель усвоил весь предыдущий материал, что хорошо, но создает некоторые трудности. Переход от множеств к отношениям, функциям и мощности протекал хорошо. В конце книги также есть много полезных интересных упражнений и много предложений и полных решений.

---

15 января 2017 г.

В этой книге представлены доказательства и показан лежащий в их основе логический механизм. Особое внимание уделяется языку математической логики.