Квадрат декарта пример для работы: Квадрат Декарта для принятия решений в личной жизни

Квадрат Декарта для принятия решений, пример

/ Информационная сфера / От texvi / 2022-07-16

Квадрат Декарта для принятия решений это таблица с четырьмя вопросами. И прежде чем принять решение вам необходимо ответить на них. Метод простой, как все гениальное.
Люди в основном не правильно подходят к решению проблемы, поэтому во многих случаях принимают не верные решения. Квадрат Декарта для принятия решений поможет найти самое оптимальное решение проблемы. Научитесь им пользоваться на примере.
Пример:
Необходимо как можно точнее отвечать на заданные вопросы в этой таблице, будьте честны с собой и уберите все иллюзии, необходимо четко и без эмоций ответить на эти четыре вопроса.
В этом примере мы рассмотрим проблему смены рода деятельности, но вместо нее можно поставить любую проблему которая вас беспокоит (смена жительства, операция по коррекции, в какой дет. сад отдавать ребенка, куда поступать учиться).
Узнайте с квадратом Декарта все перспективы и пути решения проблемы.

Справочные таблицы которые помогают в различных сферах вашей жизни.

1 вопрос из таблицы «Квадрат Декарте»:

Что будет, если это произойдёт? (Набирайтесь терпения и прочитайте все до конца, иначе вы просто не поймете принцип действия квадрата Декарта).
Данный вопрос подразумевает поиск плюсов от получения желаемого. Под словом «это» следует иметь в виду реализацию принимаемого решения. Первый вопрос является наиболее очевидным и по этой причине очень важно находить как можно больше ответов, т.е. не останавливаться на том, что первым приходит на ум. Ответы на этот вопрос будут служить вам мотивацией к принятию решения.

Что будет, если я поменяю род деятельности?

Если я поменяю род деятельности, я сделаю первый шаг к своей мечте – заниматься тем, чем мне действительно нравится.
Если я поменяю род деятельности, я смогу перестать работать «на дядю» и сам контролировать и свою работу, и свой доход.
Если я поменяю род деятельности, это скажет о моей смелости, и я стану больше уважать самого себя.
Если я поменяю род деятельности, я смогу доказать тем, кто меня окружает, что серьёзно намерен изменить свою жизнь.
Если я поменяю род деятельности, это станет моей мотивацией к получению новых знаний, овладению новыми навыками.
Если я поменяю род деятельности, смогу скорее начать заниматься чем-то новым.
Если я поменяю род деятельности, я перестану сомневаться насчёт правильности своего выбора.

2 вопрос из таблицы «Квадрат Декарте»:

Что будет, если это НЕ произойдёт?
Данный вопрос подразумевает поиск плюсов от неполучения желаемого. Другими словами, ответы на второй вопрос покажут вам, что случится, если вы откажетесь от реализации принимаемого решения, и всё останется так же, как и было раньше. Отвечая, записывайте все преимущества настоящего положения дел, которые вы не хотели бы потерять.

Что будет, если я не поменяю род деятельности?

Если я не поменяю род деятельности, мне не нужно будет отказываться от привычного образа жизни.
Если я не поменяю род деятельности, я не буду переживать по поводу того, что придётся осваивать новые знания и учиться новым вещам, ведь это может не получиться.
Если я не поменяю род деятельности, я смогу спокойно отдыхать в свои выходные дни.
Если я не поменяю род деятельности, мне не нужно будет ни перед кем объясняться или оправдываться.
Если я не поменяю род деятельности, я смогу подумать об этом в будущем. Возможно, действительно стоит повременить.
Если я не поменяю род деятельности, я смогу предаваться грёзам о том, как занимаюсь тем, что мне действительно нравится.
Если я не поменяю род деятельности, я докажу окружающим меня людям, что меня устраивает текущее положение дел.

Вы руководитель или человек который отвечает за привлечения клиентов в ваш уже процветающий бизнес (или вы стремитесь к этому)? Это для Вас.

3 вопрос из таблицы «Квадрат Декартене«:

Чего НЕ будет , если это произойдёт?
Данный вопрос подразумевает поиск минусов от получения желаемого.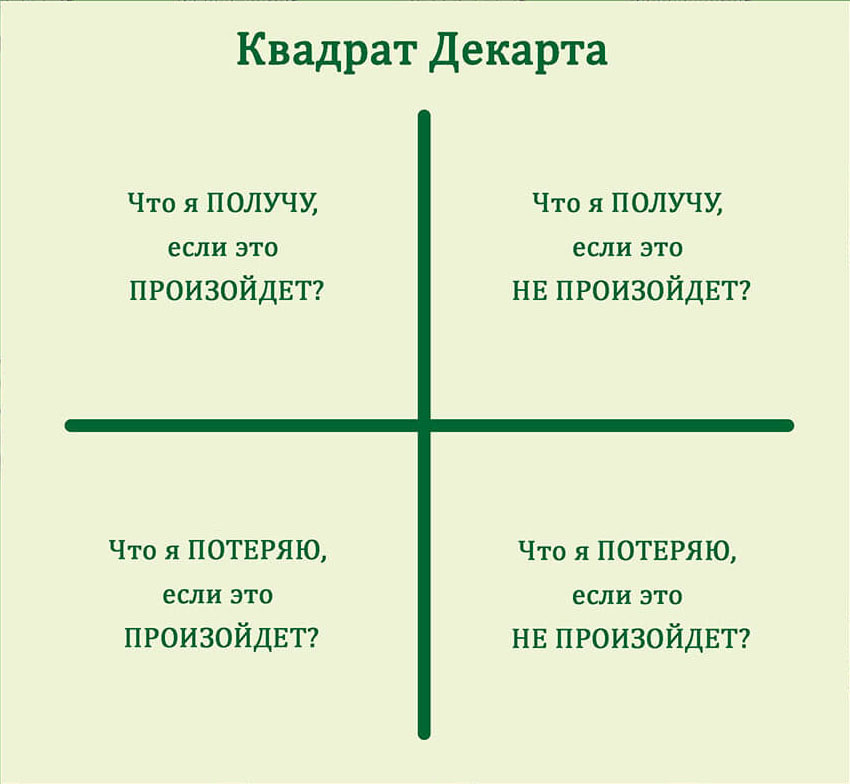 Проще говоря, ответы на третий вопрос будут представлять собой ту цену, которую вы должны будете заплатить за реализацию принимаемого решения.

Чего не случится, если я поменяю род деятельности?

Если я поменяю род деятельности, я уже не смогу жить той жизнью, к которой так привык за много лет.
Если я поменяю род деятельности, я уже не смогу откладывать действия по поиску новых возможностей.
Если я поменяю род деятельности, я уже не смогу отдыхать в привычные для меня выходные дни.
Если я поменяю род деятельности, у меня уже не будет достаточного количества времени на бесцельное, но приятное времяпрепровождение.
Если я поменяю род деятельности, у меня уже не будет возможности общаться с прежними коллегами и ходить на весёлые корпоративы.
Если я поменяю род деятельности, ко мне уже не будет прежнего отношения окружающих меня людей.

4 вопрос из таблицы «Квадрат Декартене«:

Чего НЕ будет, если это НЕ произойдёт?
Данный вопрос подразумевает поиск минусов от неполучения желаемого. Отвечая на четвёртый вопрос, вы отсекаете оставшиеся «не», мешающие реализации принимаемого решения. На этом этапе рекомендуется отвечать, как можно быстрее, опираясь на интуицию.

Чего не случится, если я не поменяю род деятельности?

Если я не поменяю род деятельности, у меня не появится возможности реализовать свою мечту – зарабатывать, занимаясь тем, что мне действительно нравится.
Если я не поменяю род деятельности, я не смогу перестать работать «на дядю», а значит, не смогу самостоятельно контролировать свою работу и свой доход.
Если я не поменяю род деятельности, я не стану больше уважать себя, т.к. покажу страх перед переменами в жизни.
Если я не поменяю род деятельности, никто (в том числе, и я сам) не поверит в серьёзность моих намерений изменить жизнь.
Если я не поменяю род деятельности, у меня так и не появится мотивации к получению новых знаний и овладению новыми навыками.
Если я не поменяю род деятельности, я не смогу избавиться от своих сомнений и так и останусь в переживаниях по поводу того, что не принял решения.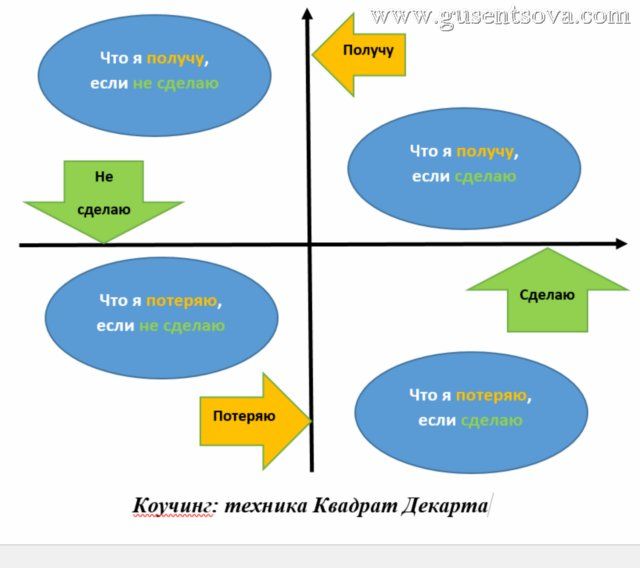

5 вопросов про Квадрат Декарта для принятия решений

Квадрат Декарта – способ принятия решений в личной жизни и работе, который позволяет глубоко проанализировать ситуацию и учесть все плюсы и минусы. Если у вас сложный выбор из разряда «ДА или НЕТ», «ДЕЛАТЬ или НЕ ДЕЛАТЬ», эта техника подойдет идеально.

На консультациях я люблю использовать Квадрат Декарта для принятия решений в личной жизни клиента. Потому что после того, как мы всё расчертим и запишем, решение становится очевидным. Мои клиентки иногда удивляются, как можно было столько времени тянуть кота за хвост и раздумывать.

Содержание

• Вопрос 1. Как пользоваться Квадратом Декарта для принятия решений?
• Вопрос 2. Как избежать типичных ошибок?
• Вопрос 3. Как применять Квадрат Декарта в работе? (пример)
• Вопрос 4. Как использовать Квадрат Декарта в личной жизни? (пример)
• Вопрос 5. Почему не получается принять решение по технике Квадрат Декарта?

Вопрос 1.

Как пользоваться Квадратом Декарта для принятия решений?

Расчертите лист бумаги на 4 части.

Подпишите заголовки в верхней части каждой ячейки, чтобы было проще ориентироваться:

• ПЛЮСЫ, если ДА
• МИНУСЫ, если ДА
• ПЛЮСЫ, если НЕТ
• МИНУСЫ, если НЕТ

Примерно так, как на рисунке:

Есть другой вариант заполнения.

В этом варианте вы думаете не про ПЛЮСЫ/МИНУСЫ, а именно про НАЛИЧИЕ/ОТСУТСТВИЕ каких-то факторов в каждом случае. На мой взгляд, это прямой путь к тому, чтобы окончательно запутаться, но люди разные. Возможно, такой способ вам понравится больше.

И тогда ячейки будут такие:

• Что будет, если это произойдет?
• Чего не будет, если это произойдет?
• Что будет, если это не произойдет?
• Чего не будет, если это не произойдет?

Вот рисунок, чтобы было понятнее:

Теперь ваша задача – записать всё, что приходит в голову по вашей ситуации. Записывать – обязательно. Пока вы просто крутите мысли в голове, они там живут одним спутанным комком. Когда вы выложите это на бумагу, вы сможете рассортировать все ваши мысли, надежды, сомнения по ячейкам. Так появляется не только ясность, но и возможность увидеть новые пути решения.

Итак, запишите в ячейки:

ПЛЮСЫ, если ДА

Улыбнитесь и постарайтесь размышлять легко, позитивно, оптимистично. Что вы получите, если решитесь? Какие выгоды – финансовые, психологические, социальные?

МИНУСЫ, если ДА

Вот здесь пришло время внутреннему критику, можно дать ему волю. Какие минусы? Какие проблемы возникнут сейчас или в долгосрочной перспективе, если принять такое решение?

ПЛЮСЫ, если НЕТ

Аналогично рассмотрите в подробностях вариант, когда решение НЕ принято. Какие плюсы будут, если это не произойдет? Что хорошего в том, чтобы оставить всё как есть?

МИНУСЫ, если НЕТ

Ну, и напоследок опишите всё то, что мешает вам вообще ничего не делать.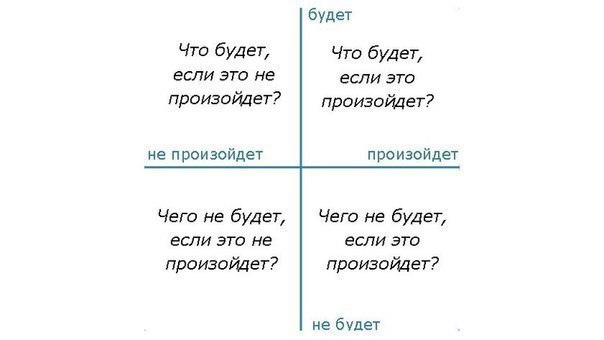 Какие проблемы будут, если вы не примете это решение?

Вопрос 2. Как избежать типичных ошибок?

Во-первых, подбирайте короткие формулировки.
Когда мысль сформулирована длинно, нашему мозгу сложно с ней работать. Поэтому, если не укоротить заранее, то скорее всего, вы потом для простоты мысленно обрежете как получится. И не факт, что получится хорошо, можно так упустить важный нюанс.

Во-вторых, будьте честны с собой.
Если вы не уверены, плюс это или минус, пишите сразу в обе ячейки.
Пример: «Придется сесть на диету» — это минус, потому что не хочется себя ограничивать, но плюс, потому что как раз хотела скинуть несколько килограммов.

В-третьих, заполняйте ячейки в любом порядке.
Не старайтесь сначала выписать только плюсы, а потом – только минусы. Или сначала только про один вариант решения, а потом – про другой. Пишите в том порядке, в котором приходит в голову, иначе эти мысли всё равно будут маячить в голове и отвлекать.

В-четвертых, оставьте принятие решения на потом.
Дело в том, что выгрузка информации и её анализ – это два совершенно разных процесса для нашего мозга. И если вы переключаетесь на анализ, вы автоматически блокируете выгрузку. Сначала запишите всё, что приходит в голову, даже самые очевидные мысли. Не пытайтесь делать какие-то выводы и принимать решение до тех пор, пока этот поток не иссякнет.

Вопрос 3. Как применять Квадрат Декарта в работе? (пример)

Елена размышляет, стоит ли ей остаться работать в офисе, где она занимает неплохую должность вот уже 7 лет. Или всё-таки сменить род деятельности и уйти на фриланс.

ПЛЮСЫ, если ДА (Если уйти на фриланс)

• Возможность переехать в другой город
• Повышение дохода в перспективе
• Интересная работа
• Обучение и развитие
• Возможность перевести сына на семейное обучение

МИНУСЫ, если ДА (Если уйти на фриланс)

• Не будет отпуска в этом году
• Нужно искать заказы самой
• Родители не поймут, почему ухожу с хорошей стабильной работы
• Дома нет рабочего места
• Придется самой себя организовывать

ПЛЮСЫ, если НЕТ (Если не менять работу и остаться на прежней должности)

• Стабильная зарплата
• Работа по основной специальности
• Хороший коллектив, общение
• Можно обратиться за советом к коллегам

МИНУСЫ, если НЕТ (Если не менять работу и остаться на прежней должности)

• Ощущение, что упустила свой шанс
• Долгая дорога на работу
• Раздражение на начальницу

Для более подробного анализа вашей жизненной ситуации вам больше подойдет техника «Колесо Баланса». Подробное описание техники и готовые шаблоны для скачивания вы найдете в этой статье: «Колесо Баланса Жизни 12 сфер — шаблон и инструкция» (откроется в новом окне)

 

Вопрос 4. Как использовать Квадрат Декарта в личной жизни? (пример)

Ольга думает, отдавать ли дочь в сад или подождать еще годик. Решение вопроса затрудняет еще и то, что нужно учесть интересы всей семьи.

ПЛЮСЫ, если ДА (дочь идет в сад)

• Плавная подготовка к школе для дочки
• Общение со сверстниками, дочка очень общительная
• Возможность мне выйти на работу хотя бы на полставки
• Смогу ходить в спортзал и привести себя в порядок

МИНУСЫ, если ДА (дочь идет в сад)

• Дочке будет сложно адаптироваться, она очень ко мне привязана
• Влияние чужих людей (воспитателей) на ребенка
• Постоянные сопли и ОРВИ
• Отводить в сад придется мужу, не уверена, что он готов взять это на себя.

ПЛЮСЫ, если НЕТ (Сижу с дочкой дома еще год)

• Свобода передвижения, возможность уехать хоть на месяц
• Возможность проводить много времени с дочкой
• Есть отговорка, почему не выхожу на работу

МИНУСЫ, если НЕТ (Сижу с дочкой дома еще год)

• Придется продолжать просить помощи у мамы
• Теряю квалификацию в своей специальности
• Напрягает статус «домохозяйки», отдаляюсь от подруг
• Полностью финансово завишу от мужа

Вопрос 5.

Почему не получается принять решение по технике Квадрат Декарта?

Часто уже в процессе выполнения техники становится очевидно, как поступить для вас будет хорошо и правильно. Но может возникнуть несколько сложностей.

1 сложность: ваша интуиция подсказывает одно, а разум – другое.

Для того, чтобы избежать внутреннего сопротивления, необходимо не только обдумать ситуацию, но и прислушаться к интуиции. По сути, интуиция – это тот жизненный опыт, который накопился у вас к текущему моменту. Глупо этот опыт не использовать.

Разница между интуицией и осознанным разумным решением – как разные режимы освещения в комнате.

• Рациональные размышления и анализ ситуации – это яркий узкий луч света, который падает от настольной лампы. Вы хорошо видите то, что поместите под лампу, но комната останется во тьме.
• Интуиция – как рассеянное освещение в комнате в предрассветный час или на закате. Нюансы и подробности не видны, но вы легко можете оценить картину целиком, составить общее впечатление.

Какой подход лучше – рациональный или интуитивный? К чему стоит прислушиваться в первую очередь – к разуму или интуиции? Ведь для принятия серьезных решений лучше бы видеть не только проблему «под лампой», но и обстоятельства жизни целиком.

Всё зависит от того, как много у вас опыта в той сфере, где нужно принять решение. Чем больше опыта и знаний уже есть, тем больше можно полагаться на интуицию. Если с подобными вопросами вы почти не сталкивались, предпочтительнее рациональный подход.

2 сложность: вы знаете, как поступить правильно, но это слишком страшно.

Техника Квадрат Декарта хороша, чтобы принять решение, опираясь на разум. Но что делать, если головой всё понимаешь, но очень страшно решиться.

Бояться – нормально. Это защитный механизм, он удерживает нас от опасных и необдуманных решений. Смелые люди – не те, кто не боится. Это те, кто делает то, что нужно, не смотря на страх.

Не спрашивайте себя, почему вы боитесь. Не пытайтесь бороться со своим страхом. Задайте себе другой вопрос: правильно ли мне в этой ситуации бояться? И если да, то чего именно бояться – правильно?

Представьте, что случилось то страшное, чего вы ожидаете. Сможете ли вы справиться с этой ситуацией? Хватит ли у вас умений, знаний, навыков, денег и других ресурсов, чтобы решить возникшие проблемы? Сможете ли вы жить счастливо после этого?

Пока вы оцениваете вероятность возникновения проблем, вы будете бояться и тревожиться всё больше. Вместо этого оценивайте свою готовность с этими проблемами справиться.

Не пытайтесь сделать так, чтобы нежелательное не случилось. Думайте о том, где подстелить соломки и как укрепить свои позиции, чтобы справиться с проблемой, если она будет.

3 сложность: оба варианта решения примерно равнозначны

Так бывает, если на самом деле варианты равнозначны по совокупности всех факторов. И тогда не важно, что вы выберете. Главное – выбрать, и поскорее.

Пока вы бесконечно анализируете плюсы и минусы моделей смартфонов, чтобы выбрать идеально вам подходящий, вы не замечаете одной важной детали. Всё это время вы ходите со старым смартфоном. Вы терпите его разбитый экран, неработающие приложения, бесконечно медленную загрузку.

Ничего не выбирать – это тоже выбор.

Кроме того, бывает, что есть скрытые вторичные выгоды от того, что ситуация не решается. Задумайтесь, что вы можете делать или не делать, пока решение не принято. Если вы не найдете, как эти свои потребности удовлетворить по-другому, вы будете неосознанно затягивать решение вопроса.

Почитайте также статью «Как победить лень и заставить себя что-то делать». Там подробнее о том, почему возникает внутреннее сопротивление и как себя мотивировать.

Самое главное, не нужно идти сложным путем там, где можно по-простому.

Некоторые решения мы принимаем вообще не задумываясь. И это хорошо, потому что экономит силы и время. Представьте, что было бы, если бы каждое утро вы размышляли, нужно ли чистить зубы.

Если цена ошибки действительно велика, и выбрать сложно, используйте технику Квадрат Декарта для принятия решений в личной жизни и в рабочих ситуациях.

И если уж совсем вопрос никак не решается, а время поджимает, идите к психологу. Иногда, чтобы найти достаточно хорошее решение, нужно просто загрузить свою проблему в чью-то еще голову.

Подпишитесь на мой Telegram-канал, чтобы получать новые статьи и психологические разборы реальных ситуаций.

Вам также могут быть интересны статьи:

• Колесо Баланса Жизни 12 сфер — шаблон и инструкция
• Как победить лень и заставить себя что-то делать
• ТОП 23 книги для саморазвития и самосовершенствования (личный опыт)

math — Размещение квадратов на декартовой плоскости и вычисление их координат X, Y на основе порядкового номера

(При редактировании: я добавил вторую функцию, которая позволяет напрямую получать декартову версию координат.)

Я зашел так далеко прежде чем моя голова взорвалась. Это закрытая форма в том смысле, что она дает координаты, скажем, миллионного квадрата без необходимости размещать их одну за другой в цикле.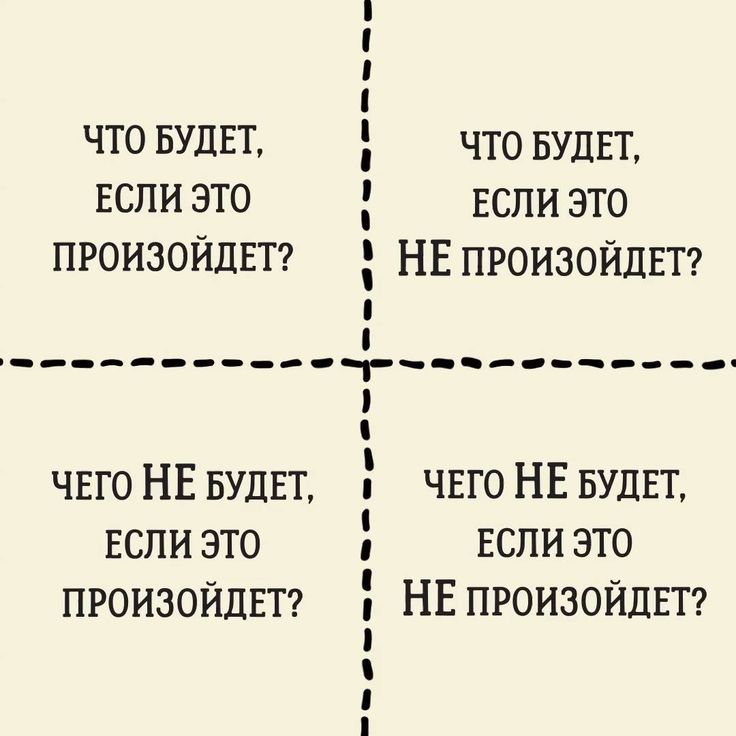 Записав это, вы не получите хорошей формулы, но вы можете написать кусочно определенную формулу с 8 частями. Ответ дается в координатах сетки на основе 1. Первая координата сообщает вам, на сколько квадратов вы находитесь справа или слева от оси Y, а вторая координата — как далеко вверх или вниз. Из этих чисел относительно легко, например. получить декартовы координаты их верхнего левого угла. Я реализовал это на Python:

 из импорта математики sqrt, ceil
Координаты защиты (м):
    n = ceil(sqrt(m)/2) #номер оболочки
    i = m - 4*(n-1)**2 #индекс в оболочке
    если я <= п:
        вернуть (n,-i)
    Элиф я <= 2*n-1:
        возврат (2*n - я, -n)
    Элиф я <= 3*n - 1:
        возврат (2*n - 1 - я, -n)
    Элиф я <= 4*n - 2:
        возврат (-n, -4*n + 1 + i)
    Элиф я <= 5*n - 2:
        возврат (-n, -4*n + 2 + i)
    Элиф я <= 6*n - 3:
        возврат (-6*n + 2 + i, n)
    Элиф я <= 7*n - 3:
        возврат (-6*n + 3 + i,n)
    еще:
        возврат (n, 8*n -3 - i)
 

Чтобы получить декартовы координаты (x,y) верхних левых углов из координат сетки (i,j), вы можете использовать следующую функцию, которая имеет необязательный параметр ширины, позволяющий использовать неединичные квадраты:

 def cartesianFromGrid(i,j,w = 1):
    x = w * (i, если i <0, иначе i - 1)
    y = w * (j, если j >
  0, иначе j + 1)
    возврат (х, у)
 

Можно напрямую получить декартовы координаты верхнего левого угла без предварительного прохождения координат сетки. Полученная формула включает меньше случаев (поскольку мне не нужно сразу переходить от 1 к -1 или наоборот), хотя я сохраняю обе формулы в ответе, поскольку во многих отношениях перспектива сетки более естественна:

 def cartКоординаты(м):
    n = ceil(sqrt(m)/2) #номер оболочки
    i = m - 4*(n-1)**2 #индекс в оболочке
    если я <= п:
        возврат (n-1,-i+1)
    Элиф я <= 3*n - 1:
        возврат (2*n - 1 - я, -n + 1)
    Элиф я <= (5*n - 2):
        возврат (-n, -4*n + 2 + i)
    Элиф я <= 7*n - 3:
        возврат (-6*n + 2 + i, n)
    еще:
        возврат (n-1, 8*n-3-i)
 

Вывод для 1-16:

 >>> для n в диапазоне (1,17):
    print(n, ': координаты сетки =', координаты(n),
          'Декартово =',cartesianFromGrid(*координаты(n)))
1 : координаты сетки = (1, -1) Декартово = (0, 0)
2 : координаты сетки = (-1, -1) Декартова = (-1, 0)
3 : координаты сетки = (-1, 1) Декартово = (-1, 1)
4 : координаты сетки = (1, 1) Декартова = (0, 1)
5 : координаты сетки = (2, -1) Декартова = (1, 0)
6 : координаты сетки = (2, -2) Декартова координата = (1, -1)
7 : координаты сетки = (1, -2) Декартова координата = (0, -1)
8 : координаты сетки = (-1, -2) декартовы координаты = (-1, -1)
9: координаты сетки = (-2, -2) Декартовы координаты = (-2, -1)
10 : координаты сетки = (-2, -1) Декартова координата = (-2, 0)
11 : координаты сетки = (-2, 1) Декартово = (-2, 1)
12 : координаты сетки = (-2, 2) Декартово = (-2, 2)
13 : координаты сетки = (-1, 2) Декартова = (-1, 2)
14 : координаты сетки = (1, 2) Декартова = (0, 2)
15 : координаты сетки = (2, 2) Декартова = (1, 2)
16 : координаты сетки = (2, 1) Декартова = (1, 1)
 

Если вам интересно:

 >>> координаты (1000000)
(500, 1)
 

Этот последний ответ имеет смысл, поскольку миллионный квадрат является краеугольным камнем сетки квадратов 1000x1000.

Я использовал приведенное выше для размещения цветных квадратов на виджете tkinter canvas:

Декартово произведение и упорядоченные пары

В теории множеств декартово произведение двух множеств является произведением двух непустых множеств заказанный способ. Декартово произведение   состоит из двух слов – декартово и произведение. Слово «картезианец» названо в честь французского математика и философа Рене Декарта (1596–1650). В этой статье вы узнаете определение декартова произведения и упорядоченной пары со свойствами и примерами.

Декартово произведение множеств

Декартово произведение множеств дает множество, включающее в себя наборы всех упорядоченных пар.

Предположим, что A и B — два набора, такие что A — набор из 3 цветов, а B — набор из 2 объектов, т. е.

A = {зеленый, черный, красный}

Б = {б, р},

, где b и p обозначают селективный мешок и ручку соответственно.

Давайте найдем, сколько пар цветных предметов мы можем составить из этих двух наборов, A и B.

Пройдя довольно тщательно, мы можем определить, что будет шесть разных пар. Их можно записать, как указано ниже:

(зеленый, b), (зеленый, p), (черный, b), (черный, p), (красный, b), (красный, p)

Пары, упорядоченные выше, представляют собой декартово произведение заданных двух множеств.

Что такое декартово произведение и упорядоченные пары?

Декартово произведение двух непустых множеств A и B обозначается как

\(\begin{array}{l} A × B \end{array} \)

и определяется как «набор всех упорядоченных пар ( a,b ) таких, что

\(\begin{array}{l} a \in A \end{array} \)

и

\(\begin {array}{l} b \in B \end{array} \)

 “.

\(\begin{array}{l}~~~~~~~~~~~~~~\end{array} \)

\(\begin{array}{l} A × B \end {массив} \)

= {

\(\begin{массив}{l} ( a,b):a \in A, b\in B \end{массив} \)

}

Его также называют перекрестным продуктом, набором прямых продуктов или набором продуктов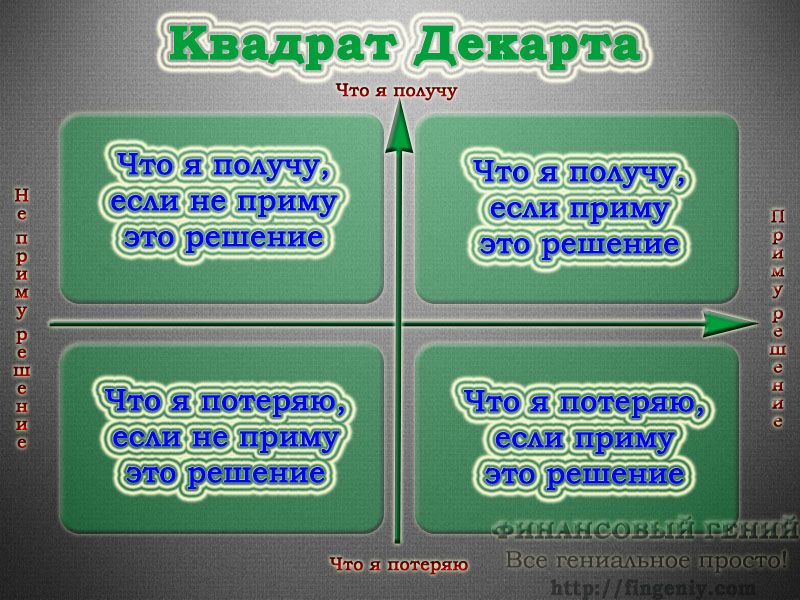

A и 9. 0061 Б .

Подробнее: Типы наборов

Здесь очень важно отметить, что это набор упорядоченных пар. Под упорядоченной парой подразумевается, что два элемента, взятые из каждого набора, записаны в определенном порядке. Итак, если a ≠ b , упорядоченные пары ( a,b ) и (b,a) различны.

Декартова площадь

Если оба множества декартова произведения одинаковы, скажем, множество A = множество B, то декартово произведение множества C и D называется декартовым квадратом.

А = В

A x B = A ² = {(a,b): a ∈ C, b ∈ C}

Декартово произведение пустого набора

Как известно, в пустом множестве нет элементов. Мощность пустого множества или размер также равен нулю. Декартово произведение множества, скажем, A и пустого множества ∅, является только пустым множеством.

А х ∅ = ∅

Свойства декартова произведения

• Декартово произведение некоммутативно. Таким образом, если мы изменим порядок наборов, результат изменится. Если A и B два множества, то декартово произведение A и B, A × B ≠ B × A
• Декартово произведение не ассоциативно. Если мы перегруппируем множества в декартовом произведении, то это изменит результат. Если A, B и C — три множества, то (A × B) × C ≠ A × (B × C)
.
• Свойство распределения декартова произведения на пересечении множеств определяется как A × (B ∩ C) = (A × B) ∩ (A × C)
• Свойство распределения декартова произведения по объединению множеств определяется как A × (B∪C) = (A × B) ∪ (A × C)
• Результатом декартова произведения множеств является множество всех упорядоченных пар

Декартово произведение и упорядоченные пары Решаемые примеры

Пример 1:

Для примера возьмем P в качестве набора оценок в школе из набора Q в качестве разделов для оценок. Итак, у нас есть

P и Q как:

\(\begin{массив}{l}~~~~~~~~~~~~~~~~~~~\end{массив} \)

P = {8,9,10}

\(\begin{array}{l}~~~~~~~~~~~~~~~~~~~\end{array} \)

Q = {A,B,C,D }

Итак,

\(\begin{array}{l} P × Q \end{array} \)

, по определению будет равно,

\(\begin{array}{l} P × Q \end{массив} \)

= { (8 ,A ) , (8 ,B ) , (8 ,C ) , (8 ,Д ),(9 ,А ) , (9 ,Б ),(9 ,С ),(9 ,Д ),(9 ,Д А ),(10 ,В ),(10 ,с ),(10, Д )}

Всего заказано 12 пар.

Если n ( P ) и n ( Q ) представляют количество элементов в наборах P и Q соответственно, тогда n ( P ) = 0 ( P ) Q ) =4. Итак, n(P×Q ) = 3 × 4 = 12. См. рисунок 1, где показано то же самое. На рисунке хорошо видно, как

\(\begin{array}{l} P × Q \end{array} \)

образует плоскость, также называемую декартовой плоскостью. Каждая точка представляет собой упорядоченную пару, которая имеет первый элемент из набора P и второй элемент из набора Q . Если количество элементов в множестве A и B равно p и q соответственно, то количество элементов в декартовом произведении множеств будет pq , т.е.

Если n ( A ) = p и n ( B ) = q и , то n ( A × B ) = pq .

Из этого свойства можно сделать два вывода:

Рисунок 1: Изображение всех возможных упорядоченных пар для

\(\begin{array}{l} P × Q \end{array} \)

Пример 2:

Чтобы две упорядоченные пары были равны, их соответствующие элементы должны быть равны. Например. Если упорядоченные пары (9,13) и (x+3, y+6) равны,

\(\begin{array}{l}~~~~~~~~~~~~~~~~~~~\end{array} \)

x + 3 = 9 ⇒ x = 6

\(\begin{array}{l}~~~~~~~~~~~~~~~~~~~~\end{array} \)

y + 6 = 13 ⇒ y = 7

Факты о декартовом произведении

• Декартово произведение множеств не ограничивается только двумя множествами. Это также справедливо для более чем двух сетов. Но сложность увеличивается по мере увеличения количества наборов.
• Для трех наборов A, B и C элемент A × B × C представлен как ( a, b, c ) и называется упорядоченной тройкой.
• Если мы возьмем декартово произведение двух множеств как R × R , где R — набор действительных чисел, представляющий всю двумерную декартову плоскость. Точно так же R × R × R представляет трехмерное декартово пространство.

Декартово произведение в реляционной алгебре

Декартово произведение в реляционной алгебре — это бинарный оператор.