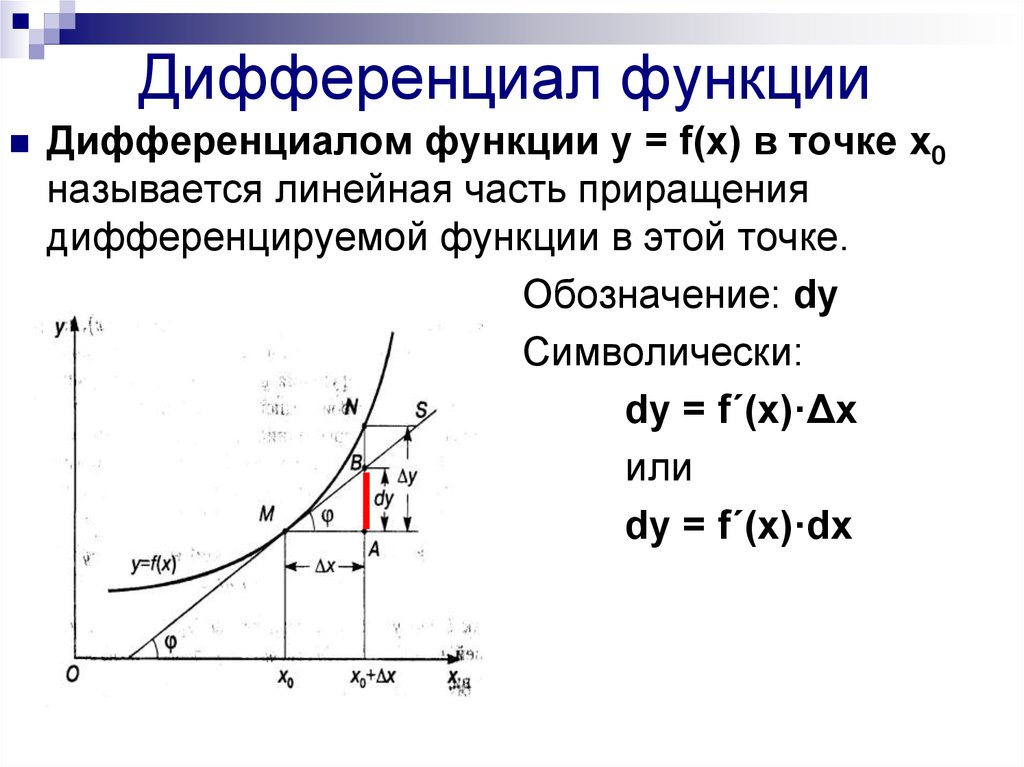
методика «Личностный дифференциал»
методика «Личностный дифференциал»Инструкция Перед вами шкала, на полюсах которой расположены свойства личности. Ваша задача — оценить себя по каждой из шкал, т.е. определить, какое свойство из каждой пары предложенных свойств характерно для вас и в какой степени оно проявляется.
| 3 | 2 | 1 | 0 | 1 | 2 | 3 | |||
| 1 | замкнутый | общительный | |||||||
| 2 | конкретно мыслящий | абстрактно мыслящий | |||||||
| 3 | эмоционально устойчивый | эмоционально не устойчивый | |||||||
| 4 | подчиненный | доминантный | |||||||
| 5 | сдержанный | экспрессивный | |||||||
| 6 | подверженный влиянию чувств | нормативный | |||||||
| 7 | робкий | смелый | |||||||
| 8 | жесткий | чувствительный | |||||||
| 9 | доверчивый | подозрительный | |||||||
| 10 | практичный | творческий | |||||||
| 11 | прямолинейный | дипломатичный | |||||||
| 12 | уверенный в себе | тревожный | |||||||
| 13 | консервативный | радикальный | |||||||
| 14 | зависимый от группы | самостоятельный | |||||||
| 15 | недисциплинированный | дисциплинированный | |||||||
| 16 | расслабленный | напряженный | |||||||

Источник:
|
Семантический дифференциал в режиме онлайн как инструмент исследования семантико-перцептивных универсалий и личностно-смысловых установок
+7 (495) 669-67-19
Заказать звонок
22 Февраля 2012
Печать PDF
Александр Шмелев, HT.RU, впервые опубликовано в сборнике «Психология субъективной семантики: истоки и развитие» (под редакцией И.Б.Ханиной и Д.А.Леонтьева). – Москва: Смысл, 2012, с. 103-118
 Уже первая моя монография (Шмелев, 1983) отчетливо фиксирует иной фокус и предмет применения психосемантических методов, чем это можно увидеть в первой монографии по психологии субъективной семантики Е.Ю. Артемьевой (Артемьева, 1980).
Увлекаясь психометрикой и математическим моделированием субъективных семантических пространств, автор данной статьи в те уже далекие годы с некоторым удивлением наблюдал за тем, как его научный руководитель — профессиональный математик высочайшего класса, владеющий всеми современными методами многомерного анализа данных, — все больше тяготеет к приемам точечного и качественного анализа низкоагрегированных (индивидуальных) результатов скорее, чем к компьютерным расчетам с помощью выделения главных компонент (факторов) и построению высокоагрегированных (интегративных, глобальных) моделей. Об этом автор уже писал в одной из своих статей, посвященных научному творчеству Е.Ю. Артемьевой (Шмелев, 1990). «Почему же, Елена Юрьевна, Вы не пользуетесь возможностями компьютерного факторного анализа?» — спрашивал я своего научного руководителя, предлагая собственные услуги как практического программиста, имеющего редкий в те годы прямой доступ к запуску программ факторного анализа прямо с монитора мини-ЭВМ.
Уже первая моя монография (Шмелев, 1983) отчетливо фиксирует иной фокус и предмет применения психосемантических методов, чем это можно увидеть в первой монографии по психологии субъективной семантики Е.Ю. Артемьевой (Артемьева, 1980).
Увлекаясь психометрикой и математическим моделированием субъективных семантических пространств, автор данной статьи в те уже далекие годы с некоторым удивлением наблюдал за тем, как его научный руководитель — профессиональный математик высочайшего класса, владеющий всеми современными методами многомерного анализа данных, — все больше тяготеет к приемам точечного и качественного анализа низкоагрегированных (индивидуальных) результатов скорее, чем к компьютерным расчетам с помощью выделения главных компонент (факторов) и построению высокоагрегированных (интегративных, глобальных) моделей. Об этом автор уже писал в одной из своих статей, посвященных научному творчеству Е.Ю. Артемьевой (Шмелев, 1990). «Почему же, Елена Юрьевна, Вы не пользуетесь возможностями компьютерного факторного анализа?» — спрашивал я своего научного руководителя, предлагая собственные услуги как практического программиста, имеющего редкий в те годы прямой доступ к запуску программ факторного анализа прямо с монитора мини-ЭВМ.

1) холодный — теплый
2) легкий — тяжелый
3) медленный — быстрый
4) безобразный — красивый
5) мягкий — твердый
6) тихий — шумный
7) горький — сладкий
8) малый — большой
9) вялый — бодрый
10) противный — приятный
11) податливый — упругий
12) тусклый — яркий Шкалы были специально подобраны так, чтобы на каждый фактор приходились ровно по 4 шкалы: на фактор «Оценки» шкалы 1, 4, 7, 10; на фактор «Силы» шкалы 2, 5, 8, 11; на фактор «Активности» шкалы 3, 6, 9 и 12.
 Такая структура подтверждалась неоднократно в русскоязычных исследованиях, проведенных с использованием более обширных наборов шкал и объектов (Петренко, 1983).
В качестве шкалируемых был использован фиксированный набор из шести понятий: Скала, Ручей, Цветок, Наука, Искусство, Психология. Смысл такого подбора шкалируемых понятий был обусловлен поставленными задачами исследования: первые три понятия должны были моделировать в основном пары «физический объект — физический признак», в то время как последние три понятия — пары «абстрактно-социальный объект — метафорический признак». К тому же включение понятия «психология» в ряд с такими понятиями как «наука» и «искусство» позволяет использовать данные этого исследования для измерения личностно-социальных установок студентов в отношении той науки, которую они изучают. То есть, в данном контексте вопрос, связанный с третьей задачей исследования, можно переформулировать так: а к чему ближе «психология» в субъективном семантическом пространстве у студентов-психологов — к понятию «наука» или к понятию «искусство»?
Испытуемые и процедура
В качестве испытуемых в данном исследовании выступили 138 студентов второго курса факультета психологии МГУ, проходившие в 2004 году занятия практикума по «Общей психологии».
Такая структура подтверждалась неоднократно в русскоязычных исследованиях, проведенных с использованием более обширных наборов шкал и объектов (Петренко, 1983).
В качестве шкалируемых был использован фиксированный набор из шести понятий: Скала, Ручей, Цветок, Наука, Искусство, Психология. Смысл такого подбора шкалируемых понятий был обусловлен поставленными задачами исследования: первые три понятия должны были моделировать в основном пары «физический объект — физический признак», в то время как последние три понятия — пары «абстрактно-социальный объект — метафорический признак». К тому же включение понятия «психология» в ряд с такими понятиями как «наука» и «искусство» позволяет использовать данные этого исследования для измерения личностно-социальных установок студентов в отношении той науки, которую они изучают. То есть, в данном контексте вопрос, связанный с третьей задачей исследования, можно переформулировать так: а к чему ближе «психология» в субъективном семантическом пространстве у студентов-психологов — к понятию «наука» или к понятию «искусство»?
Испытуемые и процедура
В качестве испытуемых в данном исследовании выступили 138 студентов второго курса факультета психологии МГУ, проходившие в 2004 году занятия практикума по «Общей психологии». Каждый студент производил шкалирование шести понятий по 12-ти шкалам непосредственно за экраном монитора в компьютерном классе с использованием системы HT-LINE. На рисунке-скриншоте 1 читатель может увидеть, как выглядит экран монитора в ходе процедуры шкалирования. Испытуемый, вооруженный мышкой и клавиатурой, должен выносить свои оценки, устанавливая «точки» в известный и стандартный элемент интерактивности в современных веб-интерфейсах — радио-кнопки.
Каждый студент производил шкалирование шести понятий по 12-ти шкалам непосредственно за экраном монитора в компьютерном классе с использованием системы HT-LINE. На рисунке-скриншоте 1 читатель может увидеть, как выглядит экран монитора в ходе процедуры шкалирования. Испытуемый, вооруженный мышкой и клавиатурой, должен выносить свои оценки, устанавливая «точки» в известный и стандартный элемент интерактивности в современных веб-интерфейсах — радио-кнопки.
Обработка результатов Обработка результатов проведенного исследования производилась с помощью двух главных инструментов: 1) штатных (встроенных) онлайн-процедур обработки результатов шкалирования, присутствующих в каждом «Личном кабинете» в системе HT-LINE: это расчет усредненных шкальных профилей по каждому объекту шкалирования, это построение рейтинга респондентов по убыванию согласованности со шкальными оценками усредненного респондента, это кластерный анализ объектов, шкал и респондентов (по сходству вынесенных оценок) и т.
 п.;
2) с помощью электронной таблицы MS Excel — с целью построения диаграмм в наиболее привычных форматах, а также с целью выполнения особых дополнительных процедур корреляционного анализа для сводных таблиц с результатами. Следует пояснить, что в рамках системы HT-LINE реализован удобный (запускаемый одной кнопкой) режим экспорта куба данных в Excel, где возможна реализация всего многообразия методов анализа и представления результатов, присутствующих в этом самом популярном электронно-статистическом пакете.
Результаты и их анализ
Анализ усредненных оценок
Для проверки диагностической гипотезы исследования в ходе обработки результатов был выполнен подсчет средних факторных значений для всех объектов по всем испытуемым. В таблице 1 Вы можете увидеть эти данные в числовой форме:
п.;
2) с помощью электронной таблицы MS Excel — с целью построения диаграмм в наиболее привычных форматах, а также с целью выполнения особых дополнительных процедур корреляционного анализа для сводных таблиц с результатами. Следует пояснить, что в рамках системы HT-LINE реализован удобный (запускаемый одной кнопкой) режим экспорта куба данных в Excel, где возможна реализация всего многообразия методов анализа и представления результатов, присутствующих в этом самом популярном электронно-статистическом пакете.
Результаты и их анализ
Анализ усредненных оценок
Для проверки диагностической гипотезы исследования в ходе обработки результатов был выполнен подсчет средних факторных значений для всех объектов по всем испытуемым. В таблице 1 Вы можете увидеть эти данные в числовой форме:
Для большей наглядности на рисунках 2а, 2б и 3 приводятся гистограммы, по которым можно сравнить, каким образом оценки разных объектов (шкалируемых понятий) отличаются между собой по отдельным шкалам и в целом по факторам.

Интересную и поучительную визуализацию взаимного расположения понятий дает нам на рисунке 4 геометрическая модель EPA в двухфакторной проекции на первые 2 факторные шкалы (оси) — Оценка и Сила. Из этой модели видно, что «психология» по сравнению с «наукой» воспринимается студентами второго курса как более «приятный объект», но… «менее сильный». Также видно, что от точки, локализующей в этом пространстве понятие «психология», до точки «искусство» расстояние оказывается почти в 2 раза более коротким, чем до точки «наука».
Теперь используем такой прием в представлении данных, который использовала в своих работах Е.Ю. Артемьева, — построение «качественного семантического кода» для шкалируемых объектов. Этот прием означает применение некоторого статистически обоснованного порога (по числу совпадения ассоциаций у разных испытуемых), ниже которого все связи между тем или иным полюсом шкалы и объектом признаются незначимыми, то есть, нулевым. Но, как мы хорошо знаем из статистики, для разных уровней статистической значимости можно выбирать разные пороги.
 Поэтому мы в нашей работе применили несколько разных порогов и проследили различия в «семантических кодах» (семантических полях), возникающих при этом.
Поэтому мы в нашей работе применили несколько разных порогов и проследили различия в «семантических кодах» (семантических полях), возникающих при этом.
В таблице 3а можно увидеть, как происходит обнуление тех значений из таблицы 1, которые оказались ниже порога 0,2. А в таблице 3б можно увидеть, как происходит обнуление тех значений из таблицы 1, которые оказались ниже порога 0,8. Из каждой таблицы теперь мы легко на основе простого перечисления строим «качественную модель семантического поля» каждого из шести объектов, а именно — путем перечисления шкальных полюсов, имеющих значение 1 по модулю. Получаем два смысловых поля («семантических кода») для интересующего нас понятия «психология»: Для порога 0,8 этот код для понятия «психология» содержит только три слова-прилагательных: «красивый + большой + приятный». Для порога 0,2 этот код для того же слова «психология» значительно шире и содержит 9 прилагательных: «теплый + тяжелый + красивый + мягкий + большой + бодрый + приятный + податливый + яркий».
 Теперь для этих качественных данных мы можем применить метрику сходства семантических (ассоциативных) полей, которая, в частности, обоснована в работе американского психолингвиста Джейма Диза как «коэффициент пересечения» (intersection coefficient — см. Deese, 1970), которая является частным случаем коэффициента конгруэнтности для номинативных (качественных) признаков:
Теперь для этих качественных данных мы можем применить метрику сходства семантических (ассоциативных) полей, которая, в частности, обоснована в работе американского психолингвиста Джейма Диза как «коэффициент пересечения» (intersection coefficient — см. Deese, 1970), которая является частным случаем коэффициента конгруэнтности для номинативных (качественных) признаков:
где Аik — оценка объекта i по шкале k, ?— суммирование по всем шкалам (то есть, индекс K пробегает все N значений по числу шкал). Чтобы читателю было легко следить за ходом подсчетов, приведем пример вычисления коэффициента пересечения для семантических полей «скала» и «психология» из таблиц 3а и 3б. В таблице 3а, по трем шкалам коды для «скалы» и «психологии» совпадают (оба объекта «красивые, большие и приятные), а по двум шкалам полюса оказываются противоположными («скала» вызывает ассоциации с «холодным и твердым», а «психология — с «теплым и мягким»). Суммы квадратов по каждому столбцу совпадают с числом клеток, отличных от нуля: для «скалы» это значение 10, а для «психологии» — 9.
 Поэтому IC оказывается равным:
IC = (3–2) / ? (10 * 9) = 0,11
В таблице 3б, по трем шкалам коды для «скалы» и «психологии» совпадают (оба объекта «красивые, большие и приятные), а вот те шкалы, по которым у «скалы» и «психологии» полюса оказывались противоположными, при этом высоком пороге получили нулевые значения (не входят в область пересечения семантических полей). Суммы квадратов по каждому столбцу в этом случае оказываются равными 8 и 3 соответственно. Поэтому IC оказывается равным:
IC = 3 / ? (8 * 3) = 0,61
Вот как, оказывается, резко зависит семантическая близость понятий от выбора того или иного «порога отсечения»! Для каких-то пар понятий при изменении порога близость может повышаться, а для каких-то, наоборот, понижается.
Даже не создавая никаких особенных программ для компьютера, используя только современные электронные таблицы (которых, увы, просто не было в те времена в распоряжении Елены Юрьевны), мы легко можем проследить определенные закономерности, рассчитав близости одного понятия со всеми другими в нашем эксперименте на фоне изменения «порога отсечения».
Поэтому IC оказывается равным:
IC = (3–2) / ? (10 * 9) = 0,11
В таблице 3б, по трем шкалам коды для «скалы» и «психологии» совпадают (оба объекта «красивые, большие и приятные), а вот те шкалы, по которым у «скалы» и «психологии» полюса оказывались противоположными, при этом высоком пороге получили нулевые значения (не входят в область пересечения семантических полей). Суммы квадратов по каждому столбцу в этом случае оказываются равными 8 и 3 соответственно. Поэтому IC оказывается равным:
IC = 3 / ? (8 * 3) = 0,61
Вот как, оказывается, резко зависит семантическая близость понятий от выбора того или иного «порога отсечения»! Для каких-то пар понятий при изменении порога близость может повышаться, а для каких-то, наоборот, понижается.
Даже не создавая никаких особенных программ для компьютера, используя только современные электронные таблицы (которых, увы, просто не было в те времена в распоряжении Елены Юрьевны), мы легко можем проследить определенные закономерности, рассчитав близости одного понятия со всеми другими в нашем эксперименте на фоне изменения «порога отсечения». Я уверен, что будь в руках Елены Юрьевны подобный инструментарий, который доступен теперь каждому студенту на любом компьютере (включая портативные нетбуки!), мы сегодня бы уже имели «семантико-перцептивные универсалии» (или «семантические коды») для многих и многих интересных классов стимулов.
В таблице 4 Вы можете увидеть, как меняется «коэффициент пересечения» у понятия «психология» с другими пятью понятиями при разных значениях «порога отсечения» (ПО). Визуализировать определенные закономерности помогает рисунок-гистограмма 5.
Я уверен, что будь в руках Елены Юрьевны подобный инструментарий, который доступен теперь каждому студенту на любом компьютере (включая портативные нетбуки!), мы сегодня бы уже имели «семантико-перцептивные универсалии» (или «семантические коды») для многих и многих интересных классов стимулов.
В таблице 4 Вы можете увидеть, как меняется «коэффициент пересечения» у понятия «психология» с другими пятью понятиями при разных значениях «порога отсечения» (ПО). Визуализировать определенные закономерности помогает рисунок-гистограмма 5.
Итак, что мы наблюдаем? — При любом уровне порога отсечения самым близким понятием к «психологии» оказывается «искусство». И это не противоречит тем результатам, которые мы получили, при расчете евклидова расстояния для высокоинтегративной факторной модели. Но… иерархия остальных понятий по степени их близости к «психологии» в зависимости от порога меняется и весьма существенно! При высоком значении ПО=0,8 на второе место выходит вовсе не «наука» (как это мы видим в модели расстояний), а понятие «скала» (?!).
 Почему? — Легко увидеть, что это происходит из-за того, что более бедное (по составу признаков) семантическое поле «психология» при высоком пороге, как раз не включает в своей состав те признаки, по которым «скала» и «психология» различаются, и не включает, опять-таки, те признаки, по которым оказываются сходными «психология» и «наука» (конкретно это прилагательные «тяжелый и яркий» — сравните таблицы 3а и 3б).
Почему? — Легко увидеть, что это происходит из-за того, что более бедное (по составу признаков) семантическое поле «психология» при высоком пороге, как раз не включает в своей состав те признаки, по которым «скала» и «психология» различаются, и не включает, опять-таки, те признаки, по которым оказываются сходными «психология» и «наука» (конкретно это прилагательные «тяжелый и яркий» — сравните таблицы 3а и 3б).
Так что оказывается, что в зависимости от выбора «порога отсечения», мы получаем существенно разные низкоинтегративные модели семантического поля объекта (качественные, пошкальные, а не пофакторные): при понижении порога близость ко всем физическим объектам у понятия «психология» сокращается, а близость ко всем «абстрактным понятиям» — растет (или сокращается, но в относительно меньшей степени). На уровне самого низкого порога ПО=0,2 мы получаем точно такую же иерархию отношений близости как для «евклидова» расстояния. Таким образом, по нашим данным прослеживается следующая закономерность: высокопороговые низкоинтегративные психосемантические (эмпирические) модели значения слова оказываются, в большей степени, насыщены коннотативными (эмоционально-оценочными) компонентами, которые при суммировании результатов, полученных от разных испытуемых, оказываются в некотором смысле константными, то есть, получают статус неких «семантических универсалий».
 В то же время, низкопороговые низкоинтегративные модели уже вбирают в себя ряд денотативных (предметно-отнесенных, буквальных) компонентов значения слова.
Стремясь получить устойчивые семантико-перцептивные универсалии, в своих экспериментах Е.Ю. Артемьева работала, как правило, с высокопороговыми и низкоинтегративными моделями значения. Такой ее методический подход был вполне адекватен тем исследовательским целям и задачам, которые она перед собой ставила.
Анализ дисперсий по шкалам
Для того, чтобы проверить гипотезу о связи между метафоричностью шкал и дисперсией, мы рассчитали дисперсию индивидуальных оценок для каждой пары «объект—шкала». За каждой клеточкой таблицы 5 скрываются 138 различных индивидуальных оценок. Их разброс отражает, как известно, такую меру рассеяния как среднее квадратичное отклонение, которое каждый читатель (и студент практикума) легко может посчитать с помощью стандартной функции в электронной таблице MS Excel.
В то же время, низкопороговые низкоинтегративные модели уже вбирают в себя ряд денотативных (предметно-отнесенных, буквальных) компонентов значения слова.
Стремясь получить устойчивые семантико-перцептивные универсалии, в своих экспериментах Е.Ю. Артемьева работала, как правило, с высокопороговыми и низкоинтегративными моделями значения. Такой ее методический подход был вполне адекватен тем исследовательским целям и задачам, которые она перед собой ставила.
Анализ дисперсий по шкалам
Для того, чтобы проверить гипотезу о связи между метафоричностью шкал и дисперсией, мы рассчитали дисперсию индивидуальных оценок для каждой пары «объект—шкала». За каждой клеточкой таблицы 5 скрываются 138 различных индивидуальных оценок. Их разброс отражает, как известно, такую меру рассеяния как среднее квадратичное отклонение, которое каждый читатель (и студент практикума) легко может посчитать с помощью стандартной функции в электронной таблице MS Excel.
Жирным шрифтом мы выделили в таблице 5 те пары «объект—шкала», для которых оценивание можно считать «физическим», а не «метафорическим».
 То есть, любой физический объект может быть на вид «ярким или тусклым», на ощупь — «твердым или мягким». Хотя, например, такой физический объект как «ручей» не поднимают на руки, поэтому к нему в физическом смысле не применима шкала «тяжелый — легкий». Равно как к таким статическим объектам как «скала» и «цветок» не применима шкала, имеющая физический смысл лишь в отношении движущихся объектов — «быстрый — медленный». Конечно, даже невооруженным взглядом видно, что в ряде случаев физическое оценивание объекта по физической шкале не дает низкой дисперсии (высокой согласованности между оценщиками-респондентами) не потому, что оно является некорректным или метафорическим (разномодальным), а потому, что каждый индивид актуализирует РАЗЛИЧНЫЙ физический образ одного и того же физического понятия. Понятие «ручей» у одного может актуализировать образ «холодного ручья», а у другого — «теплого ручья». В этом смысле мы должны признать, что в нашем эксперименте шкалированию подвергаются не сами по себе физические объекты (конкретный ручей, или конкретный цветок), а собирательные понятия, которые по-разному могут быть конкретизированы.
То есть, любой физический объект может быть на вид «ярким или тусклым», на ощупь — «твердым или мягким». Хотя, например, такой физический объект как «ручей» не поднимают на руки, поэтому к нему в физическом смысле не применима шкала «тяжелый — легкий». Равно как к таким статическим объектам как «скала» и «цветок» не применима шкала, имеющая физический смысл лишь в отношении движущихся объектов — «быстрый — медленный». Конечно, даже невооруженным взглядом видно, что в ряде случаев физическое оценивание объекта по физической шкале не дает низкой дисперсии (высокой согласованности между оценщиками-респондентами) не потому, что оно является некорректным или метафорическим (разномодальным), а потому, что каждый индивид актуализирует РАЗЛИЧНЫЙ физический образ одного и того же физического понятия. Понятие «ручей» у одного может актуализировать образ «холодного ручья», а у другого — «теплого ручья». В этом смысле мы должны признать, что в нашем эксперименте шкалированию подвергаются не сами по себе физические объекты (конкретный ручей, или конкретный цветок), а собирательные понятия, которые по-разному могут быть конкретизированы.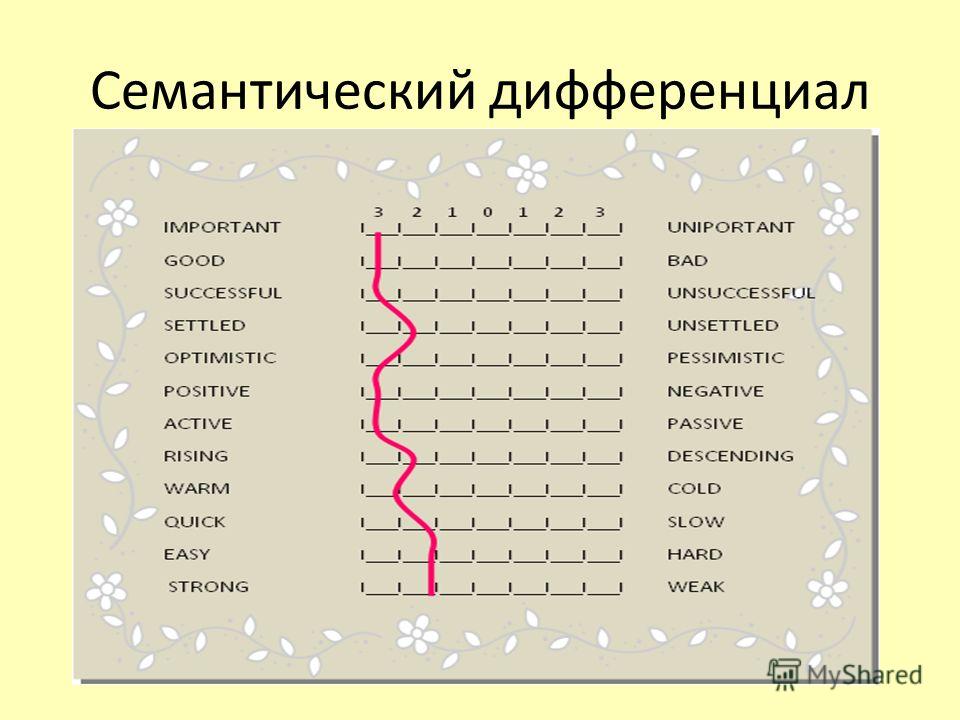 Но все-таки мы видим, что большинство чисел, выделенных в таблице 5, оказывается ниже некоторого среднего значения для этой таблицы (оно равно 1,05). Если быть совсем точными, то в 11 случаях из 15 мы наблюдаем более низкие значения, чем среднее значение 1,05. Это отклонение от ожидаемого среднего 7,5 (половина случаев) не является статистически значимым, но легко себе представить более масштабный эксперимент с большим числом физических понятий, который, конечно, дал бы нам значимый статистический результат в этом направлении — в направлении подтверждения выдвинутой гипотезы.
На базе таблицы 5 с помощью стандартной функции MS Excel под названием «Ранг» была построена таблица 6. В каждой клетке таблицы 6 стоит ранг от 1 до 6, указывающей на место данной пары «объект—шкала» в ряду возрастающих значений по данной шкале (1 — минимальное значение стандартного отклонения).
Но все-таки мы видим, что большинство чисел, выделенных в таблице 5, оказывается ниже некоторого среднего значения для этой таблицы (оно равно 1,05). Если быть совсем точными, то в 11 случаях из 15 мы наблюдаем более низкие значения, чем среднее значение 1,05. Это отклонение от ожидаемого среднего 7,5 (половина случаев) не является статистически значимым, но легко себе представить более масштабный эксперимент с большим числом физических понятий, который, конечно, дал бы нам значимый статистический результат в этом направлении — в направлении подтверждения выдвинутой гипотезы.
На базе таблицы 5 с помощью стандартной функции MS Excel под названием «Ранг» была построена таблица 6. В каждой клетке таблицы 6 стоит ранг от 1 до 6, указывающей на место данной пары «объект—шкала» в ряду возрастающих значений по данной шкале (1 — минимальное значение стандартного отклонения).
Не требуется даже применять особые критерии непараметрической статистики (вроде «разности ранговых сумм» — Рунион, 1982) , чтобы увидеть, что сумма рангов по первым трем столбцам меньше, чем сумма рангов по последним трем столбцам.
 Обсуждение результатов и выводы
Итак, в нашем эксперименте мы описали методику и результаты, полученные с помощью онлайн-системы проведения методики «семантического дифференциала». Этот инструментарий очень удобен и для учебных, и для исследовательских целей, так как многократно ускоряет процессы проектирования подобных методик и сбора массовых результатов.
Наши результаты свидетельствуют в пользу выдвинутых нами гипотез, и решают поставленные задачи исследования:
1) Метафорическое применение шкал «семантического дифференциала» дает больший разброс (дисперсию) индивидуальных оценок, что говорит о большем психодиагностическом потенциале методики СД именно в случае метафорического оценивания с помощью шкал СД абстрактных понятий, а не конкретных физических объектов;
2) Студенты-психологи воспринимают понятие «психология» как более близкое к понятию «искусство», чем к понятию «наука», что, соответствуя другим, неформализованным наблюдениям, служит одновременно подтверждением валидности тех измерений личностно-смысловых установок, которые можно производить с помощью метода «семантического дифференциала».
Обсуждение результатов и выводы
Итак, в нашем эксперименте мы описали методику и результаты, полученные с помощью онлайн-системы проведения методики «семантического дифференциала». Этот инструментарий очень удобен и для учебных, и для исследовательских целей, так как многократно ускоряет процессы проектирования подобных методик и сбора массовых результатов.
Наши результаты свидетельствуют в пользу выдвинутых нами гипотез, и решают поставленные задачи исследования:
1) Метафорическое применение шкал «семантического дифференциала» дает больший разброс (дисперсию) индивидуальных оценок, что говорит о большем психодиагностическом потенциале методики СД именно в случае метафорического оценивания с помощью шкал СД абстрактных понятий, а не конкретных физических объектов;
2) Студенты-психологи воспринимают понятие «психология» как более близкое к понятию «искусство», чем к понятию «наука», что, соответствуя другим, неформализованным наблюдениям, служит одновременно подтверждением валидности тех измерений личностно-смысловых установок, которые можно производить с помощью метода «семантического дифференциала». Новым и несколько неожиданным результатом нашего исследования оказалось выявление следующей закономерности в выборе «порога отсечения» — при формировании «семантического кода» шкалируемых объектов с помощью того приема, который использовала Е.Ю. Артемьева. Оказывается, высокие пороги отсечения нам дают более «коннотативные» (эмоционально окрашенные) коды, а более низкие пороги — больше моделируют предметную отнесенность значения. Дальнейшая перспектива подобных исследований состоит в том, чтобы изучить, в какой мере индивидуальные различия между испытуемыми в их способах категоризации и построения семантического «образа мира» можно моделировать с помощью «порога отсечения».
Литература
Артемьева Е.Ю. Психология субъективной семантики. М.: Изд-во Моск. ун-та, 1980.
Новым и несколько неожиданным результатом нашего исследования оказалось выявление следующей закономерности в выборе «порога отсечения» — при формировании «семантического кода» шкалируемых объектов с помощью того приема, который использовала Е.Ю. Артемьева. Оказывается, высокие пороги отсечения нам дают более «коннотативные» (эмоционально окрашенные) коды, а более низкие пороги — больше моделируют предметную отнесенность значения. Дальнейшая перспектива подобных исследований состоит в том, чтобы изучить, в какой мере индивидуальные различия между испытуемыми в их способах категоризации и построения семантического «образа мира» можно моделировать с помощью «порога отсечения».
Литература
Артемьева Е.Ю. Психология субъективной семантики. М.: Изд-во Моск. ун-та, 1980.
Петренко В.Ф. Введение в экспериментальную психосемантику: исследование форм репрезентации в обыденном сознании. М.: Изд-во Моск. ун-та, 1983. Практикум по психологии / Под ред.
 А.Н. Леонтьева, Ю.Б. Гиппенрейтер. М.: Изд-во Моск. ун-та, 1972.
А.Н. Леонтьева, Ю.Б. Гиппенрейтер. М.: Изд-во Моск. ун-та, 1972.
Рунион Р. Справочник по непараметрической статистике: Современный подход. – М.: Финансы и статистик, 1982.
Шмелев А.Г. Введение в экспериментальную психосемантику: теоретико-методологические основания и психодиагностические возможности. М.: Изд-во Моск. ун-та, 1983.
Шмелев А.Г. Семантический код и возможности матричной психодиагностики // Вестн. Моск. ун-та. Серия 14. Психология. 1990. № 3. С. 23–28.
Deese J. Psycholingistics. Boston: Allyn and Bacon, 1970.
Новые статьи и исследования
В вашей почте раз в неделю. А еще: новости, акции и мероприятия для HR.
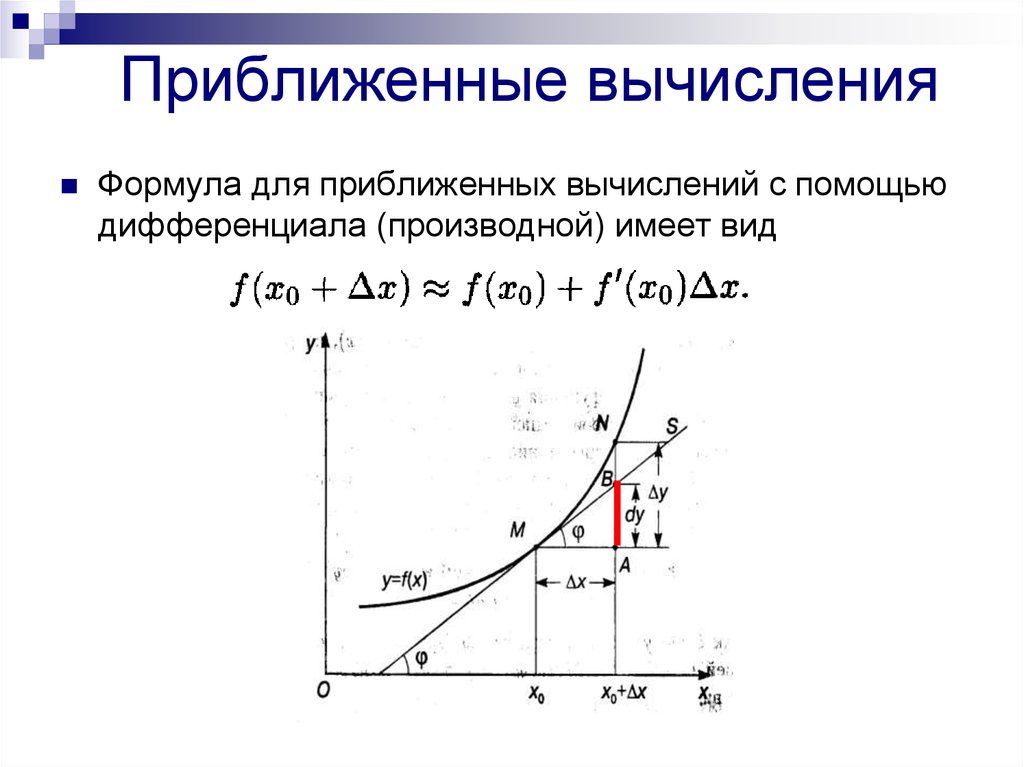
Дифференциальные уравнения — Онлайн-портфолио семинара для старших
Снова возвращаясь к исчислению, вспомним неявное дифференцирование, которое включало попытку дифференцировать уравнение, содержащее более одной переменной. Напомним, что мы обозначаем первую производную для дифференциальных уравнений как . Где мы берем производную по времени. Мы можем применить это к любой переменной, однако основное внимание уделяется тому, чтобы проиллюстрировать изменение над изменением в . Чтобы вычислить это, нам нужно найти предел по мере приближения. Поскольку мы не можем напрямую заменить, нам нужно вычислить значения для изменения, близкие к . Это позволит нам аппроксимировать предел из [16]. Мы находим формулу, сначала признавая, что где
Где мы берем производную по времени. Мы можем применить это к любой переменной, однако основное внимание уделяется тому, чтобы проиллюстрировать изменение над изменением в . Чтобы вычислить это, нам нужно найти предел по мере приближения. Поскольку мы не можем напрямую заменить, нам нужно вычислить значения для изменения, близкие к . Это позволит нам аппроксимировать предел из [16]. Мы находим формулу, сначала признавая, что где
Определим эту формулу как метод Эйлера. Здесь мы видим, что формула состоит в том, чтобы вычислить значение текущего шага, используя предыдущее значение, аналогично идее в методах Ньютона-Рафсона и Секанта. Мы также можем использовать другой массив переменных, чтобы соответствовать формуле, как мы видим в нашем следующем примере.
Рассмотрим уравнение . Учитывая и , вычислить и по методу Эйлера. Сравните с точным решением [15].
Сначала нам нужно записать формулу Эйлера, поскольку она подходит для нашей задачи с информацией, которую мы получили до сих пор.
Мы знаем, что таким образом у нас есть следующие вычисления:
Теперь, когда мы нашли значения для и нам нужно сравнить их с точным решением .
Теперь, чтобы сравнить наши вычисления, мы найдем истинную ошибку для каждого из них.
Из этого примера видно, что хотя аппроксимации близки, нам потребуется еще несколько итераций, прежде чем мы начнем видеть все меньшие и меньшие ошибки, которые означают, что аппроксимации приближаются к точным решениям.
Существует пересмотренная версия метода Эйлера, называемая улучшенным методом Эйлера или методом Хойна.
31.1 Усовершенствованный метод Эйлера
Как упоминалось ранее, улучшенный метод Эйлера представляет собой пересмотренную версию исходной формулы, но с двухэтапным процессом для каждого расчета, который мы выполняли для исходного метода Эйлера. Мы изменили обозначение, чтобы лучше понять задействованные итерации. Пусть будет предыдущее известное значение и пусть будет грубым приближением для текущего значения, используемого для аппроксимации конечного значения, . Мы определяем два шага, используя те же переменные, что и для метода Эйлера, следующим образом.
Пусть будет предыдущее известное значение и пусть будет грубым приближением для текущего значения, используемого для аппроксимации конечного значения, . Мы определяем два шага, используя те же переменные, что и для метода Эйлера, следующим образом.
Используя предыдущий пример, который мы использовали для метода Эйлера, мы теперь можем применить улучшенный метод Эйлера.
Рассмотрим уравнение . Учитывая и , вычислить и с помощью усовершенствованного метода Эйлера. Сравните с точным решением [15].
Мы определяем наши два шага для этой задачи следующим образом:
Где , мы можем вычислить и начиная с .
Далее вычисляем.
Теперь мы вычисляем истинную ошибку между точными значениями, которые мы уже нашли в предыдущем примере, и значениями, округленными до 6-й значащей цифры, найденными с помощью улучшенного метода Эйлера.
Это гораздо более низкие истинные ошибки, чем те, которые мы нашли с помощью метода Эйлера. Глядя на сравнение ошибок, мы можем сказать, что усовершенствованный метод Эйлера действительно улучшает приближения по сравнению с истинными значениями.
Глядя на сравнение ошибок, мы можем сказать, что усовершенствованный метод Эйлера действительно улучшает приближения по сравнению с истинными значениями.
Теперь есть третий метод, основанный на усовершенствованном методе Эйлера для получения приближений с еще большей точностью. В следующем подразделе мы узнаем, как использовать метод Рунге-Кутты четвертого порядка для аппроксимации дифференциальных уравнений.
31.2 Метод Рунге-Кутты
Из названия можно сделать вывод, что метод Рунге-Кутты четвертого порядка требует 4 шагов для вычисления одного приближения. Метод Рунге-Кутта считается тем более совершенным, чем больше он имеет наибольшего порядка. Метод Эйлера был первым порядком, и для приближения требовалось всего одно вычисление. Усовершенствованный метод Эйлера был вторым порядком, так как для приближения требовалось 2 подвычисления. Метод Рунге-Кутты относится к методу четвертого порядка, поскольку для его приближения требуется 4 вычисления. Определим формулу для метода Рунге-Кутты четвертого порядка следующим образом [16].
Определим формулу для метода Рунге-Кутты четвертого порядка следующим образом [16].
Мы определяем вычисления, обозначенные следующим образом:
Используя тот же пример, который мы использовали в этом разделе, давайте посмотрим, действительно ли метод Рунге-Кутты четвертого порядка улучшает метод Эйлера и улучшает приближение Эйлера.
Рассмотрим уравнение . Учитывая и , вычислить с помощью метода Рунге-Кутты четвертого порядка. Сравните с точным решением [15].
Начнем с вычисления .
Теперь, когда мы нашли наши значения для , мы можем ввести наши известные значения в нашу формулу и решить для .
Мы вычисляем истинную ошибку этого приближения, используя точное значение, которое мы нашли ранее.
Мы не выполняем расчет для в этом примере, потому что только при вычислении истинной ошибки приближения Рунге-Кутты четвертого порядка для мы видим чрезвычайное улучшение.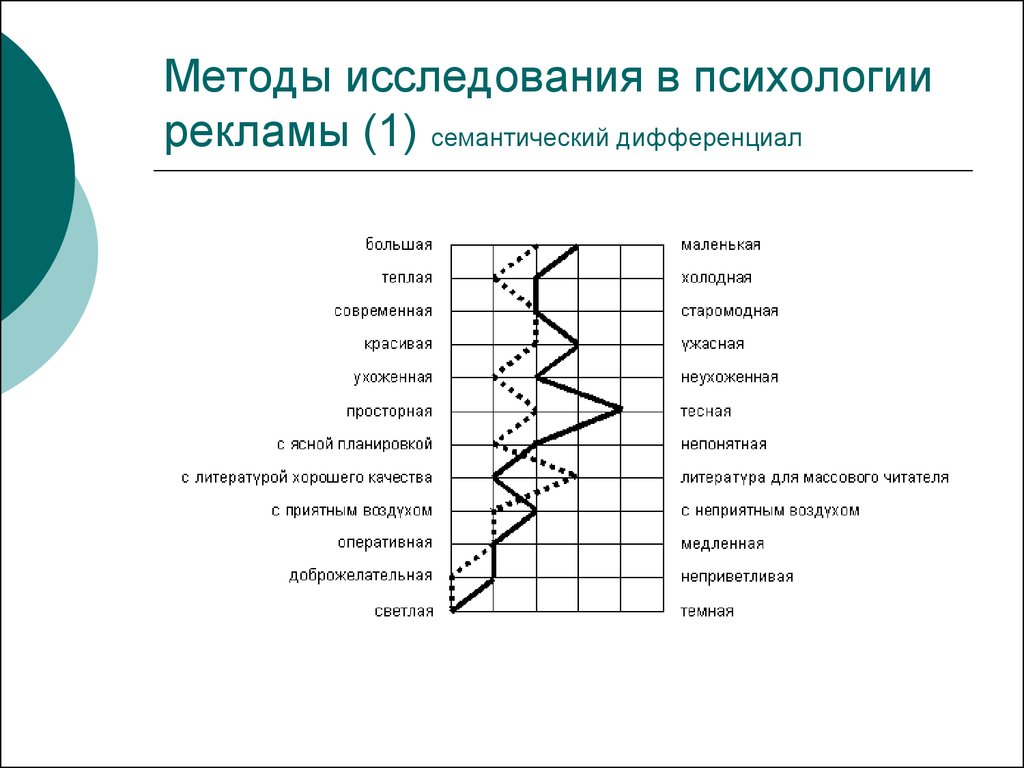 Эта новая истинная ошибка даже меньше той, которую мы нашли для наших аппроксимаций с помощью улучшенного метода Эйлера. Просто из сравнения этих примеров мы можем увидеть прогресс приближения в зависимости от метода, который вы используете для приближения.
Эта новая истинная ошибка даже меньше той, которую мы нашли для наших аппроксимаций с помощью улучшенного метода Эйлера. Просто из сравнения этих примеров мы можем увидеть прогресс приближения в зависимости от метода, который вы используете для приближения.
дифференциальных уравнений для инженеров | Coursera
Об этом курсе
48 140 недавних просмотров
Этот курс посвящен дифференциальным уравнениям и охватывает как теорию, так и приложения. В течение первых пяти недель студенты изучают обыкновенные дифференциальные уравнения, а последняя неделя представляет собой введение в уравнения в частных производных.
Гибкие срокиГибкие сроки
Сброс сроков в соответствии с вашим графиком.
Совместно используемый сертификатСовместно используемый сертификат
Получите сертификат по завершении
100% онлайн100% онлайн
Начните немедленно и учитесь по своему собственному графику.
Coursera LabsCoursera Labs
Включает практические учебные проекты.
Узнайте больше о Coursera Labs Внешняя ссылкаСпециализацияКурс 2 из 5 в
Математика для инженеров Специализация
Начальный уровеньНачальный уровень
Знание исчисления одной переменной.
Часов на выполнениеПрибл. 27 часов
Доступные языкиАнглийский
Субтитры: арабский, французский, португальский (европейский), итальянский, вьетнамский, немецкий, русский, английский, испанский
Чему вы научитесь
Гибкие срокиГибкие сроки
Сбросить сроки в соответствии с вашим графиком.
Совместно используемый сертификат
Получите сертификат по завершении
100 % онлайн100 % онлайн
Начните немедленно и учитесь по собственному графику.
Coursera LabsCoursera Labs
Включает практические учебные проекты.
Узнайте больше о Coursera Labs Внешняя ссылкаСпециализацияКурс 2 из 5 в специализации
Математика для инженеров
Начальный уровеньНачальный уровень
Знание исчисления с одной переменной.
Количество часов на выполнениеПрибл. 27 часов
Доступные языкиАнглийский
Субтитры: арабский, французский, португальский (европейский), итальянский, вьетнамский, немецкий, русский, английский, испанский
Instructor
Jeffrey R. Chasnov
Top Instructor
Профессор
Кафедра математики
170 566 Учащиеся
16 Курсы
Предлагает
The Hong Kong University of Science and Technology
HKUST — динамичный международный исследовательский университет, который неустанно стремится к совершенству, продвигает вперед науку и технологии и обучает новое поколение лидеров Азии и всего мира.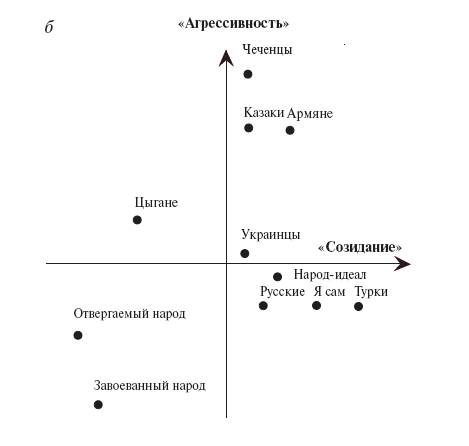
Обзоры
4.9
Заполненные звезды Звездных звездных звезд536 Обзоры
5 Звезды
88,68%
4 Звезды
4 ЗВЕЗДА
%40,70%
3 звезды
1,19%
2 Звезды
0,05%
1 Звездный
0,36%
444. Star
от PDA 15 апреля 2022 г.
Это был очень хороший курс! Я использовал его, чтобы освежить свои знания, а не учиться с нуля, но я думаю, что он в хорошем темпе, а конспекты лекций превосходны! Большое спасибо!
Filled StarFilled StarFilled StarFilled StarFilled Starот JJ 25 мая 2020 г.
У меня нет математического или инженерного образования, но этот курс представляет собой отличный баланс между простотой и сложными задачами, которые я могу с уверенностью использовать для более высокого уровня математики
Filled StarFilled StarFilled StarFilled StarFilled Star от KJ20 мая 2020 г.
Курс понравился. Содержание является точным и объясняет практические приложения, в которых используются дифференциальные уравнения, что делает курс более интересным.
Filled StarFilled StarFilled StarFilled StarFilled Starby AMApr 12, 2021
Отличный курс, который читает отличный профессор, доктор Часнов.
Только правильное содержание, только правильный темп, практические задачи и викторины очень хорошо дополняли материал курса.
Просмотреть все отзывы
О специальности «Математика для инженеров»
Эта специализация была разработана для студентов инженерных специальностей для самостоятельного изучения инженерной математики. Мы ожидаем, что учащиеся уже знакомы с вычислениями с одной переменной и компьютерным программированием. Благодаря этой специализации студенты изучат матричную алгебру, дифференциальные уравнения, векторное исчисление, численные методы и программирование MATLAB. Это даст им инструменты для эффективного применения математики к инженерным задачам и будет хорошо подготовлено для получения степени инженера.
 Скачать конспект лекций по ссылке
https://www.math.hkust.edu.hk/~machas/дифференциальные уравнения-для-инженеров.pdf
Посмотреть рекламный ролик по ссылке
https://youtu.be/eSty7oo09ZI
Скачать конспект лекций по ссылке
https://www.math.hkust.edu.hk/~machas/дифференциальные уравнения-для-инженеров.pdf
Посмотреть рекламный ролик по ссылке
https://youtu.be/eSty7oo09ZI