Прогрессивные матрицы Равена — Блог Викиум
Прогрессивные матрицы Равена или, как их еще называют, тест Равена, это методика, которая позволяет оценить уровень логичности мышления (IQ). Тест появился в 1936 году. Его изобретатели — Л. Пенроуз и Дж. Равен.
Тест основан на традициях английской школы, суть его заключается в выявлении отношений между различными абстрактными фигурами.
Особенной популярностью пользуются два стандартных варианта теста: цветной и черно-белый. Вариант тестирования выбирается в зависимости от возраста тестируемых. Так, цветные тесты предназначены для детей в возрасте от 6 до 9 лет или для пожилых людей в возрасте за 65 лет. В последнем случае тест Равена рекомендуется специалистами в случае необходимости реабилитационных исследований. Может также применяться для детей в возрасте старше 9 лет, если есть подозрение на аномальное развитие.
В основе тестирования лежит гештальт-психология, в частности теория перцепции форм и теория неогенеза, разработанная Ч.
Теория перцепции форм и теория неогенеза
Согласно этой теории испытуемые должны рассматривать задание как единое целое, но состоящее из ряда разнообразных элементов. То есть каждый тестируемый должен изначально оценить задание-матрицу глобально, а уже затем проанализировать его и выделить принцип. Потом из выделенных элементов матрицы формируется целостный образ. В результате должна быть обнаружена недостающая деталь.
Вторая теория, разработанная Спирменом, позволяет более углубленно и детально оценить результаты данного исследования.
Комплекс этих методик и образует тест Равена, который, в свою очередь, отлично согласуется со множеством других подобных методик, например, тестом Векслера и других.
Матрицы Равена могут быть применены для определения интеллектуального развития людей практически любого возраста. При проведении исследований не имеют значения ни социокультурный фон, ни языковой состав, ни степень речевого развития.
Суть методики
Испытуемым выдается по одному стандартному экземпляру тетради, в которой находятся задания, а также один бланк с ответами. Время на выполнение задания строго фиксировано и составляет 35 минут.
Посмотреть тест можно только после того, как будет выдана инструкция по его прохождению, которая озвучивается специалистом.
Специалист выдает матрицы, в которых испытуемые ищут определенный элемент. Процесс происходит следующим образом:
До 5 задания тестируемый может обратиться за подсказкой к экспериментатору. Затем выполняет оставшуюся часть заданий самостоятельно. Экспериментатор обязан сообщить участникам, что выполнять задание нужно как можно скорее и как можно более четко. При необходимости первое задание может быть выполнено даже совместно с экспериментатором. Отсчет времени начинается с момента выполнения пятого задания.
После выполнения все данные будут зафиксированы в бланке ответов.
Главное о методике Равена
Дж. Равен был категорически не согласен с мнением, что интеллект человека закладывается изначально и в дальнейшем не может меняться или каким-то образом преобразовываться.
Он полагал, что интеллект формируется под воздействием не только врожденных качеств человека, но и под воздействием внешних факторов. Именно поэтому он разработал собственный тест, который помогает выявлять и генетические, и средовые причины, которые воздействуют на уровень интеллекта.
В результате разработанный им метод тестирования учитывает только логику человека. При этом уровень образования и другие параметры не имеют значения. Однако учитывается также и скорость принятия решения. Тест может пройти как взрослый человек, так и ребенок.
При обработке данных можно сделать исчерпывающие выводы о пространственном мышлении, особенностях целостного восприятия образов.
Матрица Равена используется в психологии и педагогике уже более полувека, за это время появилось множество вариаций данного метода, однако основной по-прежнему остается самым прогрессивным и востребованным.
Всего в сборнике 60 заданий, которые делятся на 5 серий. Каждая серия включает 12 индивидуальных задач.
Задача тестируемого — определить, как именно связаны между собой фигуры, находящиеся на рисунке, выявить недостающую фигуру и указать на нее. Уровень интеллектуального развития определяется тем, насколько верно и быстро тестируемый справился с заданием. Викиум создал несколько тренажеров на основе данного научного подхода: это «Микросхемы», «Тайная комната», «Геометрия». Узнайте, как работает эта методика уже сегодня!
Прогрессивные матрицы Равена: краткое описание
Тест применяется для диагностики уровня интеллектуального развития испытуемых в возрасте от 8 до 14 лет и от 20 до 65 лет. Тест Равена относится к культурно-инвариантным тестам, так как в минимальной степени показатели по этому тесту зависят от наличия знаний, обусловленных жизнью и определенной культурой.
Материал теста в черно-белом варианте состоит из 60 матриц или композиций
с пропущенным элементом. Задания разделены на пять заданий (А, В, С, Д и Е) по 12 однотипных по возрастающей сложности заданий в каждой серии.
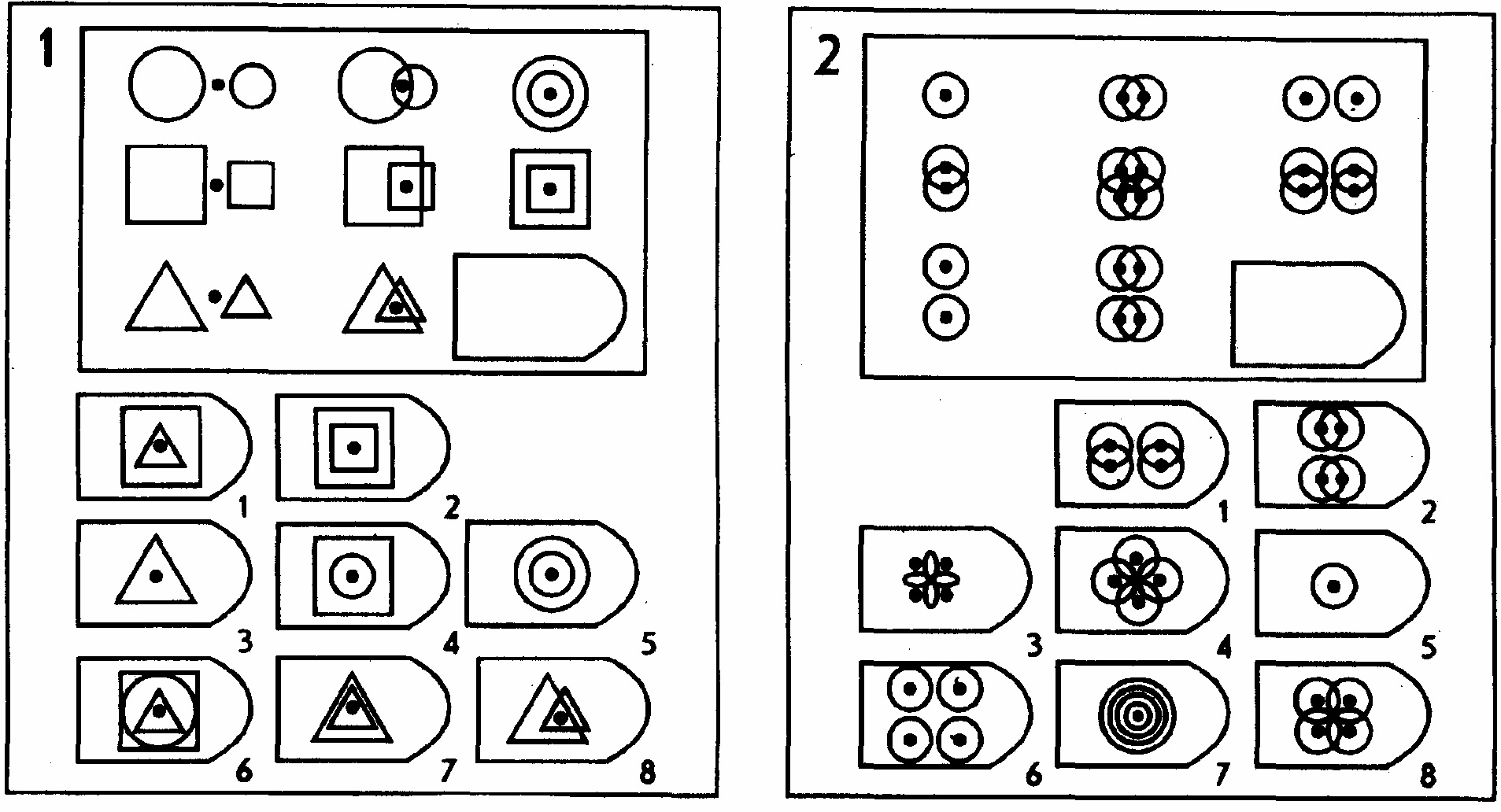
Серия А — диагностируется способность к дифференциации основных элементов структуры и раскрытию связей между ними, идентификации недостающих частей фигуры и сличению ее с представленными образцами (обследуемому необходимо дополнить недостающую часть изображения).
Серия В — оценивается способность к аналогии.
Серия С — диагностируется способность выявлять сложные изменения закономерностей непрерывного развития, обогащения по вертикали и горизонтали.
Серия Д — оценивает способность к пространственной перестановке фигур в матрице по горизонтальному и вертикальному направлениям.
Серия Е — выявляется способность к аналитико-синтетической мыслительной деятельности (задания этой серии включают анализ фигур основного изображения и последующую «сборку» недостающей фигуры по частям).
Обработка полученных результатов заключается в подсчете общего количества баллов, как в отдельной серии, так и в целом по всему тесту.
Тесты для детей
- Анкета «Мотивы выбора друга»
- Анкета по Г. Хорну
- Вопросник-характеристика неуспевающего ученика
- Диагностика периферических нарушений речи у детей
- Диагностическая методика В. М. Когана
- Интервью «Волшебный мир»
- Исследование памяти с помощью методики заучивания десяти слов
- Методика «Аналогии»
- Методика «Аналогии» (версия 2)
- Методика «Вербальная фантазия»
- … и другое
- Диагностика периферических нарушений речи у детей
- Диагностика структуры интеллекта тестом Амтхауэра
- Диагностическая методика «Проблема Эверье»
- Исследование памяти с помощью методики заучивания десяти слов
- КОСКОМ 2
- Корректурная таблица Бентона
- Корректурные пробы
- Культурно-свободный тест на интеллект Р. Кеттелла: краткое описание
- Метод определения яркости и контролируемости представлений путем самооценки (опросник Р.
Гордона) - Метод оценки устойчивости представлений
- … и другое
Гордона)
Метод двойной матрицы — Magoosh GRE
Метод двойной матрицы. В некоторых более сложных комплексных задачах каждый член совокупности классифицируется сразу двумя способами. Например, если бы нам нужно было посмотреть на сотрудников определенной компании, мы могли бы сгруппировать сотрудников по полу, мужчине или женщине. И образование, и здесь мы просто рассмотрим две категории.Только степень бакалавра, т. е. степень бакалавра по сравнению с ученой степенью. В этом примере каждый сотрудник будет классифицирован по полу. Кроме того, каждый сотрудник будет классифицироваться по уровню образования. Таким образом, все будут разделены на две категории одновременно. Информация, которую может дать проблема, может заключаться в том, сколько женщин, и, конечно же, она будет включать оба уровня образования.
Или это может быть количество людей с учеными степенями, и, конечно же, среди них есть как мужчины, так и женщины.
Или это может быть что-то очень конкретное, например, сколько сотрудников — женщины с учеными степенями. Таким образом, вопрос может дать нам любую из этих частей информации. Он также может запросить любую из этих частей информации.
Здесь много информации. Итак, давайте начнем с рассмотрения этого вопроса: в компании из 300 сотрудников 120 женщин. В общей сложности 200 сотрудников имеют ученые степени, а остальные имеют только высшее образование. Если 80 сотрудников — это только мужчины с высшим образованием, сколько женщин с учеными степенями?
Ну, мы пока не собираемся решать эту проблему. Вот что я скажу. Обратите внимание, что некоторые фрагменты информации относительно быстро ведут к другим фрагментам информации. Мы знаем, что есть 300 сотрудников. 120 женщин, а это значит, что остальные 180 должны быть мужчинами.
Аналогично, если 200 сотрудников имеют ученые степени. Ну тогда должно быть 100 человек только с высшим образованием. Так что, безусловно, есть способы, которыми одни части информации ведут к другим, но нам нужен способ организовать всю эту информацию.
Отличный способ организации информации в такой задаче известен как метод двойной матрицы.
Здесь используется матрица, то есть прямоугольный массив ячеек, в каждой из которых есть число. Столбцы будут представлять категории одной переменной, а строки будут представлять категории другой переменной. Для этой задачи предположим, что пол будет столбцами, а уровень образования — строками.
Итак, самое сложное. Есть два пола, поэтому нам понадобятся три столбца. Один для женщин, один для мужчин и один для сумм, мужчин и женщин. Также есть два образовательных уровня, поэтому нам понадобится три ряда. Один только для колледжа, один только для ученой степени и один для итогов. Итак, полная система, вот она в символической форме.
Опять же, столбцы — пол, строки — уровни образования. A, B, C и D — исходные данные. Таким образом, B — это женщины с учеными степенями. C — это мужчины, имеющие только высшее образование. Это сырые данные.
E и F — итоги строк. Мы добавляем через ряды, чтобы получить все правильно.
Таким образом, A плюс C равно E. B плюс D равно F. E будет общим числом людей только с высшим образованием. Так что это будут самцы и самки.
F — это общее количество людей только с ученой степенью. Опять же, это будут мужчины плюс женщины. G и H — итоги столбца. Таким образом, мы добавляем вниз, чтобы получить все внизу. A плюс B равно G. C плюс D равно H.
Итак, G — общее количество женщин, H — общее количество мужчин. В обоих этих случаях мы просто смешиваем все степени вместе. Наконец, T, нижний правый прямоугольник, представляет собой общую сумму. Это все во всей компании, все в коллекции. И мы можем получить это либо сложив в нижней строке G плюс H равно T.
Или мы можем добавить вниз правую колонку, E плюс F равно T. Итак, все должно быть проверено. Все эти суммы должны быть равны. Итак, попробуйте еще раз ответить на этот вопрос, и тогда мы решим его методом двойной матрицы. Здесь вы можете поставить видео на паузу.
Хорошо. Итак, в вопросе даны четыре числа, и я собираюсь записать их в нашу двойную матрицу.
Итак, как мы сказали выше, если есть 120 женщин, должно быть 180 мужчин, чтобы в сумме их было 300.
Точно так же, если есть 200 ученых степеней, должно быть 100 только с дипломами колледжей. Опять же, в сумме они составляют 300. Теперь посмотрите вниз на мужской ряд. У нас есть 80 плюс пробел, равно 180. Так что же должно быть в этом пробеле?
Очевидно, 100. Должно быть 100 мужчин с учеными степенями. Таким образом, 80 плюс 100 равно 180. Что ж, теперь взгляните на категорию ученых степеней. У нас есть пробел плюс 100 равно 200. Так что ясно, что это тоже должно быть 100.
Должно быть 100 женщин с учеными степенями. Это ответ, который мы ищем. Давайте просто проверим и убедимся, что это работает. Мы смотрим вниз по женскому столбцу, пустое место плюс 100 должно равняться 120, так что это будет означать, что это будет равно 20. Затем мы прибавляем к этой верхней строке 20 плюс 80 равно 100.
эта компания. Если одна из переменных имеет три категории, для этого потребуются четыре, или четыре строки, или четыре столбца.
Потому что опять же, нам понадобится по одному для каждой категории, а также один для общего количества.
Конечно, информация может быть представлена в простой числовой форме, как в предыдущей задаче, или в какой-либо другой форме, в виде отношений или в алгебраической форме. Что-то вроде того. Есть много разных способов, которыми числа могут быть даны. Вот относительно сложная проблема. Так что остановите видео, а потом мы поговорим об этом.
Хорошо. В одной школе 80 первокурсников, 100 второкурсников и 220 старшеклассников, набранных из трех городов. Все в порядке. Итак, прежде всего, 80, 100 и 220 — это суммы для разных классов.
Уровни обучения являются одной из наших категорий, поэтому у них есть одна из наших переменных, у них есть три категории. И у нас есть итоги в каждой из этих трех категорий. Тогда у нас есть три города. Это будет другая переменная. Из какого города студент?
И у нас есть три категории. И здесь нам дают информацию в процентах.
60 из, 60% из A, 30% из B, остальное из C. И затем у нас есть некоторые другие части информации. Все студенты из C — первокурсники. Половина учеников из B — старшеклассники, а остальные поровну распределены между двумя другими классами.
Сколько второкурсников из А? Так что для этого нам нужна огромная двойная матричная таблица, и здесь я написал итоги для первокурсников, второкурсников и старшеклассников. И я просто пошел вперед и просуммировал нижний ряд, чтобы получить 400. Итак, это общее количество людей в школе. Итак, теперь мы можем начать думать о процентной информации.
60% учеников из А. Нам нужно 60% от 400. Что ж, 10% от 400 равно 40. Умножьте это на шесть и получите 240. Это 60%. Тогда 30% из B.
Что ж, 30% — это только половина от 60%, значит, половина от 240 — это 120. 30 плюс 60 — это 90, значит, последние 10% взяты из C. Итак, 10% от 40, 400, конечно, это всего лишь 40. Итак, теперь у нас есть все итоги строк и столбцов. Тогда у нас есть эта большая часть информации.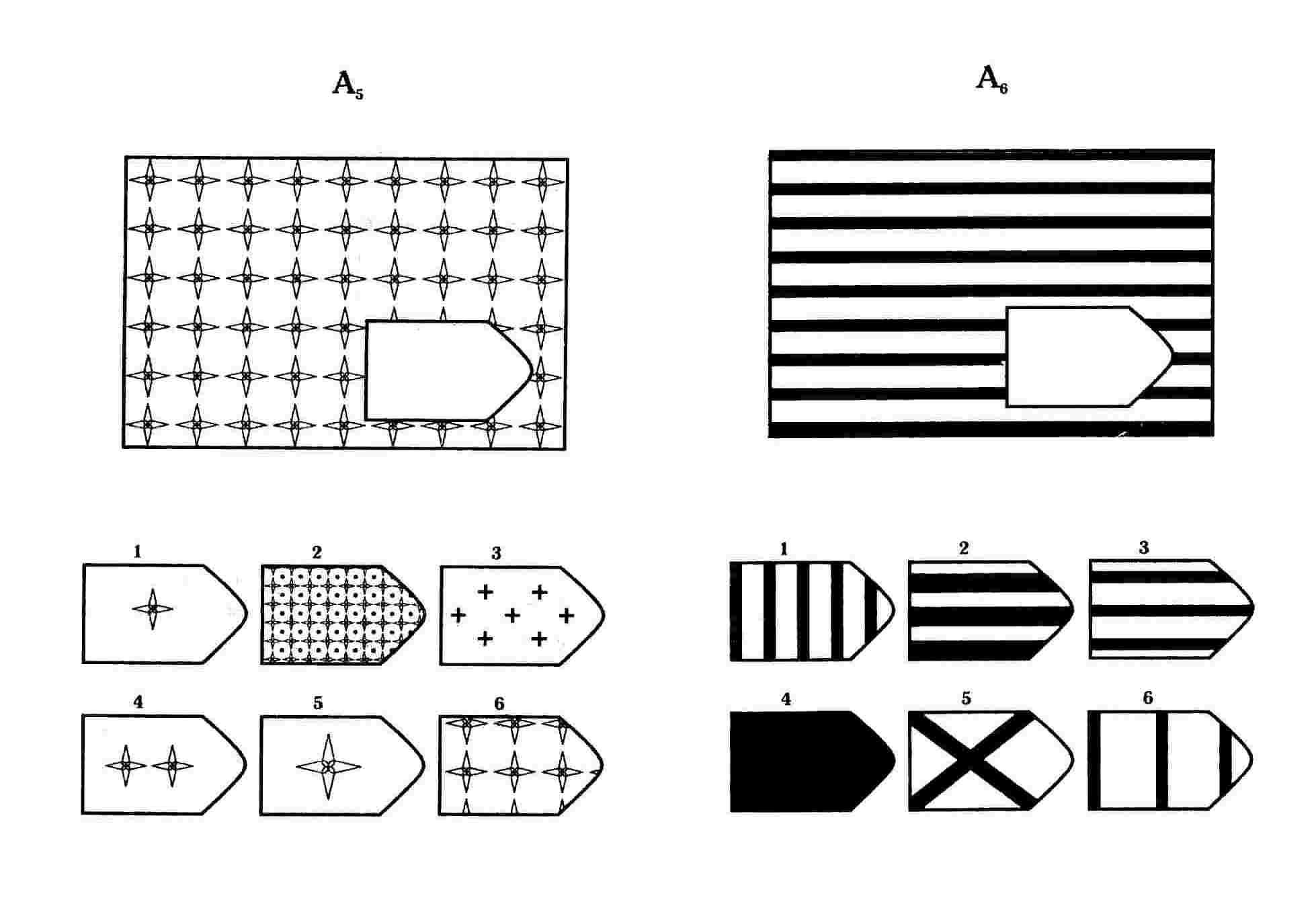
Все студенты из C — первокурсники.
Итак, 40 студентов из C. Все 40 первокурсников. И тогда мы можем просто поставить нули в эти столбцы. Так что это чрезвычайно упрощает все. Теперь нам говорят, что половина учеников из Б — старшеклассники. Таким образом, половина от 120 равна 60.
Половина из них старшеклассники. А остальные 60 поделены поровну, так что 30 и 30. Итак, теперь нам нужны второкурсники из А. Мы посмотрим на колонку второкурсников. У нас есть пробел плюс 30 плюс 0 равно 100. Ясно, что это число должно быть 70, и это наш ответ.
Метод двойной матрицы может значительно упростить задачи, в которых каждый элемент помещается в две разные категории. Записи в строке суммируются с суммами строк в крайнем правом столбце. Записи в столбцах суммируются с итоговыми значениями столбца в нижней строке. И общая сумма в нижнем правом поле — это все.
Это равно сумме сумм строк, а также сумме сумм столбцов.
Как, черт возьми, инвертировать матрицу? И почему?
Предупреждение и задача со словом
Purplemath
Можно ли разделить на матрицу?
Для матриц нет такого понятия, как деление.
Вы можете складывать, вычитать и умножать матрицы, но не можете их делить. Однако существует родственная концепция, которая называется «инверсия». Сначала я объясню, почему инверсия полезна, а затем покажу вам, как это сделать.
Содержание продолжается ниже
MathHelp.com
Вспомните, когда вы впервые узнали о том, как решать линейные уравнения. Если бы вам дали что-то вроде 3 x = 6, вы бы решили, разделив обе части на 3. Поскольку умножение на 1/3 равносильно делению на 3, вы также можете умножить обе части на 1/3, чтобы получить тот же ответ: x = 2.
Если вам нужно решить что-то вроде (3/2) x = 6, вы все равно можете разделить обе части на 3/2, но, вероятно, было проще умножить обе стороны на 2/3. Обратная дробь 2/3 обратна 3/2, потому что, если вы перемножите две дроби, вы получите 1, что в данном контексте называется (мультипликативной) тождественностью;: 1 называется мультипликативной тождественностью, потому что умножение чего-либо на 1 не меняет своего значения.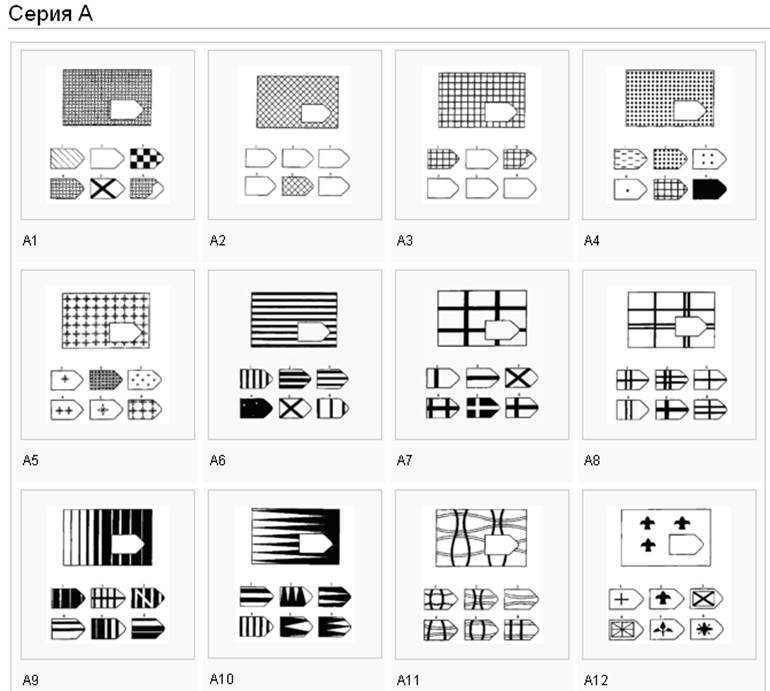
Эта терминология и эти факты очень важны для матриц. Если вам дано матричное уравнение типа AX = C , где вам даны A и C и вам предлагается вычислить X , вы хотели бы разделить матрицу A . Но вы не можете делать деление с матрицами.
Для чего используются обратные матрицы?
Учитывая матричное уравнение AX = C , что, если бы вы могли найти обратную
АХ = С
А −1 АХ = А −1 С
IX = А −1 С
X = A −1 C
Как « A −1 AX » в левой части уравнения (во второй строке выше) превратилось в «
Вспомните природу инверсий для правильных чисел.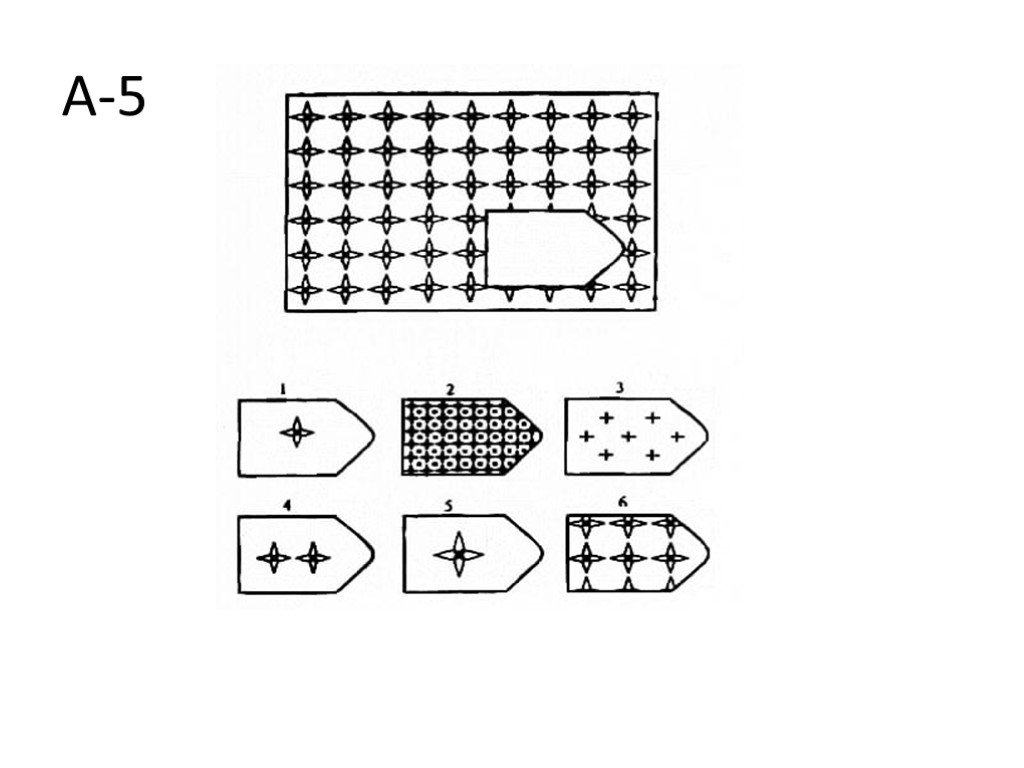
Если у вас есть число (например, 3/2) и обратное ему число (в данном случае 2/3), и вы умножаете их, вы получаете 1. А 1 — это мультипликативное тождество, называемое так потому, что 1 x = x для любого числа x .
Инверсия работает так же для матриц. Если вы умножите матрицу (такую как A ) и ее обратную (в данном случае A −1 ), вы получите единичную матрицу I , которая является матричным аналогом числа 1. И точка единичной матрицы состоит в том, что
Следует отметить, что порядок умножения выше важен и вовсе не произволен. Напомним, что для матриц умножение не является коммутативным. то есть AB почти никогда не совпадает с BA .
Таким образом, умножение матричного уравнения «слева» (чтобы получить A −1 AX ) совсем не то же самое, что умножение «справа» (чтобы получить AXA −1 ).
Вместо этого вы должны умножить A −1 слева, поместив его рядом с A в исходном матричном уравнении. А поскольку при решении вы должны проделать одно и то же с обеими частями уравнения, вы должны умножить «слева» и на правую часть уравнения, в результате чего получится A — 1 С .
Нельзя быть небрежным в размещении матриц; вы должны быть точными, правильными и последовательными. Это единственный способ успешно отменить
Как вы видели выше, обратные матрицы могут быть очень полезны для решения матричных уравнений. Но…
Как найти обратную матрицу?
Чтобы найти обратную матрицу, выполните следующие действия:
- Запишите матрицу, которую вы хотите инвертировать.
- Добавьте к этой матрице единичную матрицу, сделав одну матрицу, которая теперь в два раза шире, чем в высоту.
- Используя операции со строками, преобразуйте левую половину двойной ширины в единичную матрицу.
- Новая правая часть двойной ширины является обратной исходной матрице.
Этот метод инвертирования матриц довольно умный. Вот пример того, как это работает:
- Найдите обратное число .
Сначала я записываю элементы матрицы A , но я записываю их в матрицу двойной ширины:
В другой половине матрицы двойной ширины я записываю единичную матрицу:
Теперь я буду выполнять операции со строками матрицы, чтобы преобразовать левая сторона двойной ширины в личность. (Как всегда с операциями со строками, не существует единственного «правильного» способа сделать это. Ниже приведены лишь шаги, которые произошли со мной. Ваши расчеты легко могут выглядеть совершенно по-другому.)
Теперь, когда левая часть двойной ширины содержит единицу, правая часть содержит обратную.
То есть обратная матрица следующая:
Откуда вы знаете, что эта матрица является обратной?
Обратите внимание, что мы можем подтвердить, что эта матрица является обратной A , перемножив две матрицы и увидев, что мы получаем тождество.
Поскольку умножение закончилось единичной матрицей, подтверждено, что найденная нами матрица является обратной исходной матрице, которую нам дали.
Имейте в виду, что в «реальной жизни» обратная матрица редко представляет собой матрицу, заполненную красивыми аккуратными целыми числами, подобными этому. Однако, если повезет, особенно если вы делаете инверсии вручную, вам дадут хорошие, подобные этому.
Есть ли формула для инвертирования матрицы 2×2?
Чтобы найти обратную матрицу 2 на 2, используйте следующую формулу:
Для следующей матрицы:
…обратная матрица определяется как:
Существует ли формула для обращения матрицы 3×3 ?
Существует своего рода формула для обратной матрицы 3 на 3, но это, возможно, не самый быстрый способ.
