Пошаговый Калькулятор Линейной Регрессии — Mathcracker.Com
Инструкции: Проведите регрессионный анализ с помощью Калькулятор Линейной Регрессии где будет найдено уравнение регрессии и предоставлен подробный отчет о расчетах, а также диаграмма рассеяния. Все, что вам нужно сделать, это ввести данные X и Y. По желанию можно добавить заголовок и название переменных.
Подробнее об этом калькуляторе линейной регрессии
A
модель линейной регрессии
соответствует линейной модели, которая минимизирует сумму квадратов ошибок для набора пар \((X_i, Y_i)\).
Это означает, что вы предполагаете существование модели, которая в упрощенной форме имеет вид \(Y = \alpha + \beta X\), а затем вы отмечаете несоответствия (ошибки), обнаруженные при использовании этой линейной модели для прогнозирования набора заданных данных.
Для каждого \(X_i\) в данных вы вычисляете \(\hat Y_i = \alpha + \beta X_i\) и вычисляете ошибку, измеряя \(Y_i — \hat Y_i\). В частности, в этом случае вы берете квадрат каждого несоответствия/ошибки и суммируете ВСЕ эти квадраты ошибок.
Задача регрессионного калькулятора — найти наилучшие значения \(\alpha\) и \(\beta\), чтобы сумма квадратов ошибок была как можно меньше.
Формула регрессии
Уравнение линейной регрессии, также известное как уравнение наименьших квадратов, имеет следующую форму: \(\hat Y = a + b X\), где коэффициенты регрессии представляют собой значения \(a\) и \(b\).
Вопрос в том: Как рассчитать коэффициенты регрессии? Коэффициенты регрессии вычисляются этим регрессионным калькулятором следующим образом:
\[b = \frac{SS_{XY}}{SS_{XX}}\] \[a = \bar Y — \bar X \cdot b \]
Это формулы, которые вы использовали, если бы вычисляли уравнение регрессии вручную, но, вероятно, вы предпочтете использовать калькулятор (наш
Калькулятор регрессии
), который покажет вам важные шаги.
Эта формула линейной регрессии интерпретируется следующим образом: коэффициент \(b\) известен как коэффициент наклона, а коэффициент \(a\) известен как точка пересечения по оси y.
Если вместо линейной модели вы хотите использовать нелинейную модель, то вам следует рассмотреть вместо нее модель калькулятор полиномиальной регрессии , что позволяет использовать мощности независимой переменной.
Калькулятор линейной регрессии шаги
Прежде всего, вы хотите оценить, имеет ли смысл проводить регрессионный анализ. Итак, сначала вы должны запустить это
калькулятор коэффициента корреляции
чтобы увидеть, существует ли значительная степень линейной связи между переменными.
Итак, сначала вы должны запустить это
калькулятор коэффициента корреляции
чтобы увидеть, существует ли значительная степень линейной связи между переменными.
Другими словами, имеет смысл проводить регрессионный анализ только в том случае, если коэффициент корреляции достаточно силен, чтобы обосновать модель линейной регрессии. Кроме того, вы должны использовать это калькулятор точечной диаграммы чтобы убедиться, что визуальный рисунок действительно линейный.
Можно предположить, что коэффициент корреляции близок к 1, но тем не менее характер связи вовсе не линейный.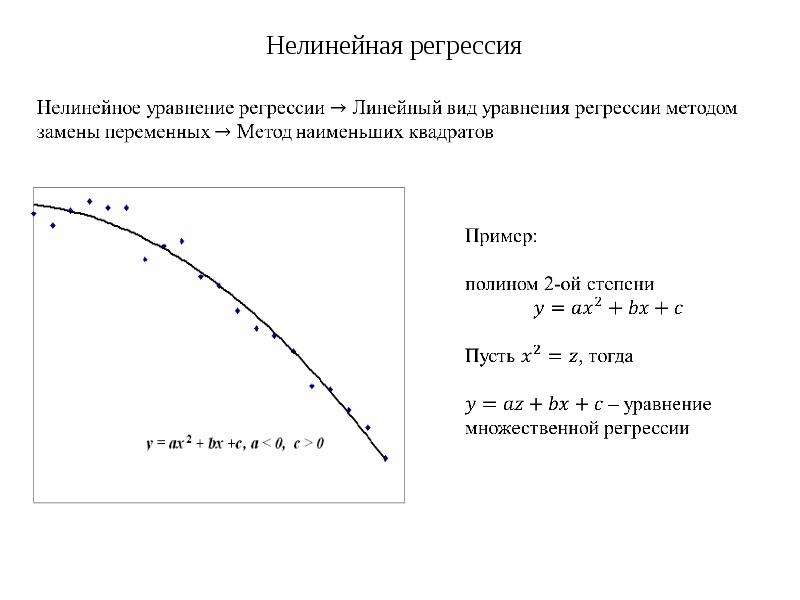
Шаги для проведения регрессионного анализа следующие:
Шаг 1: Получите данные для зависимой и независимой переменной в формате столбца.
Шаг 2:
Шаг 3:
Нажмите «Рассчитать».
Этот калькулятор уравнения регрессии с шагами предоставит вам все необходимые расчеты в организованном порядке, чтобы вы могли четко понять все этапы процесса.
Остатки регрессии
Как оценить, хороша ли модель линейной регрессии? Вы можете подумать: «Легко, просто посмотрите на scatterplot «. В действительности математика и статистика обычно выходят за пределы того, где глаз встречается с графиком. Обычно рискованно полагаться только на диаграмму рассеяния для оценки качества модели.
С точки зрения хорошего соответствия, один из способов оценки качества соответствия модели линейной регрессии заключается в следующем
вычисление коэффициента детерминации
показывает долю вариации зависимой переменной, которая объясняется независимой переменной.
В линейной регрессии выполнение предположений имеет решающее значение для того, чтобы оценки коэффициента регрессии обладали хорошими свойствами (несмещенность, минимальная дисперсия и др.).
Для того чтобы оценить предположения линейной регрессии, необходимо посмотреть на остатки. Для этого вы можете взглянуть на нашу программу калькулятор остатков .
Предсказательная сила уравнения регрессии
Как узнать, правильно ли найдено уравнение регрессии? Или лучше вопрос, как узнать, имеет ли оцениваемое уравнение регрессии хорошую предсказательную силу?
Что вам нужно сделать, это
вычислить коэффициент детерминации
, который сообщает вам величину вариации зависимой переменной, которая объясняется зависимой(ыми) переменной(ями). 2 = 0.64\), и интерпретация состоит в том, что 64% вариации зависимой переменной объясняются независимой переменной в этой модели.
2 = 0.64\), и интерпретация состоит в том, что 64% вариации зависимой переменной объясняются независимой переменной в этой модели.
Полиномиальная регрессия
Как мы упоминали ранее, бывают случаи, когда линейная регрессия просто не подходит, потому что существует четкая нелинейная модель, определяющая взаимосвязь между двумя переменными.
Ваш первый сигнал о том, что вместо линейной регрессии следует использовать полиномиальную регрессию, заключается в том, что вы видите, что в данных, представленных диаграммой рассеяния, присутствует криволинейный паттерн.
Если это так, вы можете попробовать это
калькулятор полиномиальной регрессии
, чтобы оценить нелинейную модель, которая имеет больше шансов на лучшее соответствие.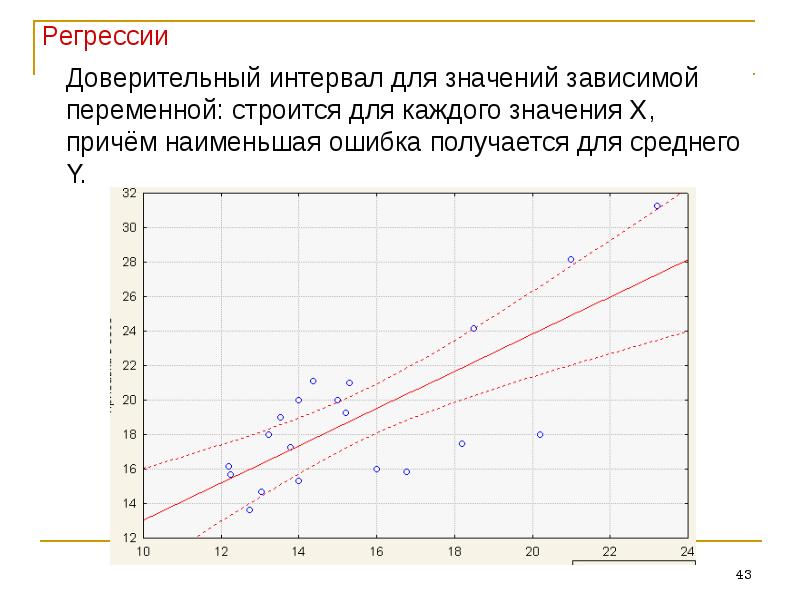
Что дает этот онлайн-калькулятор линейной регрессии?
Сначала вы получаете таблицу данных и вычисляете соответствующие квадраты и перекрестные умножения, чтобы получить требуемую сумму квадратов значений, необходимую для применения формулы регрессии.
Как только все это будет аккуратно отображено в таблице со всеми необходимыми столбцами, будут показаны формулы регрессии с подставленными правильными значениями, а затем с выводом о модели линейной регрессии, которая была оценена на основе данных.
Кроме того, строится точечная диаграмма, чтобы оценить, насколько тесна линейная связь между переменными, что дает представление о том, насколько хороша модель линейной регрессии.
Является ли r2 коэффициентом регрессии?
Нет. Технически коэффициенты регрессии — это оценочные коэффициенты, являющиеся частью регрессионной модели. Коэффициент r2 называется коэффициентом детерминации.
Коэффициент r2 также рассчитывается по выборочным данным, но это не коэффициент регрессии, но это не значит, что он не важен. Коэффициент r2 важен, потому что он дает оценку процента вариации, объясняемой моделью.
Как сделать линейную регрессию в excel?
В Excel есть возможность проводить линейную регрессию либо непосредственно с помощью команд «=НАКЛОН()» и «=ИНТЕРЦЕПТ()», либо с помощью меню «Анализ данных».
Но Excel не показывает все шаги, как это делает наш регрессионный калькулятор.
Другие калькуляторы, связанные с линейной регрессией
Этот
Калькулятор уравнения регрессии
является лишь одним из многих калькуляторов, представляющих интерес при работе с линейными моделями. Вас также могут заинтересовать
вычисление коэффициента корреляции
, или в
построить диаграмму рассеяния
с предоставленными данными. 2 = 0,67 при оценке линейной регрессии Y как функции X, тогда интерпретация заключается в том, что X объясняет 67% вариации Y.
2 = 0,67 при оценке линейной регрессии Y как функции X, тогда интерпретация заключается в том, что X объясняет 67% вариации Y.
Что происходит, когда у вас больше переменных
Потенциально у вас может быть более одной независимой переменной. Например, вы можете быть заинтересованы в оценке Y в терминах двух переменных X1 и X2. В этом случае вам необходимо рассчитать множественную линейную регрессию модель, где идея по сути та же: найти гиперплоскость, которая минимизирует сумму квадратов ошибок.
Онлайн калькулятор: Аппроксимация функции одной переменной
Данный калькулятор по введенным данным строит несколько моделей регрессии: линейную, квадратичную, кубическую, степенную, логарифмическую, гиперболическую, показательную, экспоненциальную. Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.
Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.
Если не ввести значения x, калькулятор примет, что значение x меняется от 0 с шагом 1.
Аппроксимация функции одной переменной
83 71 64 69 69 64 68 59 81 91 57 65 58 62Значения x, через пробел
183 168 171 178 176 172 165 158 183 182 163 175 164 175Значения y, через пробел
Линейная аппроксимация Квадратичная аппроксимация Кубическая аппроксимация Аппроксимация степенной функцией Показательная аппроксимация Логарифмическая аппроксимация Гиперболическая аппроксимация Экспоненциальная аппроксимацияТочность вычисленияЗнаков после запятой: 4
Линейная регрессия
Коэффициент линейной парной корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Квадратичная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Кубическая регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Степенная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Показательная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Логарифмическая регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Гиперболическая регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Экспоненциальная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Результат
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Сначала сформулируем задачу:
Пусть у нас есть неизвестная функция y=f(x), заданная табличными значениями (например, полученными в результате опытных измерений).
Нам необходимо найти функцию заданного вида (линейную, квадратичную и т. п.) y=F(x), которая в соответствующих точках принимает значения, как можно более близкие к табличным.
На практике вид функции чаще всего определяют путем сравнения расположения точек с графиками известных функций.
Полученная формула y=F(x), которую называют эмпирической формулой, или уравнением регрессии y на x, или приближающей (аппроксимирующей) функцией, позволяет находить значения f(x) для нетабличных значений x, сглаживая результаты измерений величины y.
Для того, чтобы получить параметры функции F, используется метод наименьших квадратов. В этом методе в качестве критерия близости приближающей функции к совокупности точек используется суммы квадратов разностей значений табличных значений y и теоретических, рассчитанных по уравнению регрессии.
Таким образом, нам требуется найти функцию F, такую, чтобы сумма квадратов S была наименьшей:
Рассмотрим решение этой задачи на примере получения линейной регрессии F=ax+b.
S является функцией двух переменных, a и b. Чтобы найти ее минимум, используем условие экстремума, а именно, равенства нулю частных производных.
Используя формулу производной сложной функции, получим следующую систему уравнений:
Откуда, выразив a и b, можно получить формулы для коэффициентов линейной регрессии, приведенные выше.
Аналогичным образом выводятся формулы для остальных видов регрессий.
Калькулятор линейной регрессии
Интерпретация результатов
Используя формулу Y = m X + b :
- Линейная регрессионная интерпретация коэффициента уклона, м , такова: «Расчетное изменение Y при увеличении X на 1 единицу».
- Интерпретация параметра перехвата b такова: «Оценочное значение Y, когда X равно 0».
Первая часть результатов содержит наиболее подходящие значения наклона и Y-пересечения. Эти оценки параметров строят линию регрессии наилучшего соответствия. Вы можете увидеть, как они вписываются в уравнение в нижней части раздела результатов. Наше руководство поможет вам узнать больше об интерпретации наклонов регрессии, точек пересечения и доверительных интервалов.
Наше руководство поможет вам узнать больше об интерпретации наклонов регрессии, точек пересечения и доверительных интервалов.
Используйте раздел качества подгонки, чтобы узнать, насколько близки отношения. R-квадрат количественно определяет процент изменения Y, который можно объяснить его значением X.
Следующий вопрос может показаться странным на первый взгляд: является ли наклон существенно отличным от нуля? Это восходит к параметру наклона, в частности. Если он значительно отличается от нуля, то есть основания полагать, что X можно использовать для предсказания Y. Если нет, то линия модели ничем не лучше, чем отсутствие линии вообще, поэтому модель не особенно полезна!
P-значения помогают в интерпретации здесь: если оно меньше некоторого порога (часто 0,05), у нас есть данные, позволяющие предположить статистически значимую связь.
Наконец, уравнение приведено в конце раздела результатов. Подставьте любое значение X (в любом случае в пределах диапазона набора данных), чтобы вычислить соответствующий прогноз для его значения Y.
График линейной регрессии
Калькулятор линейной регрессии предоставляет общий график ваших данных и линию регрессии.
Хотя график на этой странице нельзя настраивать, Prism — это полнофункциональный исследовательский инструмент, используемый для визуализации данных с качеством публикации. Посмотрите это в действии в нашем видеоролике «Как создавать и настраивать высококачественные графики»!
Графики важны не только для визуализации, но и для проверки наличия выбросов в ваших данных. Если есть пара точек, далеких от всех остальных, есть несколько возможных значений: они могут чрезмерно влиять на ваше уравнение регрессии, или выбросы могут быть очень важным открытием сами по себе. Используйте этот контрольный список выбросов, чтобы выяснить, что более вероятно в вашем случае.
Для дополнительной информации
Понравилось использовать этот калькулятор? Для дополнительных функций, таких как расширенный анализ и настраиваемая графика, мы предлагаем бесплатную 30-дневную пробную версию Prism.
Некоторые дополнительные возможности Prism включают в себя возможность:
- Используйте уравнение наилучшего соответствия для прогнозирования непосредственно в программном обеспечении.
- Графические доверительные интервалы и использование расширенных интервалов прогнозирования
- Сравните кривые регрессии для разных наборов данных
- Создайте несколько моделей регрессии (используйте более одной переменной-предиктора)
Хотите узнать больше о линейном регрессионном анализе? Наше окончательное руководство по линейной регрессии включает примеры, ссылки и интуитивно понятные объяснения по этому вопросу.
Руководство Prism по подбору кривых также включает подробные ресурсы по линейной регрессии в полезном формате часто задаваемых вопросов.
Оба этих ресурса также проводят множественный линейный регрессионный анализ, аналогичный метод, используемый для большего количества переменных. Если в оценке отклика задействовано более одного предиктора, следует попробовать множественный линейный анализ в Prism (а не в калькуляторе на этой странице!).
Хотите увидеть, как выглядит регрессионный анализ от начала до конца?
Посмотрите наше видео ниже о том, как выполнить линейную регрессию в Prism.
Мы рекомендуем:
Аппроксимация функции с помощью регрессионного анализа
Проблема аппроксимации функции заключается в том, как выбрать функцию из четко определенного класса, которая точно соответствует («аппроксимирует») целевой неизвестной функции.
Этот калькулятор использует предоставленные данные таблицы целевых функций в виде точек {x, f(x)} для построения нескольких моделей регрессии, а именно: линейной регрессии, квадратичной регрессии, кубической регрессии, степенной регрессии, логарифмической регрессии, гиперболической регрессии, ab -экспоненциальная регрессия и экспоненциальная регрессия. Результаты можно сравнивать по коэффициенту корреляции, коэффициенту детерминации, средней относительной ошибке (стандартной ошибке регрессии) и визуально, на графике. Теория и формулы, как обычно, даны под калькулятором.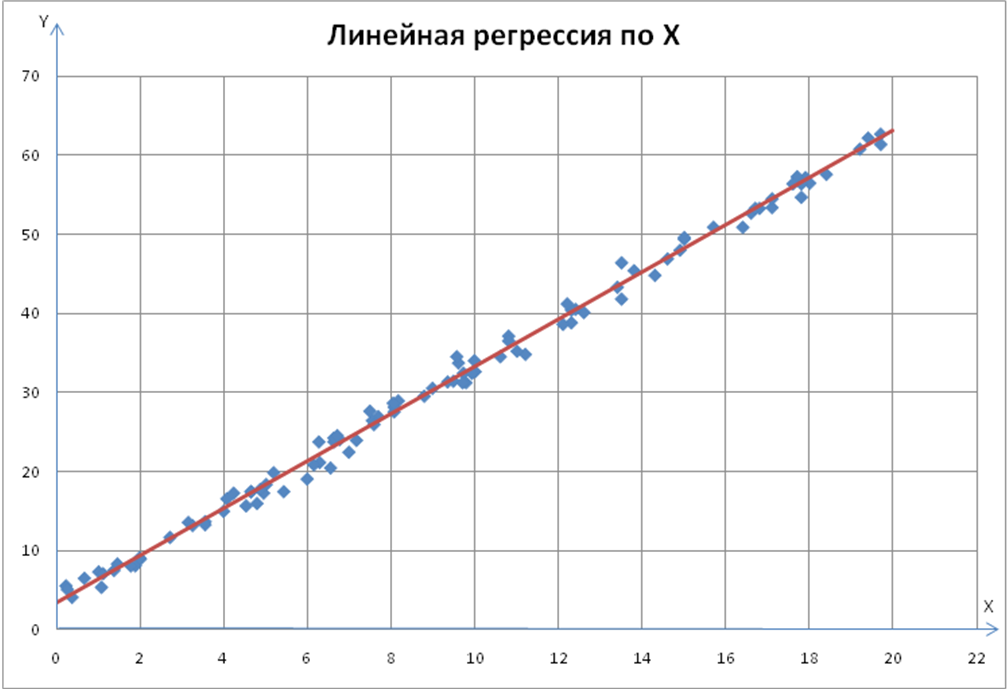
Аппроксимация функции с помощью регрессионного анализа
83 71 64 69 69 64 68 59 81 91 57 65 58 62Значения X, разделенные пробелом
183 168 171 17 8 176 172 165 158 183 182 163 175 164 175Значения Y, разделенные пробелом
Линейная регрессия Квадратичная регрессия Кубическая регрессия Степенная регрессия ab-Экспоненциальная регрессия Логарифмическая регрессия Hyperbo личная регрессия Экспоненциальная регрессия Точность вычисленийЗнаки после запятой: 4
Линейная регрессия
Коэффициент линейной корреляции
Коэффициент детерминации
Средняя относительная ошибка, %
Квадратичная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя относительная ошибка, %
Кубическая регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя относительная ошибка, %
Регрессия мощности
Коэффициент корреляции
Коэффициент детерминации
Средняя относительная ошибка, %
ab-Экспоненциальная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя относительная ошибка, %
Логарифмическая регрессия
Корреляция коэффициент
Коэффициент детерминации
Средняя относительная ошибка, %
Гиперболическая регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя относительная ошибка, %
Экспоненциальная регрессия
Коэффициент корреляции
Коэффициент детерминации
9000 9
Средняя относительная ошибка, %
Результаты
Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.
Во время загрузки и создания может происходить замедление работы браузера.
Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – те же формулы, что и в случае квадратичной регрессии.
Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – те же формулы, что и выше.
Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – то же.
Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии — те же, что и выше.
Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – те же, что и выше.
Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – те же, что и выше.
Начнем с задачи:
Имеем неизвестную функцию y=f(x), заданную в виде табличных данных (например, таких, как полученные из экспериментов).
Требуется найти функцию с известным типом (линейная, квадратичная и т.д.) y=F(x), значения которых должны быть максимально приближены к табличным значениям в тех же точках. На практике тип функции определяют путем визуального сравнения точек таблицы с графиками известных функций.
На практике тип функции определяют путем визуального сравнения точек таблицы с графиками известных функций.
В результате мы должны получить формулу y=F(x), называемую эмпирической формулой (уравнение регрессии, функция аппроксимации), которая позволяет вычислить y для x, не представленных в таблице. Таким образом, эмпирическая формула «сглаживает» значения y.
Мы используем метод наименьших квадратов , чтобы получить параметры F для наилучшего соответствия. Наилучшее соответствие по методу наименьших квадратов минимизирует сумму квадратов невязок, причем невязка представляет собой разницу между наблюдаемым значением и подобранным значением, предоставленным моделью.
Таким образом, когда нам нужно найти функцию F, такую как сумма квадратов невязок, S будет минимальным
Опишем решение этой задачи на примере линейной регрессии F=ax+b.
Нам нужно найти наилучшее соответствие для коэффициентов a и b, таким образом, S является функцией a и b.
