Квадрат Декарта для принятия решений
Жизнь человека состоит из череды принятых им решений и их последствий. Когда мы сталкиваемся с трудностями, то задействуем свой опыт, а иногда перекладываем ответственность выбора на окружающих, и нередко делаем это с оглядкой на ожидания социума. Однако на самом деле наш лучший помощник в принятии решений – собственный разум. В особо стрессовых ситуациях не помешала бы формула, с помощью которой мы могли бы легко взвесить все плюсы и минусы рассматриваемого вопроса. И этой формулой может стать Квадрат Декарта – действенная техника, позволяющая получить наиболее эффективный результат и не ошибиться в выборе.
Что такое Квадрат Декарта и в чем его преимущества
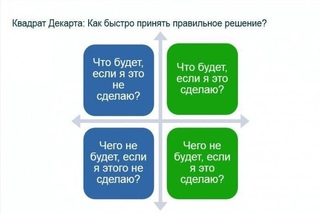
В основе техники, разработанной известным французским математиком, инженером и философом Рене Декартом, лежат четыре вопроса:
- Что я получу, если это произойдет?
- Что я получу, если этого не произойдет?
- Что я потеряю, если это произойдет?
- Что я потеряю, если этого не произойдет?
Честные и вдумчивые ответы позволят вам рассмотреть вопрос со всех сторон и прийти к нужному решению.
Чем этот способ отличается от классических двух столбиков с аргументами за и против? Традиционный метод, без сомнения, работает, но часто мы не можем ограничиться только плюсами и минусами, потому что нам требуется больше вариантов и проблема должна быть рассмотрена с разных углов. Кроме того, обычно мы задаем себе только один вопрос: «Что случится, если это произойдет?». Из-за такого упрощения, сами того не понимая, мы загоняем себя в ловушку и не пропускаем целый пласт других критериев
Увидеть ситуацию с разных точек зрения позволяет Квадрат решений Декарта. Благодаря ему вы не будете однобоко фокусироваться на положительной и отрицательной сторонах вопроса, а проанализируете все необходимые аспекты. Среди других важных преимуществ техники – она проста, универсальна и применима при решении вопросов любой важности: как глобальных, так и бытовых; как в работе, так и в личной жизни.
Квадрат Декарта для принятия решений – инструмент, который позволяет семь раз отмерить, прежде чем отрезать
Как использовать Квадрат Декарта на практике?
Для начала вооружитесь карандашом или ручкой и подготовьте лист бумаги.
Разберем, как использовать методику, на конкретном примере. Допустим, вы размышляете, стоит ли переехать жить в другую страну. Конечно, можно просто задать себе тот самый заветный вопрос: «Что случится, если я перееду?». Это позволит сразу оценить все преимущества, но таким образом вам не удастся прийти к пониманию полноценного, всеобъемлющего ответа, потому что ситуация не будет рассмотрена со всех сторон.
При помощи данной техники принятия решений вы сможете взглянуть на проблемную ситуацию
Вопрос 1. Что я получу, если это произойдет?
Ответив на этот вопрос, вы выявите список преимуществ – в данном случае плюсов смены места жительства. Ваша мотивация напрямую зависит от того, что вы напишете в этом столбце, поэтому постарайтесь придумать как можно больше положительных моментов и ни в коем случае не останавливаться на первом, что пришло вам на ум.
Ваша мотивация напрямую зависит от того, что вы напишете в этом столбце, поэтому постарайтесь придумать как можно больше положительных моментов и ни в коем случае не останавливаться на первом, что пришло вам на ум.
- Если я это сделаю
- Если я это сделаю, это вдохнет свежего воздуха в мою жизнь, нивелирует рутину.
- Если я это сделаю, мне больше не придется общаться с надоедливыми нетактичными родственниками и приглашать их в гости.
- Если я это сделаю, то буду больше уважать себя и моя самооценка повысится, ведь для такого поступка нужна смелость.
- Если я это сделаю, то у меня появится мотивация наконец-то выучить иностранный язык и завести новые интересные знакомства.
- Если я это сделаю, то смогу доказать окружающим меня людям, что я способен добиться успеха и в корне изменить свою жизнь.

Вопрос 2. Что я получу, если этого не произойдет?
Этот вопрос связан с поиском плюсов в случае отказа от перемен. Представьте ситуацию, в которой все остается в текущем состоянии. Подумайте о тех положительных моментах, которыми вы обладаете здесь и сейчас и которые вы не хотите потерять.
- Если я этого не сделаю, мне не придется объясняться перед начальником, коллегами, друзьями и родственниками по поводу моего отъезда.
- Если я этого не сделаю сейчас, я всегда могу переехать через год-другой, подкопив перед этим денег и обеспечив себе более комфортные условия. Возможно сейчас не лучшее время для такой авантюры.
- Если я этого не сделаю, мне не придется много заниматься на языковых курсах и стараться адаптироваться к чужой культуре, потому что в этом не будет нужды.
- Если я этого не сделаю, то смогу спокойно уделять время отдыху и семье, в то время как хлопоты, связанные с переездом, нарушат традиционный уклад моей жизни и неизбежно приведут к стрессу.

- Если я этого не сделаю, то моя мечта об идеальном месте жительства останется со мной и я смогу черпать из нее энергию и вдохновение.
- Если я не перееду, то у меня и дальше будет большой оплачиваемый отпуск, в то время как за границей он значительно короче.
Вопрос 3. Что я потеряю, если это произойдет?
Этот пункт обозначит минусы положительного решения. Подумайте, чего вам будет не хватать – возможно, сейчас вы упускаете из вида очевидные преимущества, которыми обладаете.
- Если я сделаю это, придется на корню менять устоявшиеся привычки и образ жизни: самому считать налоги; экономить на воде и электричестве; осваивать раздельный сбор мусора и пр.
- Если я сделаю это, придется усиленно работать, и мне будет не хватать времени на привычные развлечения.
- Если я это сделаю, то не смогу встречаться с друзьями в выходные и отметить с ними Новый год с оливье под бой курантов.
- Если я перееду, некому будет заботиться о моих родителях: помогать им с дачей, тяжелыми сумками и ремонтом.

- Если я сделаю это, придется потратиться на чипирование, прививки, перевозку домашнего животного, а также выплачивать дорогую страховку за его содержание.
- Если я это сделаю, окружающие люди могут счесть меня непатриотичным.
Вопрос 4. Что я потеряю, если этого не произойдет?
Этот вопрос поможет вам выделить определенные недостатки решения в пользу изменений. В то же время записанными здесь пунктами вы отсекаете различные «не», связанные с отказом от выполнения действия. Отвечать необходимо быстро и интуитивно.
- Если я не сменю страну проживания, я не воплощу в реальность свою мечту, и это будет меня тяготить.
- Если я не перееду, до конца жизни буду задаваться вопросом: «А что было бы, если бы…?»
- Если я этого не сделаю, то буду считать себя трусом и неудачником.
- Если я не перееду, то не приобрету необходимую мотивацию для изучения иностранного языка и знакомств с новыми людьми с другим менталитетом.
- Если я не сменю страну, то не смогу доказать окружающим, что способен изменить свой образ жизни.
- Если я не перееду, то рискую надолго погрязнуть в рутине.
Нюансы и советы по использованию
Если вы решили прибегнуть к методике «Квадрат Декарта», обратите внимание на несколько важных пунктов:
- Обязательно используйте бумагу и ручку! Проговаривание вопросов в уме не будет таким эффективным – скорее всего, вы забудете часть ответов, не получите наглядную, всеобъемлющую картинку и, как следствие, не получите и нужных результатов. Кроме того, наше подсознание частенько игнорирует частицу «не», что также приводит к ошибкам.
- Постарайтесь быть максимально честным самим с собой. Берите в расчет то, что действительно важно для вас, без оглядки на мнение окружающих и социума.
- Методика Декарта хороша тем, что ее можно применять в любой неоднозначной ситуации. Чем чаще вы используете Квадрат, тем проще вам будет находить решение. Если освоить эту технику и сделать ее своей привычкой, вы научитесь продумывать собственные действия на несколько шагов вперед.
Есть простой способ убедиться в том, что вашему мозгу сложно воспринимать частицу «не». Попробуйте нарисовать заповедь «Не убий».
 Наше сознание действует по схожему принципу: оно визуализирует действие, о котором вы думаете, даже если вы используете отрицательную частицу. В итоге у вас в голове оседает мысль о самом поступке, а не о том, что он запрещен.
Наше сознание действует по схожему принципу: оно визуализирует действие, о котором вы думаете, даже если вы используете отрицательную частицу. В итоге у вас в голове оседает мысль о самом поступке, а не о том, что он запрещен.Все мы порой сталкиваемся со сложными задачами, кажущимися невыполнимыми. Важно научиться не убегать от них, а встречать с поднятой головой – для этого нужно просто найти ключ, который откроет дверь к решению, а подобрать этот ключ поможет Квадрат Декарта. Не требующая много времени и усилий, данная методика прекрасно адаптируема под любые ситуации и позволяет осветить проблему со всех сторон. Но самое, вероятно, главное ее достоинство – в том, что она привносит упорядоченность в хаос безумного темпа жизни, ведь, как говорил сам Рене Декарт, «порядок освобождает мысль».
Важно научиться не убегать от них, а встречать с поднятой головой – для этого нужно просто найти ключ, который откроет дверь к решению, а подобрать этот ключ поможет Квадрат Декарта. Не требующая много времени и усилий, данная методика прекрасно адаптируема под любые ситуации и позволяет осветить проблему со всех сторон. Но самое, вероятно, главное ее достоинство – в том, что она привносит упорядоченность в хаос безумного темпа жизни, ведь, как говорил сам Рене Декарт, «порядок освобождает мысль».
Картезианское сомнение Декарта: отражение идей философа в фильме «Матрица»: rabota_psy — LiveJournal
Люди погружены в желеобразную субстанцию. Их жизнь поддерживается многочисленными трубками и проводами, которые влияют на мозг, создавая иллюзию полноценной жизни. Это фрагмент фильма «Матрица», изображающий 2197 год. Человечество попало под власть машин. Тепло и электрическая активность человеческих тел используются искусственным интеллектом как источник энергии.Планета окутана мраком, города разрушены. Люди, порабощенные машинами, не знают об этом. Они живут в мире иллюзий, им кажется, что жизнь течет как обычно. Нео — один из них. Благодаря красной капсуле он узнает правду и начинает борьбу с суперкомпьютером.
Люди, порабощенные машинами, не знают об этом. Они живут в мире иллюзий, им кажется, что жизнь течет как обычно. Нео — один из них. Благодаря красной капсуле он узнает правду и начинает борьбу с суперкомпьютером.
Портрет Декарта кисти Франса Халса (1648)
Могла ли такая ситуация возникнуть на самом деле? Об этом еще в XVII веке задумался математик и философ Рене Декарт.
Картезианское сомненье
Возможно запереть человека в рамках сна, содержание которого определяется кем-то, создать условия, в которых индивид не будет осознавать, что воспринимаемая им реальность совсем не реальна. Чтобы поверить в это, нужно обладать скептицизмом. Именно это качество было присуще Декарту.
Диспут Декарта (справа) и королевы Кристины, картина Пьера-Луи Дюмениля
Скептиком называют человека, сомневающегося во всем. Рене Декарт — король скептиков. Ученый разработал форму скептицизма, названную картезианским сомненьем. Он предположил, что все его убеждения ложны, поэтому их надо проверить.
Как Декарт перепроверил свои убеждения
Он решил действовать кардинально, проведя аналогию с корзиной фруктов. Чтобы отделить гниль от хороших плодов, следует все содержимое высыпать, а затем положить в нее лишь уцелевшие экземпляры. Проверку ученый начал с эмпирических убеждений, то есть тех, которые подтверждаются органами чувств.
Декарт пришел к выводу, что слух, зрение, обоняние, осязание не могут гарантировать верность убеждений. Философ привел множество примеров, доказывающих этот факт. Когда человек болен, еда кажется горькой. Руки после игры в снежки ощущают воду комнатной температуры как горячую.
Декарт продолжил рассуждения. В таком случае способен ли спящий осознать ирреальность сновидений? Да, как только индивид просыпается, он понимает, что это был всего лишь сон. Такое сомнение, которое можно развеять, сверившись с собой, он назвал локальным.
Глобальное сомнение
Затем ученый предположил, что вся окружающая реальность ложная. Все вокруг не такое, каким воспринимается (как в «Матрице»). Сомнение, при котором человек не может выйти за его границы и перепроверить, было названо глобальным. Декарт выдвинул гипотезу о существовании злобного гения, который мог создать иллюзорный мир и запереть в нем людей. Философ понимал невероятность наличия такого существа, но он не мог обнаружить и доказательств его отсутствия.
Все вокруг не такое, каким воспринимается (как в «Матрице»). Сомнение, при котором человек не может выйти за его границы и перепроверить, было названо глобальным. Декарт выдвинул гипотезу о существовании злобного гения, который мог создать иллюзорный мир и запереть в нем людей. Философ понимал невероятность наличия такого существа, но он не мог обнаружить и доказательств его отсутствия.
Отчаявшийся ученый все-таки нашел выход. Он понял, что может сомневаться во всем кроме того, что сомневается, то есть мыслит. А если есть мысль, то существует и реальный мыслитель. Так родилась знаменитая декартовская фраза: «Я мыслю, следовательно, существую».
Текст полностью:
https://zen.yandex.ru/media/philosophy/kartezianskoe-somnenie-dekarta-otrajenie-idei-filosofa-v-filme-matrica—5adafaadbcf1bccf58fb4d97
РЕНЕ ДЕКАРТ И ЗЛОЙ ДЕМОН. «Матрица» как философия
КАК МЫ МОЖЕМ ОКАЗАТЬСЯ В МАТРИЦЕ: РЕНЕ ДЕКАРТ И ЗЛОЙ ДЕМОН
Гипотеза, гласящая, что мир, который мы видим, слышим и осязаем, может оказаться иллюзией, развивается сторонниками философского направления под названием скептицизм. Скептики утверждают, что мы не можем с уверенностью утверждать, существует ли внешний мир. Подобно героям «Матрицы», замечающим в привычном мире подозрительные вещи, они отстаивают мнение, что наши знания о мире могут быть поставлены под сомнение.
Скептики утверждают, что мы не можем с уверенностью утверждать, существует ли внешний мир. Подобно героям «Матрицы», замечающим в привычном мире подозрительные вещи, они отстаивают мнение, что наши знания о мире могут быть поставлены под сомнение.
Гипотезы скептицизма особенно популярны у двух групп людей. Первая — это молодые люди, чей подростковый бунт против простых истин, навязываемых родителями, иногда принимает метафизическую форму, толкая их на заявления вроде «Ничто не является тем, чем кажется!» или «Только я знаю, какова реальность на самом деле!».
Вторая и более важная группа — это философы, которые, в свою очередь, тоже делятся на две группы. К первой группе относятся философы, еще не переросшие стадию «метафизического бунта» и поэтому находящие изучение абсурдных и заведомо ложных гипотез увлекательным и приятным занятием. Философы этой группы могут даже открыто признавать лозунги молодых скептиков вполне убедительными. Для нас же сейчас важна вторая группа философов. Она включает в себя тех, кто, подобно Декарту, считает сценарии, подобные «Матрице», полезным инструментом для исследования фундаментальных проблем знания и реальности.
В классическом труде «Размышления о первой философии» Декарт излагает наиболее существенные аргументы скептицизма, которые должны создать для науки прочную базу. Декарт начинает «Размышления» объявлением о намерении считать недействительными все мнения, которые он сможет поставить под сомнение. Абсолютно верными могут считаться только те мнения, которые пройдут проверку Декарта, и только эти взгляды могут служить надежным научным фундаментом. Радикальное сомнение Декарта является методологическим, то есть оно предназначено служить интеллектуальным целям. Вряд ли Декарт действительно стал бы отрицать все взгляды, которые подвергал проверке; их «недействительность» была лишь временной, эвристическим приемом.
Первыми объявляются недействительными те мнения, которые Декарт считает основанными на чувственном восприятии.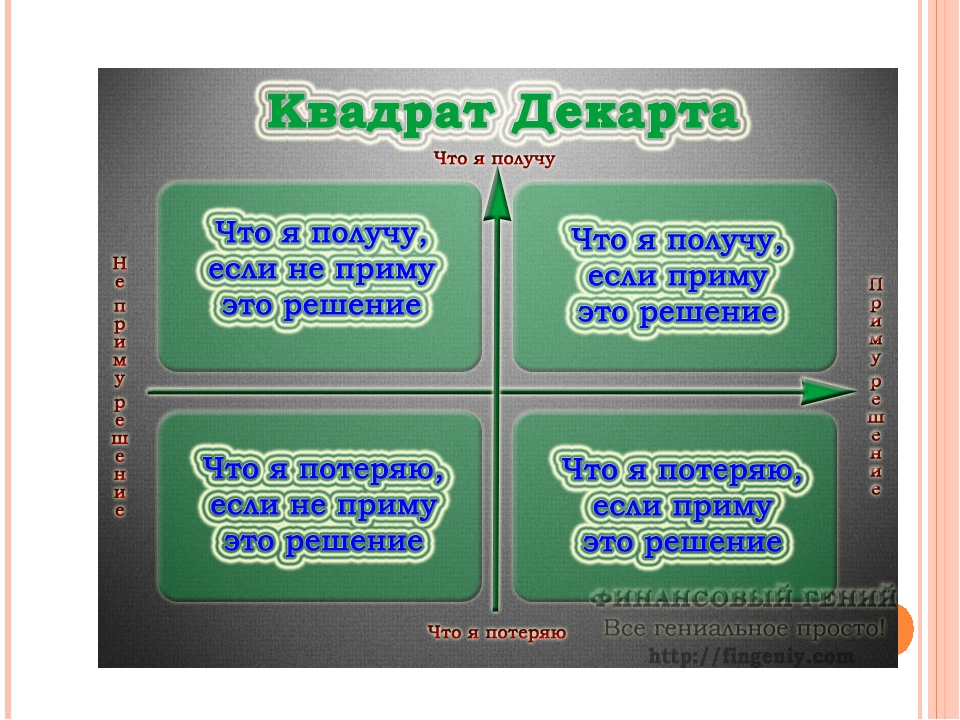 Мы часто подкрепляем свое мнение информацией, полученной посредством зрения, слуха, обоняния и вкуса. Например, мы убеждены, что наш сосед по комнате Йон вернулся с занятий, если видим, как он приближается к дому, и если слышим, как он возится с дверью, то верим, что он снова не может отпереть замок. Однако Декарт отмечает: «Я иногда замечал, что они [чувства] нас обманывают». Это особенно верно в отношении очень маленьких или очень удаленных объектов. Фигура, которую мы принимаем за Йона, может оказаться вором; копошение у дверей может оказаться попыткой вора взломать замок. Из-за того что чувства иногда нас подводят, многие наши суждения, подкрепляемые свидетельством чувств, не удовлетворяют высоким стандартам Декарта, вследствие чего он их отбрасывает.
Мы часто подкрепляем свое мнение информацией, полученной посредством зрения, слуха, обоняния и вкуса. Например, мы убеждены, что наш сосед по комнате Йон вернулся с занятий, если видим, как он приближается к дому, и если слышим, как он возится с дверью, то верим, что он снова не может отпереть замок. Однако Декарт отмечает: «Я иногда замечал, что они [чувства] нас обманывают». Это особенно верно в отношении очень маленьких или очень удаленных объектов. Фигура, которую мы принимаем за Йона, может оказаться вором; копошение у дверей может оказаться попыткой вора взломать замок. Из-за того что чувства иногда нас подводят, многие наши суждения, подкрепляемые свидетельством чувств, не удовлетворяют высоким стандартам Декарта, вследствие чего он их отбрасывает.
Продолжая эксперимент, Декарт указывает, что даже такие относительно неоспоримые суждения, как, например, то, что вы сидите в кресле и читаете эту книгу, могут быть подвергнуты сомнению. Конечно, эти суждения кажутся более надежными, чем ваши догадки о Йоне и о том, что он делает на крыльце. Однако Декарт подчеркивает, что мы часто заблуждаемся в отношении именно таких вещей во сне. Во сне вы можете видеть, что сидите на стуле и читаете эту книгу, хотя на самом деле вы лежите в кровати и у вас быстрая фаза сна. Мы не можем отличить опыт бодрствования от опыта, который мы якобы переживаем во сне, пока не проснемся, Морфеус поддерживает это мнение:
Однако Декарт подчеркивает, что мы часто заблуждаемся в отношении именно таких вещей во сне. Во сне вы можете видеть, что сидите на стуле и читаете эту книгу, хотя на самом деле вы лежите в кровати и у вас быстрая фаза сна. Мы не можем отличить опыт бодрствования от опыта, который мы якобы переживаем во сне, пока не проснемся, Морфеус поддерживает это мнение:
Ты когда-нибудь видел такой сон, Нео, когда был уверен, что это не сон? Что, если ты бы не мог очнуться от этого сна? Как бы ты узнал разницу между миром твоего сна и реальным миром?
На основе своего «сонного» аргумента Декарт делает вывод, что чувственный опыт — не самый надежный механизм проверки, поэтому он отбрасывает все убеждения, сформированные на основе чувственного опыта.
Затем Декарт продолжает наступление на привычные взгляды. Давая нам повод усомниться в представлениях о физическом мире, «сонный» аргумент, кажется, должен оставлять нетронутыми, например, представления о геометрических фигурах. Как пишет Декарт, «ибо сплю ли я или бодрствую, два плюс три дают пять, а квадрат не может иметь более четырех сторон». Однако Декарт заканчивает свое первое «Размышление» рассмотрением следующего, еще более радикального мысленного эксперимента. Он предполагает, что «не всеблагой Бог, источник истины, но какой-то злокозненный гений, очень могущественный и склонный к обману, приложил всю свою изобретательность к тому, чтобы ввести меня в заблуждение».[28] Такое существо, по словам Декарта, могло бы легко изменить наше мнение о сумме двух и трех или о числе сторон квадрата. Еще проще этому злому демону было бы заставить нас думать, что существует внешний для нас физический мир, в то время как на самом деле «я буду мнить небо, воздух, землю, цвета, очертания, звуки и все вообще внешние вещи всего лишь пригрезившимися мне ловушками, расставленными моей доверчивости усилиями этого гения». Отсюда Декарт делает вывод: «…я буду рассматривать себя как существо, лишенное рук, глаз, плоти и крови, каких-либо чувств».
Как пишет Декарт, «ибо сплю ли я или бодрствую, два плюс три дают пять, а квадрат не может иметь более четырех сторон». Однако Декарт заканчивает свое первое «Размышление» рассмотрением следующего, еще более радикального мысленного эксперимента. Он предполагает, что «не всеблагой Бог, источник истины, но какой-то злокозненный гений, очень могущественный и склонный к обману, приложил всю свою изобретательность к тому, чтобы ввести меня в заблуждение».[28] Такое существо, по словам Декарта, могло бы легко изменить наше мнение о сумме двух и трех или о числе сторон квадрата. Еще проще этому злому демону было бы заставить нас думать, что существует внешний для нас физический мир, в то время как на самом деле «я буду мнить небо, воздух, землю, цвета, очертания, звуки и все вообще внешние вещи всего лишь пригрезившимися мне ловушками, расставленными моей доверчивости усилиями этого гения». Отсюда Декарт делает вывод: «…я буду рассматривать себя как существо, лишенное рук, глаз, плоти и крови, каких-либо чувств». Прочитав первое «Размышление» Декарта, сложно представить доказательства того, что наша жизнь не является грандиозным обманом, сотворенным злым демоном. Как же мы можем оспорить скептические аргументы, выдвинутые Декартом?
Прочитав первое «Размышление» Декарта, сложно представить доказательства того, что наша жизнь не является грандиозным обманом, сотворенным злым демоном. Как же мы можем оспорить скептические аргументы, выдвинутые Декартом?
Те, кто видел «Матрицу», могут задать себе еще один вопрос: можем ли мы исключать возможность того, что наши жизни, кажущиеся исполненными смысла, на самом деле лишь иллюзии, созданные в наших мозгах умными компьютерами?
Как Декарт победил Матрицу
Вы – рабы. Рабы инстинктов и рефлексов, электрических процессов своего мозга, химических процессов своего организма. Как заложники компьютерной иллюзии из фильма «Матрица» вы не управляете собой. Это вами управляют.
Именно такой вывод можно сделать (и многие его делают!), когда читаешь статьи о последних научных открытиях в области изучения человеческого мозга, эволюционной психологии и пр. Но неужели правда, что вся наша свобода – просто иллюзия, а люди – только пешки в непознаваемой игре природы?
Но неужели правда, что вся наша свобода – просто иллюзия, а люди – только пешки в непознаваемой игре природы?
На этот вопрос в проекте Академия «Фомы» отвечает Александр Доброхотов, доктор философских наук, ординарный профессор Высшей школы экономики.
Вопрос о свободе — вечная философская проблема — сегодня снова широко обсуждается в связи с рядом новых научных открытий. Иллюзорна свобода или нет? Чтобы понять это, я позволю себе сделать шаг назад – в историю философии.
Когда возникает иллюзия? Когда есть некоторое начальное представление о предмете — и последующая интерпретация, которая опровергает то, что нам казалось истинным изначально. Например, я вижу, что рельсы у горизонта сходятся в одну линию. Это мое первое представление. Однако ученый тут же объяснит мне, что оно неверно, что это всего лишь оптическая иллюзия, и рельсы на самом деле параллельны.
Мы видим, что палка в воде кажется сломанной, что Солнце вращается вокруг Земли, но наука разоблачает эти иллюзии.
Однако именно здесь-то и нужно осознать то, что поняли философы: существуют такие основоположения, которые просто не могут быть иллюзорными. В них нет этой двойственности, нет второго, скрытого от нас плана.
Так Рене Декарт (знаменитый французский философ XVII века), в поисках такого изначального и предельного основоположения вывел свое знаменитое: «мыслю, следовательно существую» (когито эрго сум). Ведь не может быть ложным тот факт, что я мыслю. Для того чтобы сделать такую мысль ложной, ее уже нужно помыслить.
И даже если я стану отрицать свободу, в самом факте такого отрицания осуществится свободный акт.
«Ты веришь в судьбу, Нео?»
В том же ключе рассуждал и блаженный Августин («О Граде Божьем», кн. XI, 26), который, отвечая скептикам, подвергающим всё — и даже человеческое познание — сомнению, указывал, что в самом акте сомнения содержится положительное, истинное высказывание. Я уверен в том, что сомневаюсь. Декларируя сомнение, я делаю это без сомнения. Я утверждаю это. Так само сомнение для Августина и Декарта доказывает что, человек способен мыслить положительно, плодотворно, и этого у него не отнимешь.
Я уверен в том, что сомневаюсь. Декларируя сомнение, я делаю это без сомнения. Я утверждаю это. Так само сомнение для Августина и Декарта доказывает что, человек способен мыслить положительно, плодотворно, и этого у него не отнимешь.
Но Декарт идет дальше и вводит последнее, предельное допущение. Можно ли предположить, что вся реальность этого мира, всё, что мы видим, о чем думаем, к чему стремимся, – все это лишь ловко сконструированный обман какого-то злого духа? Конечно, говорит философ. Но для этого все равно нужно некое «я» — тот, кого этот демон обманывает, или тот, кому снится этот сон. И этот «кто-то» существует, мыслит.
При этом осознание самого себя в принципе не может быть иллюзорным. Почему?
Да потому что тогда демон должен был бы «инсталлировать» в нас эту иллюзию, то есть наше сознание должно было бы быть некой доступной для вторжения идеальной машиной, производящей цепочку ментальных операций. Но сама возможность духовной беззащитности человека перед манипуляциями превосходящих его сознание сил привела Декарта в состояние религиозного ужаса. Ведь выражение «злой демон» является лишь псевдонимом гипотезы «злого Бога», которая изображает мир как тотальную власть злого сверхразума. В самом деле, а что если Бог – злой? Это же предельный ужас!
Ведь выражение «злой демон» является лишь псевдонимом гипотезы «злого Бога», которая изображает мир как тотальную власть злого сверхразума. В самом деле, а что если Бог – злой? Это же предельный ужас!
Разгадку мы уже знаем: само сомнение – несомненно – доказывает бытие самосознания. Самосознание абсолютно бессодержательно, и именно его пустота – защита от возможной фальсификации, подделки: содержания просто нет, а есть только ничем не обусловленное бытие. То есть свобода.
Но злой демон, который так страшил Декарта, был не просто абстрактной моделью. Декарт находился в начале того процесса, который сегодня, кажется, все-таки выдохся: превращения мира в исчисляемую предметность, полностью контролируемую научным рассудком. И именно Декарт открыл предел внушаемости, за который не перейти ни демону (потому что он не сможет), ни Богу (потому что Он не хочет). Сознание не имеет предметного содержания, поэтому никакое содержание не может быть в него вложено, как программа в компьютер.
Но даже если мы допустим ситуацию прямого «инсталлирования» туда какой-либо информации, сам акт самосознания или присвоит себе это «внушенное» содержание, беря ответственность на себя (и тогда демон потеряет над ним власть), или отвергнет его.
Другими словами, демон может внушить все, кроме самосознания.
Gabriel Kronisch
Отсюда, кстати, вытекает и другое следствие: непрозрачность для нас чужого «я». Наша мысль, направленная на чужое «я», схватывает лишь внешние его проявления.
И это чрезвычайно важно: именно благодаря такой непрозрачности возможно настоящее общение, когда личности свободно открывают себя друг другу и нет необходимости превращать другого в «вещь», чтобы понять его.
Итак, никакие биологические процессы или социальные условия не могут определить или ограничить нашу свободу. Потому что человеческая свобода сама себя порождает и обосновывает. Она в принципе не может быть иллюзорной.
Здесь уместно вспомнить великого детерминиста Спинозу. Он утверждал: если бы летящий камень думал, он мог бы подумать, что летит свободно, тогда как на самом деле он летит детерминировано, по закону природы. И в этом резкое отличие Спинозы от Декарта, который сказал бы: если камень действительно подумал, что он свободен – он стал свободен.
Он утверждал: если бы летящий камень думал, он мог бы подумать, что летит свободно, тогда как на самом деле он летит детерминировано, по закону природы. И в этом резкое отличие Спинозы от Декарта, который сказал бы: если камень действительно подумал, что он свободен – он стал свободен.
via GIPHY
Ведь свобода существует именно как действие, как поступок. Ее «исполняют». Никакие заданные условия не отменяют того, что я определяю себя, и я становлюсь таким в результате моего свободного выбора.
Сейчас эти споры обострились, особенно в связи с современной философией сознания, многие сторонники которой полагают, что если в самом «механизме» психики мы найдем детерминацию, это может вообще отменить свободу.
Но в том-то и дело, что свободу отменить нельзя. Ей не нужны посредники во внешнем мире. Она рождается в тот момент, когда я говорю себе: я свободен.
Читайте также:Христианство сделало человека личностью
На заставке фрагмент фото: marcoverch
Принятие решений и проведение совещаний
Основные темы тренинга
Модуль 1.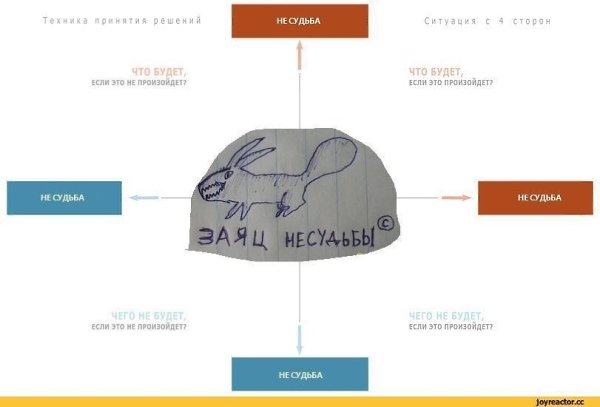 Эффективное решение: типы и стили
Эффективное решение: типы и стили
- Типы управленческих решений
- Алгоритм поиска решения проблемы
- Проблемы при аналитическом принятии решений
- Стили управленческих решений
- Критерии и правила выбора стиля для принятия решений
Модуль 2. Технологии принятия управленческих решений
- Этапы и последовательность процесса принятия решений
- Схема принятия решений в управлении
- Стратегическое планирование
- Стратегическое принятие решений
- Обоснование принимаемых решений и алгоритм их принятия
- Принятие базовых решений
- Технология целеполагания и разработка альтернатив. Постановка целей и задач в формате SMART
- Решения, принимаемые для управления качеством
- Методы эффективного принятия решений: моделирование, ситуационный анализ, SWOT-анализ, групповые
техники принятия решений, метод «Дельфи», матрица Эйзенхауэра, квадрат Декарта и др.
- Типы бизнес-моделей для принятия и анализа решений: концептуальные, структурные и формализованные,
иерархические, графические, функциональные, математические, имитационные модели - Принятие решений в ситуации с неясными последствиями
Модуль 3. Реализация решений и анализ результатов.
- Понятие аналитического управления. Оптимизация решений
- Алгоритм проведения анализа принятых решений
- Контроль решений. Анализ решений в формате диаграмм Ишикавы и Парето
- Критерии выбора эффективных решений
- Подведение итогов. Задания для тренинговых групп
Модуль 4. Эффективное совещание как технология принятия продуктивных решений
- Характеристика деловых совещаний. Цели, задачи и виды совещаний
- Структура и реальные управленческие процессы в ходе проведения совещания
- Основные этапы проведения совещаний
Модуль 5. Групповое взаимодействие в процессе принятия решений
Групповое взаимодействие в процессе принятия решений
- Тип коммуникации между участниками совещания
- Роли участников в процессе проведения совещания
- Чего можно добиться в ходе проведения совещания?
- Негативные стереотипы и ошибки проведения совещания
- Роль и имидж модератора совещания
- Секреты успешного модератора
- Типы «сложных» участников совещания
Модуль 6-7. Формы и методы проведения совещаний в зависимости от целей и задач совещаний
- Оперативные совещания в формате скрам-митинга
- Оперативные совещания в формате Фасилитация Pinpoint
- Оперативные совещания в формате модерации. Методы и техники модерации: «мозговой штурм», «карточный опрос», «mind-mapping», «схема анализа проблемы»
- Оперативные совещания в формате модерации. Базовые правила поведения модератора в зависимости от целей и задач совещаний
- Проблемы, которые решает успешная модерация
- Оперативные совещания в формате «мозгового штурма»: 7 правил, преимущества метода
- 6 креативных методов, используемых для поиска эффективных решений в сочетании с «мозговым штурмом»: метод Киплинга, метод случайных ассоциаций, метод «Feedback for dummie», метод «Porter 5 forces analysis», метод У.
 Диснея, метод Э. Боно «6 думающих шляп»
Диснея, метод Э. Боно «6 думающих шляп»
Модуль 8. Критерии системы принятия эффективных решений
- Критерии системы принятия решений
- Этапы согласования решений
- Принципы принятия эффективных решений.
Продолжительность: 2 дня.
Квадрат Декарта и матрица Эйзенхауэра: разложим всё по клеточкам
Принимать верные решения – это и навык, и опыт, и благосклонность фортуны. Зачастую это происходит интуитивно. Но если непонятно, как принять правильное решение, вас выручат: квадрат Декарта и матрица Эйзенхауэра.
Используя эти приёмы, вы иначе посмотрите на вопрос, ситуацию или сомнение. Если держать их только в голове, складывается однобокое восприятие, на которое сложно повлиять. Но как только вы переносите всё на бумагу, восприятие меняется. Принять правильное решение проще, потому что вы изучили предмет со всех сторон.
Квадрат Декарта
Я не буду углубляться в историю и рассказывать о создателе этого метода. Мы лишь коснёмся практического применения.
Мы лишь коснёмся практического применения.
Вот так выглядит Квадрат Декарта. Четыре поля, в каждом по одному вопросу. Кажется, что вопросы одинаковые. Нет, они скорее перекрученные. Именно поэтому можно докопаться до сути и принять правильное решение.
Вы рассматриваете вопрос с четырёх сторон. Глагол «будет» в квадрате Декарта это не отсылка к будущему. Это обозначение приобретения или потери от того или иного исхода. Чтобы было понятней, пользуйтесь такой трактовкой:
Верхние два квадрата говорят о выгодах. Нижние – об убытках.
Не все приобретения однако ценны, так же как и потери. Поэтому можно присваивать коэффициент со знаком «+» или «–» каждому вписанному пункту. Потом посчитать.
Пока ищете ответы, вы десяток раз прокручиваете информацию в голове, докапываетесь до правды. У вас могут возникнуть новые соображения на этот счёт.
Квадрат Декарта кажется запутанным, когда впервые с ним сталкиваешься. Но уяснив для себя разницу между вопросами, понимаешь, как принять правильное решение.
Матрица Эйзенхауэра
Её прославил Стивен Кови в книге «7 навыков высокоэффективных людей». Матрица Эйзенхауэра помогает разобраться с приоритетами в планировании и постановке целей. Расставить приоритеты – это тоже решение, от которого зависит, насколько грамотно вы распорядитесь временем и усилиями.
Верхняя шкала делит задачи на срочные и не срочные. Слева указана важность. Исходя из двух критериев, вы определяете в какую клеточку отнести каждое дело. Когда разложите все задачи по квадратам, поймёте:
- с чего начать;
- в каком из квадратов больше всего «проводите времени».
- I квадрат вы заполните с лёгкостью, потому что «живёте в нём». Вечные гонки, тушение пожаров, авралы… Знакомо? Вот они, главные гости первой клетки. Многие задачи попадают сюда, потому что вы слишком поздно за них берётесь. И в последний момент, когда сроки горят, вы откладываете всё и занимаетесь почти что простроченными делами. От этого страдает вторая клеточка, а это нехорошо.
 Старайтесь не допускать, чтобы задачи становились одновременно срочными и важными.
Старайтесь не допускать, чтобы задачи становились одновременно срочными и важными. - На фоне первого, II квадрат кажется менее значимым, но это не так. От него зависит ваше развитие и достижение глобальных результатов. «Несрочность» объясняется тем, что такие задачи выполняют на перспективу, обычно регулярно и долго. Чтение, оттачивание навыка, занятия спортом, налаживание связей, следование мечте. Важные, но не срочные дела легко отменить или перенести. Но если относиться так легкомысленно, то ваши достижения через 5 лет не будут кардинально отличаться от сегодняшних. II квадрат – самый приоритетный. Уделяйте ему больше времени, чем другим вместе взятым.
- Срочные, но не важные дела из III квадрата будут вечно вас сопутствовать. По возможности разделывайтесь с ними сразу или поручайте кому-то. Не допустите, чтобы эти дела посягали на время, предназначенное для второй клеточки.
- IV квадрат должен быть пуст. Если задача не срочная и не важная, зачем её заниматься.
Раскидайте планы и цели по матрице и проанализируйте, насколько срочными и важными делами занимаетесь ежедневно.
Для самодисциплины начертите матрицу приоритетов в ежедневнике на неделю вперёд.
Квадрат Декарта и матрица Эйзенхауэра упрощают принятие решений. Пользуйтесь ими постоянно или по необходимости, в зависимости от того, какую пользу и ощущения они вам дают. Но обязательно попробуйте эти приёмы, чтобы понять, как правильно принимать решения.
человек осознает себя через Другого — Моноклер
Рубрики : Избранное, Культура, Переводы, Последние статьи, Психология
«Мыслю, следовательно существую», – постулировал Декарт. Но что такое «Я»? Насколько оно устойчиво и автономно? Способны ли мы существовать и определять себя вне матрицы взаимоотношений? Абиба Бирайн, ученый-когнитивист из Университетского колледжа Дублина, поразмышляла обо всём этом на страницах Aeon, попутно рассказав об африканской философии убунту, брешах в картезианской модели личности, теории диалога Михаила Бахтина, роли Другого в формировании нашего собственного «Я» и бытия, а также о психологических экспериментах, подтверждающих, что в изоляции самосознание человека разрушается.
 Перевели главное.
Перевели главное.Согласно африканской философии убунту, новорождённый ребёнок ещё не человек. Люди рождаются без «эна», или личности, и обретают её только через взаимодействие с внешним миром. Если для западной философской мысли различия между Я и Другими очевидны, в философии убунту границы этих понятий размыты и неопределённы. Джон Мбити, кенийский философ, утверждал:
«Я есть, потому что мы есть, и так как есть мы, существую и я».
Из повседневного опыта мы знаем, что человек в определённой степени формируется обществом, в котором живёт. Отношения с членами сообщества влияют на наше понимание самих себя. Кто «я» относительно других: семьи, друзей, своей культуры, работы и коллег. Мое «я», которое я беру с собой, отправляясь в магазин за продуктами, отличается в своём поведении от того «я», которое, предположим, говорит со своим научным руководителем. Даже самые личные и тайные мысли человека представляют собой переплетение голосов, мнений других людей, в том числе мнений о тебе, неважно, будь это порицание или поощрение.
Пожалуй, идея о неустойчивом, меняющемся и неопределённом «я» может сбить с толку любого. В нашем замешательстве отчасти повинен французский философ Рене Декарт. Он полагал, что человек по природе существо самодостаточное и автономное, рациональное, мыслящее, поэтому он должен подвергать сомнению любое явление внешнего мира, то есть относиться скептически к тому, что находится вне человеческого разума. Несмотря на то, что Декарт не был единственным философом, внесшим вклад в формирование современной теории познания, именно он определил её основные черты.
Декарт поставил перед собой трудную задачу: он хотел найти не связанную с божественной мудростью точку опоры, место, откуда он мог бы увидеть вечные, неизменяющиеся структуры. Согласно Декарту, единственным, на что человек может полагаться в процессе познания, является его собственное «cogito» – способность мыслить, акт сознания. Всё остальное – непостоянно и непредсказуемо. Значит, все процессы и явления внешнего мира (в том числе социальные отношения) не имеют ничего общего с процессом познания себя, процессом обособленным, мыслительным, созерцательным.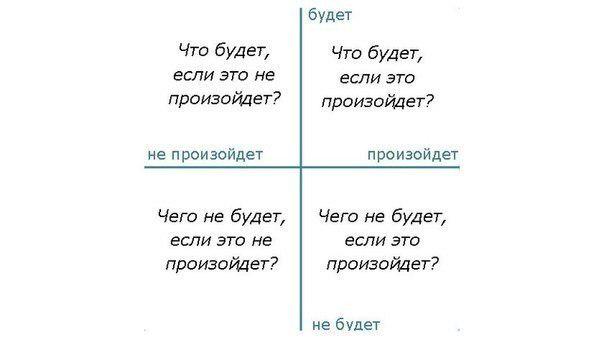
И хотя лишь небольшое число философов и психологов, строгих картезианских дуалистов, утверждало, что материя и разум никак друг с другом не связаны, идея картезианского «cogito» прочно утвердилась в науке. Куда ни посмотри – обнаруживается влияние идей Декарта. Научные эксперименты, изучающие память, часто исходят из посыла, что понятия «я» и «мир» следует разграничивать: если воспоминание живёт только в нашей голове, тогда допустимо переместить человека из его повседневного окружения и вызвать воспоминания в лабораторных условиях, используя флеш-карты и специальные экраны. Человек в этом случае рассматривается как автономное существо, безотносительное к окружению. Память – это то, что имманентно присуще человеку, а не его действие в определённых обстоятельствах.
Читайте также Сартр и Декарт: «Свобода — это единственное основание бытия»
Помимо философии, изучением личности занимается и психология, в частности социальная психология. Но даже в этом случае исследованию подвергается скорее коллектив картезианских субъектов, а не отдельная личность, развивающаяся и эволюционирующая во времени вместе с другими. В 1960-х гг. американские психологи Джон Дарли и Биб Латане заинтересовались обстоятельствами убийства Китти Дженовезе, молодой белой женщины. Преступление было совершено на глазах нескольких человек, по большей части ими были жители окрестных домов, но ни один из них не попытался помешать нападавшему. Учёные провели ряд экспериментов. Так, один из экспериментов заключался в симулировании состояния кризиса, как при эпилептическом припадке, другой — имитировании пожара. В это время Дарли и Латане наблюдали за очевидцами. Результатом стало появление в психологии нового понятия – так называемого «эффекта свидетеля», или «эффекта постороннего». Он характеризуется тем, что неизбежная реакция организма на опасность возникает значительно позднее, если вас окружают другие люди. Психологи предположили, что причиной такого поведения может быть диффузия ответственности, когда чувство личной ответственности распределяется между несколькими членами группы.
В 1960-х гг. американские психологи Джон Дарли и Биб Латане заинтересовались обстоятельствами убийства Китти Дженовезе, молодой белой женщины. Преступление было совершено на глазах нескольких человек, по большей части ими были жители окрестных домов, но ни один из них не попытался помешать нападавшему. Учёные провели ряд экспериментов. Так, один из экспериментов заключался в симулировании состояния кризиса, как при эпилептическом припадке, другой — имитировании пожара. В это время Дарли и Латане наблюдали за очевидцами. Результатом стало появление в психологии нового понятия – так называемого «эффекта свидетеля», или «эффекта постороннего». Он характеризуется тем, что неизбежная реакция организма на опасность возникает значительно позднее, если вас окружают другие люди. Психологи предположили, что причиной такого поведения может быть диффузия ответственности, когда чувство личной ответственности распределяется между несколькими членами группы.
Психолог Франсис Черрив в своей книге The Stubborn Particulars of Social Psychology: Essays on the Research Process (1995) объясняла это другими причинами. По её мнению, такой подход стирает существенную контекстуальную информацию, которая может помочь понять реальные мотивы человека. Так, например, это убийство может быть рассмотрено под другим углом: насилие над женщинами в эти годы не воспринималось всерьёз, и человек отказывался вмешиваться в то, что могло быть обычным бытовым конфликтом. Кроме того, если бы была убита бедная чёрная женщина, то прессу этот случай вообще мог и не заинтересовать.
По её мнению, такой подход стирает существенную контекстуальную информацию, которая может помочь понять реальные мотивы человека. Так, например, это убийство может быть рассмотрено под другим углом: насилие над женщинами в эти годы не воспринималось всерьёз, и человек отказывался вмешиваться в то, что могло быть обычным бытовым конфликтом. Кроме того, если бы была убита бедная чёрная женщина, то прессу этот случай вообще мог и не заинтересовать.
Но есть ли что-то, что может объединить эти две различные формы проявления собственной личности – коллективную, всеобъемлющую и автономную, внутреннюю? Русский философ ХХ века Михаил Бахтин был убеждён, что ответ лежит в диалоге: мне необходим Другой, чтобы создать согласованный, связный образ собственного Я, «утвердить моё бытие, ценностно завершить его. Без Другого меня в полном смысле слова нет». Вспомните те случаи, когда вы ловили себя на мысли, что, например, поэту удалось отразить что-то, что чувствуете именно вы, но никогда не могли выразить это словами; или когда тщетно пытаетесь собраться с мыслями, а они обретают форму только в разговоре с друзьями. Бахтин уверен, что только через общение с другим человеком ты можешь понять свой уникальный взгляд на жизнь и увидеть себя цельной сущностью.
Бахтин уверен, что только через общение с другим человеком ты можешь понять свой уникальный взгляд на жизнь и увидеть себя цельной сущностью.
«Поскольку человек для себя никогда не является целостным и завершённым, то целостно познать его может Другой. Другой может познать меня, а я могу познать Другого».
Смотря на себя через души других, я воплощаю свою внешнюю выраженность. «Истина не рождается и не находится в голове отдельного человека, она рождается между людьми, совместно ищущими истину, в процессе их диалогического общения», – написал Бахтин в своей работе «Проблемы поэтики Достоевского». Ничто не существует вне матрицы взаимоотношений, где это что-то возникло. Напротив, «бытие»- это акт или событие, которое происходит в пространстве между личностью и внешним миром. Согласно этой теории, Другие – решающий фактор в нашем самосознании, что, конечно, дополняет картезианский взгляд на личность.
Углубляемся Экзистенциализм и проблема другого: Сартр и Левинас
Теперь обратимся к двум различным моделям детской психологии — когнитивной и диалогической. Основная идея когнитивной теории Жана Пиаже заключается в реорганизации умственной деятельности ребёнка. Французский психолог отстаивал идею о том, что развивающийся ребёнок должен выступать в роли обособленного ученика, изобретательного учёного, изо всех сил пытающегося самостоятельно познать мир. Диалогические теории, реализованные в таких экспериментах, как исследование кукольного дома Лизы Фрейд (1990), напротив, подчёркивают необходимость взаимодействия между ребёнком и взрослым, последний в свою очередь обеспечивает ребёнка базовыми знаниями о мире, которые становятся некими указательными огоньками на пути познания мира.
Основная идея когнитивной теории Жана Пиаже заключается в реорганизации умственной деятельности ребёнка. Французский психолог отстаивал идею о том, что развивающийся ребёнок должен выступать в роли обособленного ученика, изобретательного учёного, изо всех сил пытающегося самостоятельно познать мир. Диалогические теории, реализованные в таких экспериментах, как исследование кукольного дома Лизы Фрейд (1990), напротив, подчёркивают необходимость взаимодействия между ребёнком и взрослым, последний в свою очередь обеспечивает ребёнка базовыми знаниями о мире, которые становятся некими указательными огоньками на пути познания мира.
Рассмотрим ещё один пример – тюремное заключение в одиночных камерах. Изначально такое наказание задумывалась как способ стимуляции самоанализа, побуждения заключённого к размышлению о совершенном преступлении, как способ обратить его мысли внутрь себя. Итогом всего этого должно было стать его «очищение», признание вины, возвращение в социум. В действительности, экспериментальные данные свидетельствуют, что у людей, содержащихся в одиночном заключении, самосознание распадается. Заключённые переносят физические и психологические трудности, испытывают замешательство, потерянность, беспокойство, искажённое чувство времени, страдают бессонницей. Без внешних контактов, лишённый возможности реализовать свою внутреннюю выраженность, человек рискует потерять себя, исчезнуть в небытии.
Заключённые переносят физические и психологические трудности, испытывают замешательство, потерянность, беспокойство, искажённое чувство времени, страдают бессонницей. Без внешних контактов, лишённый возможности реализовать свою внутреннюю выраженность, человек рискует потерять себя, исчезнуть в небытии.
Постепенно отношение научного сообщества к диалогическим моделям личности меняется, их начинают воспринимать с большей серьёзностью; тем не менее, научная психология изначально ориентирована на индивидуалистическую картезианскую теорию, которая разрывает связь, соединяющую Я одного человека с Другими. Есть зулусская фраза: «Umuntu ngumuntu ngabantu», что означает:
«Человек – только тогда человек, когда существуют другие».
Это точнее говорит о нас, чем декартовское:
«Я мыслю, следовательно – существую».
Статья впервые была опубликована на английском языке в журнале Aeon под заголовком «Descartes was wrong: ‘a person is a person through other persons’».
Обложка: «Диалог», Джулия Маргарет Камерон (1866 г.) / © Wikimedia Commons.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Похожие статьи
Декартово произведение
Литература к занятию 9 — (продолжение)
Язык множеств — декартово произведение
Рассмотрим следующий массив упорядоченных пар чисел, где первое число — это номер строки, а второе число в пара — это номер столбца. Обратите внимание, что заштрихованный прямоугольник находится во втором строка и четвертый столбец представлены упорядоченной парой (2, 4).
(1, 1) | (1, 2) | (1, 3) | (1, 4) | (1, 5) |
(2, 1) | (2, 2) | (2, 3) | (2, 4) | (2, 5) |
(3, 1) | (3, 2) | (3, 3) | (3, 4) | (3, 5) |
Отметим, что в таблице 3 (5) = 15 небольших прямоугольных областей. Мы
разработать эту концепцию с точки зрения набора операций, которые будут
используется для определения умножения.
Мы
разработать эту концепцию с точки зрения набора операций, которые будут
используется для определения умножения.
Заказанная пара: Заказанная пара — это пара объектов, в которой сначала указывается один элемент, а другой элемент обозначен вторым, обозначен ( a , b ).
Декартово произведение: Декартово произведение из двух комплектов A и B , обозначается A × B , это набор всех возможных упорядоченных пар, где элементы A первые и элементы B являются второй.
В обозначении конструктора множеств A × B = {( a, b ): a ∈ A и б ∈ B }.
Пример: Позволять A = {H, T} и B = {1, 2, 3, 4, 5, 6}.
A × В = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5), (Т, 6)}
B × A = {(1, H), (2, H), (3, H), (4, H), (5, H), (6, H), (1, T), (2, T), (3, T), (4, T), (5, T), (6, Т)}
Обратите внимание, что в этом случае A × B ≠ B × А , i. е., декартово
продукт не коммутативен.
е., декартово
продукт не коммутативен.
Также обратите внимание, что n ( A ) ∙ n ( B ) = 2 (6) = 12 = n ( A ) × Б ).
Пример: A × ∅ = ∅ так как никакие упорядоченные пары не могут быть образованы, когда один из наборов пусто.
Также обратите внимание, что n ( A ) ∙ н (∅) = 2 (0) = 0 = n ( A × ∅).
Определение декартова произведения для умножения Целые числа. Пусть А и B — два конечных множества с = n ( A ) и b = n ( B ).Тогда ab = n ( A ´ В ). В номера и и b называются Факторы и ab — это товар.
Два общих метода для Декартово произведение иллюстрируется массивом и деревом. диаграмма.
Пример: Маленький
село имеет четыре улицы и пять проспектов, расположенных в
прямоугольная сетка. Сколько там перекрестков?
Сколько там перекрестков?
У нас есть два набора, улицы ( S ) и проспекты ( A ).Элементы из двух наборов образуют список упорядоченных пар, таких как на пересечении улиц 1 и 2 и Проспект, (1, 2). У нас
4 (5) = n ( S ) ∙ n ( A ) = n ( S × A ) = 20.
В городке двадцать перекрестков.
Пример: In алгебра прямоугольная или декартова координатная плоскость является пример декартова произведения. Мы рассматриваем множество всех упорядоченные пары, описывающие местоположения в плоскости.
Пример: A
пара планирует свадьбу. У них четыре племянницы (Энн,
Бетти, Кэти и Динн) и трех племянников (Эд, Фред и
Гилл). Сколько разных пар можно иметь одного мальчика
и одна девушка в качестве перстень и цветочница?
Сколько разных пар можно иметь одного мальчика
и одна девушка в качестве перстень и цветочница?
Обратите внимание, что эта проблема может рассматриваться либо как проблема повторного сложения, либо как Проблема декартова произведения.
Повторное добавление: Каждая племянница может быть считается набор, содержащий три племянника, поэтому 4 (3) = 3 + 3 + 3 + 3 = 12.
Декартово произведение: {(A, E), (A, F), (A, G), (B, E), (B, F), (B, G), (C, E), (C, F), (C, G), (D, E), (D, F), (D, G)}
4 (3) = n (племянницы) ∙ n (племянники) = n (племянницы × племянники) = 12
В У пары есть двенадцать вариантов для одного носителя кольца и одного цветка девочка.
Возврат
на домашнюю страницу Пейля | Миннесота
Государственный университет Мурхед | Математика
Отдел
Позволяет определять декартово произведение / матрицу для заданий сборки (# 15356) · Проблемы · GitLab.
 org / GitLab · GitLab
org / GitLab · GitLabПроблема для решения
Недавно мы представили дочерние / родительские конвейеры (# 16094 (закрыто)), которые позволяют писать собственный код для генерации дочерних / родительских конвейеров — это мощный способ создания любого настраиваемого поведения, но он немного тяжелый для более простых сценариев. где вы просто хотите создать рабочие места для простой матрицы.
Предложение
Мы добавим ключевое слово matrix к parallel , которое является уже существующим ключевым словом, которое обрабатывает распараллеливание заданий:
стеков развертывания:
этап: развернуть
параллельно:
матрица:
- ПРОВАЙДЕР: aws
СТЕК: [мониторинг, приложение1, приложение2]
- ПОСТАВЩИК: ovh
СТЕК: [мониторинг, резервное копирование, приложение]
- ПОСТАВЩИК: gcp
СТЕК: [данные, обработка] Приведенное выше приведет к созданию следующих параллельных заданий:
-
стеков развертывания (PROVIDER = aws; STACK = мониторинг) -
стеков развертывания (PROVIDER = aws; STACK = app1) -
стеков развертывания (PROVIDER = aws; STACK = app2) -
стеков развертывания (PROVIDER = ovh; STACK = мониторинг) -
стеков развертывания (PROVIDER = ovh; STACK = backup) -
стеков развертывания (PROVIDER = ovh; STACK = app) -
стеков развертывания (PROVIDER = gcp; STACK = data) -
стеков развертывания (PROVIDER = gcp; STACK = processing)
Преимущества здесь:
- Это сохраняет ключевое слово
matrix, чтобы избежать проблемы с невозможностью его разумного расширения позже: # 15356 (комментарий 309409940). Да, это немного менее кратко, чем отсутствие ключевого слова, но это очень ясно показывает намерение.
Да, это немного менее кратко, чем отсутствие ключевого слова, но это очень ясно показывает намерение. - Более сложные сценарии могут по-прежнему использовать дочерние / родительские конвейеры, поэтому нам не нужно проектировать это как язык спецификации построения всеохватывающей матрицы.
Кроме того, более простая матрица также поддерживается, когда каждая запись из первого измерения содержит все элементы из второго:
стеков развертывания:
этап: развернуть
параллельно:
матрица:
- PROVIDER: [aws, ovh, gcp]
СТЕК: [мониторинг, приложение1, приложение2] Эта версия создаст:
-
стеков развертывания (PROVIDER = aws; STACK = мониторинг) -
стеков развертывания (PROVIDER = aws; STACK = app1) -
стеков развертывания (PROVIDER = aws; STACK = app2) -
стеков развертывания (PROVIDER = ovh; STACK = мониторинг) -
стеков развертывания (PROVIDER = ovh; STACK = app1) -
стеков развертывания (PROVIDER = ovh; STACK = app2) -
стеков развертывания (PROVIDER = gcp; STACK = мониторинг) -
стеков развертывания (PROVIDER = gcp; STACK = app1) -
стеков развертывания (PROVIDER = gcp; STACK = app2)
Ограничения
- Для MVC общее количество заданий будет ограничено тем же числом, что и
параллельных(в настоящее время 50: https: // docs.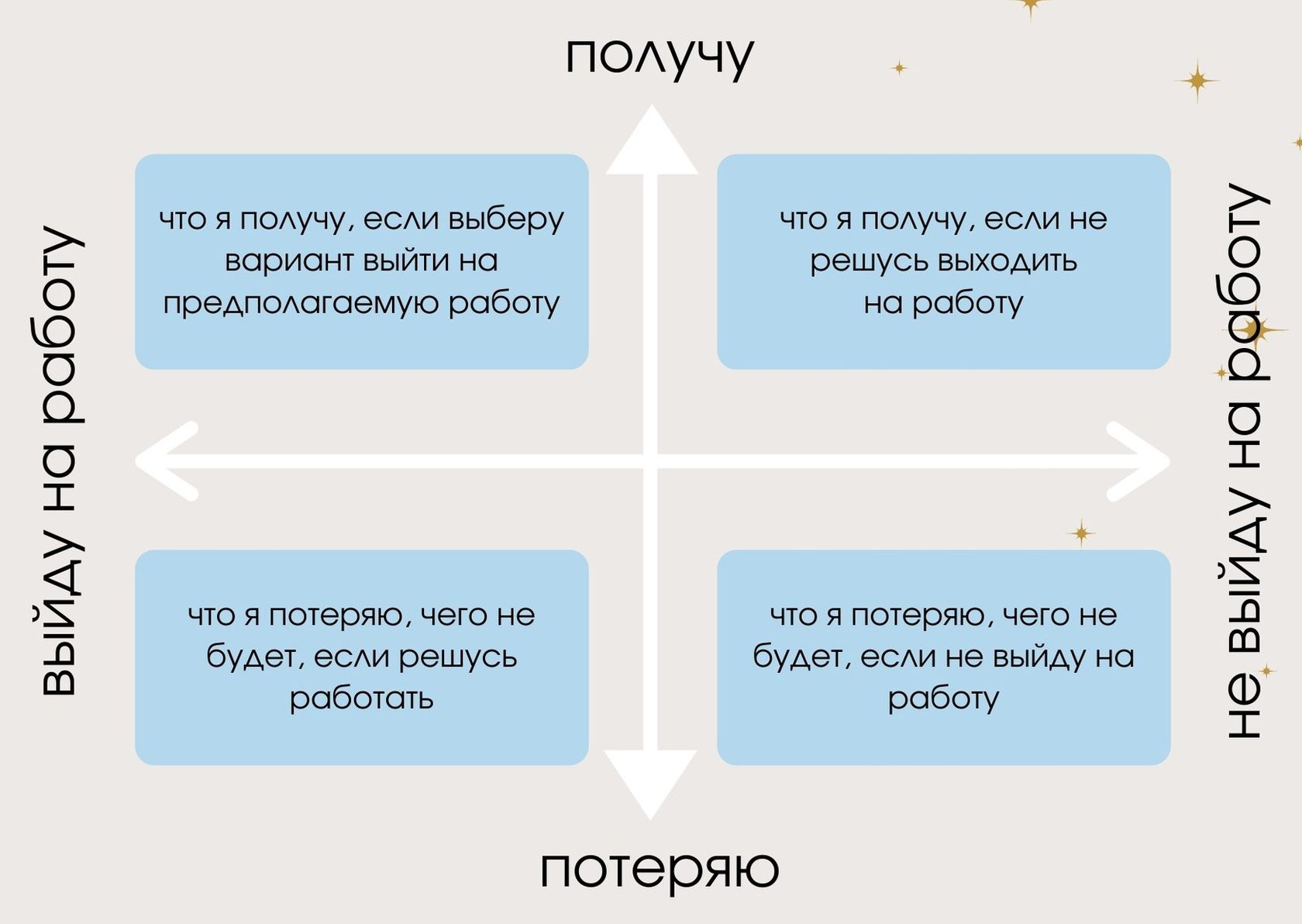 gitlab.com/ee/ci/yaml/#parallel)
gitlab.com/ee/ci/yaml/#parallel) - На сегодняшний день в GitLab не существует такой вещи, как переменная, содержащая массив, поэтому настроить матрицу следующим образом невозможно:
параллельно:
матрица:
- ПРОВАЙДЕР: $ {MY_PROVIDERS}
СТЕК: $ {MY_STACKS} Вместо этого, пока что, чтобы избежать повторения, вы должны использовать extends :
. Матрица
параллельно:
матрица:
- PROVIDER: [aws, ovh, gcp]
СТЕК: [мониторинг, приложение1, приложение2]
строить:
расширяется:.матрица
тест:
расширяется: .matrix
развертывать:
расширяется: .matrix Внешние примеры
Пример .travis.yml
RVM:
- 1. 9.3
- 2.0.0
- 2,2
- рубиновая голова
- Джруби
- рбх-2
- Ри
гемфайл:
- gemfiles / Gemfile.rails-2.3.x
- gemfiles / Gemfile.rails-3.0.x
- gemfiles / Gemfile.rails-3.1.x
- gemfiles / Gemfile.rails-edge
env:
- ИЗОЛИРОВАННЫЕ = правда
- ISOLATED = false
9.3
- 2.0.0
- 2,2
- рубиновая голова
- Джруби
- рбх-2
- Ри
гемфайл:
- gemfiles / Gemfile.rails-2.3.x
- gemfiles / Gemfile.rails-3.0.x
- gemfiles / Gemfile.rails-3.1.x
- gemfiles / Gemfile.rails-edge
env:
- ИЗОЛИРОВАННЫЕ = правда
- ISOLATED = false Это дает 56 индивидуальных рабочих мест.
Пример из реальной жизни предоставлен @MrChrisW:
Travis docs: Построить матрицу
Кроме того, GitHub CI / CD планирует такую же функцию: https: // help.github.com/en/articles/workflow-syntax-for-github-actions#jobsjob_idstrategy
Ссылки по теме
Связанные вопросы https://gitlab.com/gitlab-org/gitlab-ce/issues/13755, https://gitlab.com/gitlab-org/gitlab-ce/issues/19198
Наличие и тестирование
Изменения модульного теста — Да
- Убедитесь, что существующие параллельные ограничения сохранены: требуется минимум 2 задания и максимум 50 экземпляров заданий, а пустые массивы не допускаются.

- Убедитесь, что соответствующие экземпляры задания созданы, как указано в матрице
- Убедитесь, что несколько заданий могут быть выполнены.
расширяетодну и ту же матрицу и количество экземпляров заданий соответственно.
- Убедитесь, что существующие параллельные ограничения сохранены: требуется минимум 2 задания и максимум 50 экземпляров заданий, а пустые массивы не допускаются.
Интеграционные тестовые изменения — не требуются
Смена при сквозном испытании — не требуется
Просмотрите процесс планирования разработки тестирования и обратитесь за помощью к своему коллеге по программному обеспечению в тестировании: https://about.gitlab.com/handbook/engineering/quality/test-engineering/#test-planning
/ cc @MrChrisW @markpundsack @ayufan
комментарий об идентичности и желании в декартовой матрице
Вопрос о сексуальной идентичности широко обсуждается, и ее часто называют спектром. Это означает, что существует только одна переменная, которая изменяется, например, спектр цвета изменяется только с переменной длиной волны. Я предполагаю, что, возможно, это палитра цветов, которые варьируются во множестве переменных и позволяют смешивать оттенки и насыщенность бесконечной природы. В качестве ступеньки к этой палитре я предлагаю матрицу гендерных предпочтений идентичности.
Это означает, что существует только одна переменная, которая изменяется, например, спектр цвета изменяется только с переменной длиной волны. Я предполагаю, что, возможно, это палитра цветов, которые варьируются во множестве переменных и позволяют смешивать оттенки и насыщенность бесконечной природы. В качестве ступеньки к этой палитре я предлагаю матрицу гендерных предпочтений идентичности.
Черновая матрица плоская и основана на декартовой системе, логично, что ее можно было бы расширить до большего количества измерений на основе декартовой методологии.Проект матрицы действительно основан на общепринятом использовании графической терминологии, и любые ограничения этого словаря будут отмечены.
Матрица уклона простирается на расстояние в 1 единицу по каждой оси. Горизонтальная ось представляет гендерную идентичность человека, именно так они называют свой собственный пол. Это может быть набор терминов, но отмеченные точки относятся к мужчине и женщине. Это могут быть цис или транс, но эта терминология не рассматривается в этом проекте, но может быть областью работы в более поздних версиях, с кратким описанием этой темы в конце этого примечания. Вертикальная ось представляет предпочтения человека в интимных отношениях. В идеальном варианте реализации этого чернового варианта матрицы люди будут идентифицироваться по двум переменным, перечисленным по термину, и соответствующей декартовой паре (или более) чисел, представляющих соответствующий графический термин для описания человека. Ключевым моментом, однако, является то, что речь идет не о применении терминов к людям или боксировании с людьми, а о создании общего языка, который позволяет лучше понять богатую и сложную область сексуальной идентичности и выбора образа жизни.Это также показывает, что некоторые, возможно, традиционные представления существуют только в очень маленьких частях черновой матрицы с бесконечно разнообразным набором других возможных терминов.
Вертикальная ось представляет предпочтения человека в интимных отношениях. В идеальном варианте реализации этого чернового варианта матрицы люди будут идентифицироваться по двум переменным, перечисленным по термину, и соответствующей декартовой паре (или более) чисел, представляющих соответствующий графический термин для описания человека. Ключевым моментом, однако, является то, что речь идет не о применении терминов к людям или боксировании с людьми, а о создании общего языка, который позволяет лучше понять богатую и сложную область сексуальной идентичности и выбора образа жизни.Это также показывает, что некоторые, возможно, традиционные представления существуют только в очень маленьких частях черновой матрицы с бесконечно разнообразным набором других возможных терминов.
Для того, чтобы показать полезность графики, будет объяснена некоторая текущая используемая терминология и даны ссылки на то, как она размещается в черновой матрице; есть надежда, что читатели увидят, как это поможет объяснить (при желании) другие комбинации, для которых еще предстоит связать какую-либо соответствующую формулировку.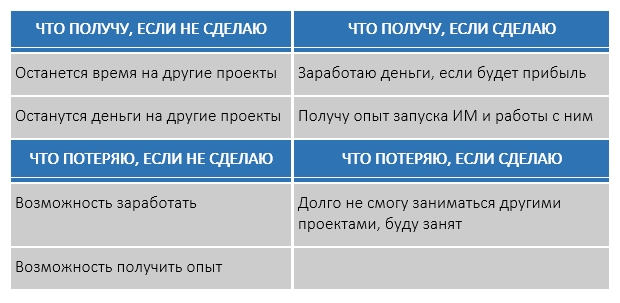 Инициализм LGBTTQQIAAP будет использоваться для этого черновика с некоторыми другими дополнениями.Это ни в коем случае не является исчерпывающим, и если проект матрицы будет принят, возможно, в некоторых ситуациях эти термины больше не понадобятся. Это также решило бы проблему, заключающуюся в том, что некоторые люди, которые не идентифицируют себя как часть сообщества LGBTTQQIAAP +, больше не будут иметь клейма из-за отсутствия терминологии и могут существовать, как и все представители человеческой расы, как часть Матрицы. . Опять же, я подчеркиваю, что речь идет о более подходящей и более гибкой терминологии, а не о том, чтобы ограничивать людей узкими определениями.Также следует отметить, что нынешний словарь не признает, что идентичность и предпочтения являются разными частями человеческой психики и должны рассматриваться как таковые. Существует также некоторая вероятность того, что даже с этими группами идентичность может быть разбита на составные части приписываемых и предполагаемых характеристик; Например, предпочтение можно рассматривать как общедоступную, так и частную информацию.
Инициализм LGBTTQQIAAP будет использоваться для этого черновика с некоторыми другими дополнениями.Это ни в коем случае не является исчерпывающим, и если проект матрицы будет принят, возможно, в некоторых ситуациях эти термины больше не понадобятся. Это также решило бы проблему, заключающуюся в том, что некоторые люди, которые не идентифицируют себя как часть сообщества LGBTTQQIAAP +, больше не будут иметь клейма из-за отсутствия терминологии и могут существовать, как и все представители человеческой расы, как часть Матрицы. . Опять же, я подчеркиваю, что речь идет о более подходящей и более гибкой терминологии, а не о том, чтобы ограничивать людей узкими определениями.Также следует отметить, что нынешний словарь не признает, что идентичность и предпочтения являются разными частями человеческой психики и должны рассматриваться как таковые. Существует также некоторая вероятность того, что даже с этими группами идентичность может быть разбита на составные части приписываемых и предполагаемых характеристик; Например, предпочтение можно рассматривать как общедоступную, так и частную информацию.
Скаляр, Вектор, Матрица
(… и матрицы)
Что такое скаляры и векторы?
Скаляр
имеет только звездную величину (размер):3.044, −7 и 2½ — скаляры
Расстояние, скорость, время, температура, масса, длина, площадь, объем, плотность, заряд, давление, энергия, работа и мощность — все это скаляры.
И обратите внимание на эти специальные слова:
Расстояние от смещения
- Расстояние — скаляр («3 км»)
- Смещение — вектор («3 км к юго-востоку»)
Вы можете пройти большое расстояние, но ваше перемещение может быть небольшим (или нулевым, если вы вернетесь на старт).
Скорость против скорости
- Скорость — это то, насколько быстро что-то движется.
- Скорость — это скорость с направлением .
Говоря, что Собака Ариэль бежит со скоростью , 9 км / ч. (километров в час) — это скорость.
Но сказать, что он бежит 9 км / ч на запад — это скорость.
См. «Скорость» и «Скорость», чтобы узнать больше.
Обозначение
Вектор часто пишется полужирным шрифтом , например a или b , поэтому мы знаем, что это не скаляр:
- , поэтому c — вектор, его величина и направление
- , но c — это скаляр, например 3 или 12.4
Пример: k b на самом деле является скаляром, умноженным на k вектор b .
Вектор также может быть записан как буквы его головы и хвоста со стрелкой над ним, например:
Использование скаляров
Скаляры просты в использовании. Просто относитесь к ним как к обычным числам.
Пример: 3 кг + 4 кг = 7 кг
Использование векторов
На странице, посвященной векторам, есть более подробная информация, но вот краткое изложение:
Мы можем сложить два вектора, соединив их голова к хвосту:
Мы можем вычесть один вектор из другого:
- сначала мы меняем направление вектора, который мы хотим вычесть,
- , затем добавьте их как обычно:
а — б
Мы можем умножить вектор на скаляр (это называется «масштабирование» вектора):
Пример: умножить вектор
m = (7,3) на скаляр 3| a = 3 м = (3 × 7,3 × 3) = (21,9) |
По-прежнему указывает в том же направлении, но в 3 раза длиннее
(И теперь вы знаете, почему числа называются «скалярами», потому что они «масштабируют» вектор вверх или вниз. )
Полярное или декартово
Вектор может быть в:
- величина и направление (полярная) форма,
- или x и y (декартово)
Как это:
| <=> | ||
| Vector a in Polar Координаты | Вектор a в декартовой системе координат Координаты |
(Прочтите, как преобразовать их в полярные и декартовы координаты.)
Пример: вектор
13 под углом 22,6 °В полярной форме (величина и направление):
Вектор 13 под углом 22,6 °
Приблизительно (12,5) В декартовой (x, y) форме:
Вектор (12,5)
Попробуйте векторный калькулятор, чтобы понять, как все это работает.
Умножение вектора на вектор (скалярное произведение и кросс-произведение)
Как умножить два вектора вместе? Есть несколько способов! (Подробнее читайте на этих страницах. |
Более двух размеров
Векторы также отлично работают в трех и более измерениях:
Вектор (1,4,5)
Список номеров
Таким образом, вектор можно рассматривать как список чисел :
- 2 числа для двухмерного пространства, например (4,7)
- 3 числа для трехмерного пространства, например (1,4,5)
- и т. Д.
Скаляры, векторы и матрицы
И когда мы включаем матрицы, мы получаем вот такой интересный паттерн:
- Скаляр — это число, например 3, -5, 0.368 и т.д.,
- Вектор — это список чисел (может быть в строке или столбце),
- Матрица — это массив чисел (одна или несколько строк, один или несколько столбцов).
Фактически вектор также является матрицей ! Потому что матрица может иметь только одну строку или один столбец.
Итак, правила, которые работают для матриц, работают и для векторов.
Спецификация молекулы и геометрии
Координаты
PSI4 имеет очень гибкий анализатор входных данных, который позволяет пользователю предоставлять
геометрии в виде декартовых координат, переменных Z-матрицы или комбинации
обе.Для обоих поддерживается использование фиксированных значений и переменных. За
Например, геометрия для H 2 может быть указана несколькими способами, используя молекула optional_molecule_name {...} block.
или
молекула {
ЧАС
H 1 r
г = 0,9
}
|
или
молекула {
h2
h3 h2 0,9
}
|
или
молекула {
H 0.0 0,0 0,0
В 0,0 0,0 0,9
}
|
или
молекула {
В 0,0 0,0 0,0
H 0,0 0,0 г
г = 0,9
}
|
или
молекула {
H 0,0 0,0 -r
H 0,0 0,0 г
г = 0,45
}
|
Пустые строки игнорируются и, в отличие от обычного синтаксиса Python, отступ внутри
блок молекулы не имеет значения, хотя само ключевое слово молекула должно
быть выровненным внутри ввода в соответствии со стандартным синтаксисом Python. Для большего
примеры задания геометрии, см. входной файл mints1 в примерах
папка. Также возможно смешивать декартову геометрию и геометрию Z-матрицы.
спецификации, как показано на mints4 и
mints6 образцы входных файлов. Например, рассмотрим следующие
спецификация геометрии, взятая из ввода mints6:
Для большего
примеры задания геометрии, см. входной файл mints1 в примерах
папка. Также возможно смешивать декартову геометрию и геометрию Z-матрицы.
спецификации, как показано на mints4 и
mints6 образцы входных файлов. Например, рассмотрим следующие
спецификация геометрии, взятая из ввода mints6:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 год 22 23 24 25 26 27 28 29 30 31 год 32 33 34 | молекула аланина {
N -1.527107413251 0,745960643462 0,766603000356
С -0,075844098953 0,8117041 0,711418672248
С 0,503195220163 -0,247849447550 -0,215671574613
О -0,351261319421 -0,748978309671 -1,0895723
О 1.639498336738 -0.571249748886 -0.174705953194
H -1.207655674855 -0.365 |
Здесь мы удаляем водород из альфа-углерода глицина и заменяем его
с метильной группой. Применение этого патча с использованием декартовых координат является
сложно, потому что это зависит от ориентации существующей единицы глицина.В этом примере мы используем координаты Z-матрицы для определения метильной группы, и
определить ориентацию в терминах существующих декартовых координат глицина
который намного легче визуализировать, чем соответствующий только декартово
подход.
Ключевые слова молекул
Помимо указания геометрии, может быть
предоставленный в блоке молекулы молекула optional_molecule_name {...} .
- Зарядка и множественность
- Если два целых числа
начисление кратностьвстречаются на любом линии блока молекулы, они интерпретируются как заряд молекулы и кратность (\ (2 M_s + 1 \)) соответственно.Для мультифрагментов комплексов, каждый фрагмент может иметьзаряд кратностьлиния. - Шт.
- По умолчанию используются единицы Ангстрема; это изменено добавлением
строка, которая читает
единиц spec, гдеspec— однаанг,ангстрема,у.е.,auилиbohr. - Ориентация
- Для некоторых расчетов требуется, чтобы молекула не переориентировалась.
 Этот
может быть достигнуто добавлением либо
Этот
может быть достигнуто добавлением либо no_reorient, либоnoreorient. Чтобы предотвратить даже повторное центрирование молекулы, добавьтеno_comилиnocom. - PubChem
- Строка, показывающая
pubchem: mol, определяет геометрию молекулымольиз базы данных PubChem, гдемольлибо название молекулы IUPAC или номер CID. См. Базу данных PubChem для Детали. - Симметрия
- Симметрия может быть определена линией, читающей симметрию
Символ, гдесимвол— символ Шёнфлиса (абелевой) точечной группы, используемой для вычислений, один изc1,c2,ci,cs,d2,c2h,c2vилиd2h. Это не нужно указывать, поскольку симметрия молекулы автоматически обнаружен PSI4. Подробнее см. Симметрия.
Подробнее см. Симметрия. - Фрагменты
- Строка
-интерпретируется как разделитель между двумя нековалентно связанные молекулярные фрагменты. Подробнее см. Нековалентно связанные фрагменты молекул.
Множественные молекулы
Для облегчения более сложных вычислений можно дать имя для каждой молекуле и сообщить PSI4, какую из них следует использовать в данном расчет. Например, рассмотрим следующий входной файл:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | молекула h3 {
ЧАС
H 1 0.9
}
установить основу cc-pvdz
установить ссылку rhf
energy ('scf') # на h3
чистый()
молекула h {
ЧАС
}
установить основу cc-pvdz
установить ссылку uhf
energy ('scf') # на H
|
Здесь две отдельные работы выполняются над двумя разными молекулами; первый
выполняется для H 2 , а второй — для атома H. Последняя молекула, которая будет
По умолчанию указана «активная» молекула. Чтобы явно активировать именованный
молекула, предоставляется команда активации. С его помощью указанный выше входной файл может быть
эквивалентно записывается следующим образом.В качестве альтернативы молекула может быть указана
непосредственно к вычислительной функции. Ниже третий расчет такой же, как
первый.
Чтобы явно активировать именованный
молекула, предоставляется команда активации. С его помощью указанный выше входной файл может быть
эквивалентно записывается следующим образом.В качестве альтернативы молекула может быть указана
непосредственно к вычислительной функции. Ниже третий расчет такой же, как
первый.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 год 22 23 24 25 26 27 28 | молекула h3 {
ЧАС
H 1 0,9
}
молекула h {
ЧАС
}
активировать (h3)
установить основу cc-pvdz
установить ссылку rhf
energy ('scf') # на h3
чистый()
активировать (h)
установить основу cc-pvdz
установить ссылку uhf
energy ('scf') # на H
# --------------------------------------
# эквивалент предыдущего ввода заканчивается здесь
чистый()
установить ссылку rhf
energy ('scf', молекулярная = h3) # на h3
|
Ключевые слова управления заданиями предоставляет более подробную информацию об управлении заданиями. и ключевые слова расчета, использованные в приведенных выше примерах.
и ключевые слова расчета, использованные в приведенных выше примерах.
Призрачные атомы
Хотя многие обычные вычисления, в частности SAPT и коррекция противовеса, могут можно значительно упростить, используя обозначения, описанные в разделе «Фрагменты нековалентно связанных молекул», иногда требуется ручное указание призрачных атомов. Либо
молекула he2 {
Он
Gh (He) 1 2,0
}
|
или
молекула he2 {
Он
@He 1 2.0
}
|
будет генерировать димер гелия со вторым призрачным атомом, , то есть , обладающий базисные функции, но без электронов или заряда ядра. См. Dfmp2_1 и призраков для демонстрации обоих механизмов определения призрачные атомы.
Изотопное замещение
Осторожно
Использование изотопного замещения в PSI4 не очень хорошо разработан, и синтаксис может быть изменен.
В настоящее время изотопы могут быть указаны только во время создания молекулы
Синтаксис для воды, замещенной дейтерием и тритием, приведен ниже. Примечание
это асимметричное изотопное замещение, такое как этот , изменит точечная группа симметрии молекулы.
Примечание
это асимметричное изотопное замещение, такое как этот , изменит точечная группа симметрии молекулы.
молекула dto {
ед.
О 0,00000000 0,00000000 0,00000000
[email protected] 0.00000000 1.93042809 -1.10715266
[email protected] 0,00000000 -1,93042809 -1,10715266
}
|
Массы, используемые PSI4, можно найти на psi4 / psi4 / include / psi4 / masses.h. См. Freq-isotope о единственное применение изотопологов в настоящее время в PSI4.
Получение приблизительных начальных предположений геометрии может быть обременительным. Z-матрица
система координат была разработана, чтобы предоставить химикам интуитивно понятный метод для
угадывание структур с точки зрения длин связей и углов. Пока ввод Z-матрицы
интуитивно понятный для небольших молекул с несколькими степенями свободы, он быстро становится
трудоемка по мере роста размера системы. Чтобы получить разумное начальное предположение
геометрия, PSI4 может принимать химическое имя в качестве входных данных; это затем используется
чтобы попытаться получить декартовы координаты из базы данных [PubChem].
Например, чтобы выполнить вычисление бензола, мы можем использовать следующую спецификацию молекулы:
молекула бензола {
pubchem: бензол
}
|
Если компьютер подключен к Интернету, приведенный выше код проинструктирует PSI4 для поиска в PubChem начальной структуры. Поиск действительно выполняется для соединений, имя которых содержит «бензол», поэтому несколько записи будут возвращены. Если указано название («бензол» в приведенном выше example) точно соответствует одному из результатов, эта запись будет использоваться.Если нет найдено точное совпадение результатов, а также уникальный химический идентификатор (CID), печатаются в выходном файле, предлагая пользователю предоставить больше конкретное имя. Например, если мы знаем, что хотим выполнить вычисление на соединение, в названии которого содержится «бензол», но мы не уверены в точном названии ИЮПАК имя, можно использовать следующий ввод:
молекула бензола {
pubchem: бензол *
}
|
Добавление «*» предотвращает обнаружение точного совпадения и, в то время, записи, в выходном файле отображаются следующие результаты:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | Химический идентификатор Название ИЮПАК
241 бензол
7371 бензолсульфоновая кислота
| бензолсульфонат
244 фенилметанол
727 1,2,3,4,5,6-гексахлорциклогексан
240 бензальдегид
65723 бензолсульфоногидразид
74296 N-фенилбензолсульфонамид
289 бензол-1,2-диол
243 бензойная кислота
7370 бензолсульфонамид
636822 1,2,4-триметокси-5 - [(E) -проп-1-енил] бензол
7369 бензолсульфонилхлорид
12932 N- [2-ди (пропан-2-илокси) фосфинотиоилсульфанилэтил] бензолсульфонамид
7505 бензонитрил
78438 N- [анилино (фенил) фосфорил] анилин
12581 3-фенилпропаннитрил
517327 натрия бензолсульфонат
637563 1-метокси-4 - [(E) -проп-1-енил] бензол
252325 [(E) -проп-1-енил] бензол
Обратите внимание, что некоторые из этих результатов не содержат строки «бензол»; эти
у соединений есть синонимы, содержащие этот текст. Теперь мы можем заменить
«Бензол *» во входном файле с одним из вышеуказанных соединений, используя либо
Имя IUPAC или CID, указанный в списке, , а именно :
Теперь мы можем заменить
«Бензол *» во входном файле с одним из вышеуказанных соединений, используя либо
Имя IUPAC или CID, указанный в списке, , а именно :
молекула бензола {
pubchem: 637563
}
|
или
молекула бензола {
pubchem: 1-метокси-4 - [(E) -проп-1-енил] бензол
}
|
Некоторые структуры в базе данных довольно слабо оптимизированы и не имеют правильную симметрию.Перед началом вычислений PSI4 будет проверьте, близка ли молекула к каждому из возможных симметрии и соответствующим образом скорректируют структуру, чтобы используется симметрия.
Стандартные ключевые слова, описанные в разделе «Ключевые слова молекул», могут быть используется вместе для определения заряда, кратности, симметрии для использования, и т. д. .
Симметрия
Для повышения эффективности PSI4 может использовать самую большую абелеву подгруппу полного
точечная группа молекулы. Одновременно ряд количеств, таких как
SOCC и DOCC — это массивы, элементы которых относятся к неприводимым
представления (ререпы) точечной группы молекул. Заказ напольных покрытий
следует соглашению, используемому в Cotton’s Chemical Applications of Group
Теория , подробно описанная в таблице Irreps. Мы ссылаемся на это
в дальнейшем именуется «Заказ хлопка».
Одновременно ряд количеств, таких как
SOCC и DOCC — это массивы, элементы которых относятся к неприводимым
представления (ререпы) точечной группы молекул. Заказ напольных покрытий
следует соглашению, используемому в Cotton’s Chemical Applications of Group
Теория , подробно описанная в таблице Irreps. Мы ссылаемся на это
в дальнейшем именуется «Заказ хлопка».
| Группа точек | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| \ (C_1 \) | \ (А \) | |||||||
| \ (C_i \) | \ (A_g \) | \ (А_у \) | ||||||
| \ (C_2 \) | \ (А \) | \ (В \) | ||||||
| \ (C_s \) | \ (А ‘\) | \ (А ‘\) | ||||||
| \ (Д_2 \) | \ (А \) | \ (B_1 \) | \ (B_2 \) | \ (В_3 \) | ||||
| \ (C_ {2v} \) | \ (A_1 \) | \ (A_2 \) | \ (B_1 \) | \ (B_2 \) | ||||
| \ (C_ {2h} \) | \ (A_g \) | \ (B_g \) | \ (А_у \) | \ (Б_у \) | ||||
| \ (D_ {2h} \) | \ (A_g \) | \ (B_ {1g} \) | \ (B_ {2g} \) | \ (B_ {3g} \) | \ (А_у \) | \ (B_ {1u} \) | \ (B_ {2u} \) | \ (B_ {3u} \) |
Например, вода (симметрия \ (C_ {2v} \)) имеет три дважды занятых \ (A_1 \) орбитали, а также по одной симметрии \ (B_1 \) и \ (B_2 \); то соответствующий массив DOCC поэтому:
Хотя PSI4 определит симметрию автоматически и будет использовать наибольшую
возможна абелева подгруппа, пользователь может захотеть работать в группе с более низкой точкой.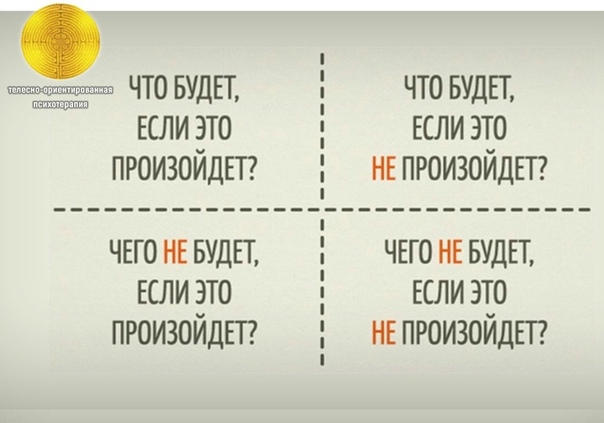 Для этого можно использовать ключевое слово молекулы
Для этого можно использовать ключевое слово молекулы симметрия символ (см. Ключевые слова молекул). В большинстве случаев стандартный
Символ Schönflies (один из c1 , c2 , ci , cs , d2 , c2h , c2v , d2h будет достаточно для символа .
Для некоторых вычислений пользователь может захотеть указать, какие именно
Подгруппа должна использоваться путем добавления уникального спецификатора оси.Например, когда
выполнение вычислений на молекуле с симметрией \ (D_ {2h} \) в \ (C_ {2v} \),
Ось \ (C_2 \) может быть выбрана как \ (x \), \ (y \) или \ (z \); они могут
можно указать, запросив симметрию как c2vx , c2vy или c2vz соответственно.
Аналогично c2x , c2y , c2z , c2hx , c2hy и c2hz ярлыки действительны. Для симметрии \ (C_s \) метки csx , csy и csz запрашивает, чтобы плоскости \ (yz \), \ (xz \) и \ (xy \) использовались в качестве зеркальной плоскости,
соответственно. 2B_2 \) являются возбужденными состояниями, которые подвержены
вариационный коллапс. Один из способов получить надежные энергии для этих состояний — это
использовать метод с несколькими состояниями; в этом случае проще запустить весь
вычисление в самой низкой симметрии, необходимое во время конечной разности
процедура.
2B_2 \) являются возбужденными состояниями, которые подвержены
вариационный коллапс. Один из способов получить надежные энергии для этих состояний — это
использовать метод с несколькими состояниями; в этом случае проще запустить весь
вычисление в самой низкой симметрии, необходимое во время конечной разности
процедура.
Нековалентно связанные фрагменты молекул
PSI4 имеет широкий спектр инструментов для лечения нековалентных межмолекулярные силы, включая коррекцию противовеса и адаптированную симметрию методы теории возмущений.Это требует определения того, какие фрагменты взаимодействуют внутри комплекса. PSI4 предоставляет очень простой механизм для этого: просто определите геометрию комплекса, используя стандартные Декартова, Z-матрица или их смесь, спецификации, а затем поместите два прочерки между несвязанными фрагментами. Например, чтобы изучить взаимодействие энергии молекул этана и этина, мы можем использовать следующую молекулу блок:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | молекула енина {
0 1
С 0. |
В этом случае заряд и кратность каждого взаимодействующего фрагмента равны явно указано. Если указаны начисление и кратность первый фрагмент, предполагается, что он одинаков для всех фрагментов.Когда учитывая взаимодействующие фрагменты, общий заряд — это просто сумма всех заряды фрагментов, и предполагается, что любые неспаренные электроны связаны с дает максимально возможное значение \ (M_s \).
Определив молекулу, содержащую фрагменты, подобные eneyne выше, она
просто выполнить вычисления только на подмножестве
фрагменты. Например, приведенные ниже команды сначала запускают scf на этене.
только фрагмент ( extract_subsets (1) извлекает фрагмент 1 как реальные атомы
и отбрасывает оставшиеся фрагменты), а затем — этеновый фрагмент с
фантомный фрагмент этина ( extract_subsets (1,2) извлекает фрагмент 1 как
Реальные атомы и устанавливает фрагмент 2 как призрачные атомы). За пределами бимолекулярной
могут использоваться комплексы, массивы, например
За пределами бимолекулярной
могут использоваться комплексы, массивы, например extract_subsets (2, [1,3]) :
мА = eneyne.extract_subsets (1)
энергия ('scf')
чистый()
mAcp = eneyne.extract_subsets (1,2)
энергия ('scf')
|
Если молекула содержит фрагменты, но не имеет удобного расположения для –, можно применить функцию auto_fragments () , как показано на
pywrap-base, чтобы вернуть в качестве активной молекулы предыдущую
активная молекула, только фрагментированная.
Продвинутый Python
Именованная молекула во входном файле является полноценным экземпляром
мощный класс C ++ Molecule . Таким образом, все участники
функции (которые были экспортированы через pybind11), задокументированные там
доступны через ручку option_molecule_name in молекула необязательное_имя_молекулы {...} .
Геометрия молекулы может быть получена, установлена и обработана как
Матрицаобъект.Ниже показано, как получить доступ координаты во входном файле в Python.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 год 22 23 24 25 26 27 28 29
молекула формальдегида { С 0,0 0,0 0,0 О 0,0 1,2 0,0 В -0,8 -0,3 0,0 H 0,8 -0,3 0,0 # установить геометрию в ангстремах } Formaldehyde.update_geometry () # обновляем внутреннюю структуру молекулы с момента вызова pre-energy () formdehyde.print_out () # выводить молекулу в выходной файл geom1psi = формальдегид.geometry () # получить координаты в боре как psi4.Matrix geom1psi.print_out () # выводить массив координат в выходной файл geom1py = mat2arr (geom1psi) # получить координаты в виде массива Python print geom1py # вывести координаты на экран geom2py = [[0,0, 0,0, 0,0], [0,0, 1,5, 0,0], [-0,8, -0,3, 0,0], [0.8, -0.3, 0.0]] # определяем альтернативные координаты в ангстремах как массив Python geom2psi = psi4.Matrix (4, 3) # инициализировать psi4.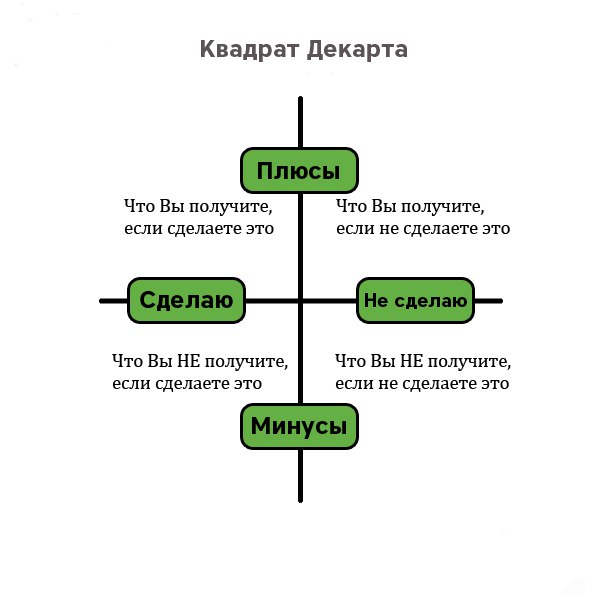 Матрица
geom2psi.set (geom2py) # загружаем массив Python в psi4.Matrix
geom2psi.scale (1.0 / psi_bohr2angstroms) # масштабировать в бор
geom2psi.print_out () # выводить альтернативный массив координат в выходной файл
формальдегид.set_geometry (geom2psi) # загрузить альтернативные координаты в молекулу
формальдегид.update_geometry () # обновить внутреннюю структуру молекулы
formdehyde.print_out () # вывод новой молекулы в выходной файл
compare_values (28,9950517332, формальдегид.Nuclear_repulsion_energy (), 4, "geom2 забрал")
Матрица
geom2psi.set (geom2py) # загружаем массив Python в psi4.Matrix
geom2psi.scale (1.0 / psi_bohr2angstroms) # масштабировать в бор
geom2psi.print_out () # выводить альтернативный массив координат в выходной файл
формальдегид.set_geometry (geom2psi) # загрузить альтернативные координаты в молекулу
формальдегид.update_geometry () # обновить внутреннюю структуру молекулы
formdehyde.print_out () # вывод новой молекулы в выходной файл
compare_values (28,9950517332, формальдегид.Nuclear_repulsion_energy (), 4, "geom2 забрал")
Молекулы могут быть инициированы из файлов XYZ и фрагментированы для вычислений SAPT.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 год 22 23 24 25 26 27 28 29 30 31 год 32 33 34 35 год 36 37 38 39
# >>> кошка mol1.xyz # 7 # #O 0.00000000 -0.05786571 -1.47979303 #N 0.00000000 0.01436394 1.46454628 #H 0.00000000 0,82293384 -1,85541474 #H 0.81348351 0.
 39876776 1.92934049
#H 0.00000000 0.07949567 -0.51934253
#H 0.00000000 -0.98104857 1.65344779
#H -0,81348351 0,39876776 1,92934049
# >>> кот mol2.xyz
# 6 а.е.
# вещи
# C 0.00000000000000 0.00000000000000 5.26601138679877
# C 0.00000000000000 0.00000000000000 -3.15195886530135
# H 0.00000000000000 0.00000000000000 7.28558683837122
# H 0.00000000000000 0.00000000000000 -1.12178201232889
# N 0.00000000000000 0.00000000000000 3.08339310458383
# N 0.00000000000000 0.00000000000000 -5.33865984413460
sapt = {'mol1': -0,0105313323529,
'mol2': -0.00839486625709}
nre = {'mol1': 38.8138764635,
'mol2': 72.3451968428}
установить основу jun-cc-pvdz
для моль в ['моль1', 'моль2']:
filen = mol + '.xyz'
p4mol = Molecule.init_with_xyz (filen) # создать молекулу из файла выше
fragmentedmol = auto_fragments (Molele = p4mol) # фрагмент с алгоритмом BFS
activate (fragmentedmol) # активировать возвращенную молекулу (для sapt)
e = energy ('sapt0') # запускаем SAPT, который требует 2 фрагмента
compare_values (sapt [моль], e, 5, '% s sapt ok'% моль)
compare_values (nre [моль], p4 моль.
39876776 1.92934049
#H 0.00000000 0.07949567 -0.51934253
#H 0.00000000 -0.98104857 1.65344779
#H -0,81348351 0,39876776 1,92934049
# >>> кот mol2.xyz
# 6 а.е.
# вещи
# C 0.00000000000000 0.00000000000000 5.26601138679877
# C 0.00000000000000 0.00000000000000 -3.15195886530135
# H 0.00000000000000 0.00000000000000 7.28558683837122
# H 0.00000000000000 0.00000000000000 -1.12178201232889
# N 0.00000000000000 0.00000000000000 3.08339310458383
# N 0.00000000000000 0.00000000000000 -5.33865984413460
sapt = {'mol1': -0,0105313323529,
'mol2': -0.00839486625709}
nre = {'mol1': 38.8138764635,
'mol2': 72.3451968428}
установить основу jun-cc-pvdz
для моль в ['моль1', 'моль2']:
filen = mol + '.xyz'
p4mol = Molecule.init_with_xyz (filen) # создать молекулу из файла выше
fragmentedmol = auto_fragments (Molele = p4mol) # фрагмент с алгоритмом BFS
activate (fragmentedmol) # активировать возвращенную молекулу (для sapt)
e = energy ('sapt0') # запускаем SAPT, который требует 2 фрагмента
compare_values (sapt [моль], e, 5, '% s sapt ok'% моль)
compare_values (nre [моль], p4 моль. Nuclear_repulsion_energy (), 4, '% s ok'% моль)
clean () # чистая царапина между вычислениями цикла
Nuclear_repulsion_energy (), 4, '% s ok'% моль)
clean () # чистая царапина между вычислениями цикла
Доступна информация об основных элементах, массе и координатах молекулы
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 год 22 23 24 25 26 27 28 29 30 31 год 32 33 34 35 год 36 37 38 39 40 41 год 42 43
молекула енина { 0 1 C_ene 0,000000 -0.667578 -2.124659 C_ene 0,000000 0,667578 -2,124659 [email protected] 0.923621 -1.232253 -2.126185 H_ene -0,923621 -1,232253 -2,126185 H_ene -0,923621 1,232253 -2,126185 Gh (H_ene) 0,923621 1,232253 -2,126185 - 0 1 Х 9,0 9,0 9,0 C_yne 0,000000 0,000000 2,3 C_yne 0,000000 0,000000 1,693240 H_yne 0,000000 0,000000 0,627352 H_yne 0,000000 0,000000 3,963929 } eneyne.update_geometry () для iat в диапазоне (eneyne.natom ()): print "" "{: 4} {: 4} {: 12} {: 8.4f} {: 12.6f} {: 12.6f} {: 12.6f} {: 12.6f}" "". format ( eneyne.  Z (iat), # атомный номер
eneyne.symbol (iat), # символ элемента
eneyne.label (iat), # метка элемента ввода
eneyne.charge (iat), # заряд элемента
eneyne.x (iat), # координата x
eneyne.y (iat), # координата y
энейн.z (iat), # z-координата
eneyne.mass (iat), # масса
)
# 6.0 C C_ENE 6.0000 -0.031900 -1.218981 -3.948079 12.000000
# 6.0 C C_ENE 6.0000 -0.031900 1.304098 -3.948079 12.000000
# 1.0 H H_ENE 1.0000 1.713491 -2.286062 -3.950962 2.014000
# 1.0 H H_ENE 1.0000 -1.777290 -2.286062 -3.950962 1.007825
# 1.0 H H_ENE 1.0000 -1.777290 2.371180 -3.950962 1,007825
# 0,0 H H_ENE 0,0000 1,713491 2,371180 -3,950962 1,007825
# 6.0 C C_YNE 6.0000 -0.031900 0.042559 5.548101 12.000000
# 6.0 C C_YNE 6.0000 -0.031900 0.042559 3.266705 12.000000
# 1.0 H H_YNE 1.0000 -0.
Z (iat), # атомный номер
eneyne.symbol (iat), # символ элемента
eneyne.label (iat), # метка элемента ввода
eneyne.charge (iat), # заряд элемента
eneyne.x (iat), # координата x
eneyne.y (iat), # координата y
энейн.z (iat), # z-координата
eneyne.mass (iat), # масса
)
# 6.0 C C_ENE 6.0000 -0.031900 -1.218981 -3.948079 12.000000
# 6.0 C C_ENE 6.0000 -0.031900 1.304098 -3.948079 12.000000
# 1.0 H H_ENE 1.0000 1.713491 -2.286062 -3.950962 2.014000
# 1.0 H H_ENE 1.0000 -1.777290 -2.286062 -3.950962 1.007825
# 1.0 H H_ENE 1.0000 -1.777290 2.371180 -3.950962 1,007825
# 0,0 H H_ENE 0,0000 1,713491 2,371180 -3,950962 1,007825
# 6.0 C C_YNE 6.0000 -0.031900 0.042559 5.548101 12.000000
# 6.0 C C_YNE 6.0000 -0.031900 0.042559 3.266705 12.000000
# 1.0 H H_YNE 1.0000 -0. 031900 0.042559 1.252468 1.007825
# 1.0 H H_YNE 1.0000 -0.031900 0.042559 7.557685 1.007825
031900 0.042559 1.252468 1.007825
# 1.0 H H_YNE 1.0000 -0.031900 0.042559 7.557685 1.007825
Декартов театр Матрицы и Аватара — Руне Пейтерсен
© Руне Пайтерсен, 2010
И The Matrix , и, совсем недавно, Avatar обладают способностью главного героя (ов) переносить свой разум / сознание в другое (виртуальное) тело.Предпосылка кажется картезианской. Человеческое сознание заперто где-то внутри нашей головы или мозга, но если бы мы смогли «освободить» его от его материального существования, ничто не мешало бы ему овладеть другим телом.
Современная логика — это компьютерная логика — у всех нас одно и то же материальное оборудование, и поэтому наше программное обеспечение (разум) мгновенно совместимо с любым другим телом. Все, что нам нужно для передачи нашего программного обеспечения, — это какой-то интерфейс. В The Matrix это делается путем прямого подключения к еще большему аппаратному обеспечению, тогда как в Avatar все беспроводное (конечно, между двумя фильмами есть 10+ лет, но нельзя не заметить отчетливого «Матрица», похожая на игрушечную игрушку на ПК, в противоположность внешне гладкому опыту Apple Avatar ). В обоих случаях разум «загружается» в другое оборудование, после чего он может свободно войти в другую реальность, где не действуют правила и ограничения «нормального» мира. IT-работник г-н Андерсон становится супер-крутым, уличным готическим супергероем, а солдат-инвалид становится трехметровым синим «воином», который едет на огромном динозавре-индейке и гвоздет (или, скорее, «хвосты») дочь вождя. (Я содрогаюсь при мысли, что солдаты на базах в США, которые удаленно управляют дронами «Хищник» в Афганистане и других местах, могут вообразить себя претерпевающими аналогичные «преобразования», «отправляясь» на задания).
В обоих случаях разум «загружается» в другое оборудование, после чего он может свободно войти в другую реальность, где не действуют правила и ограничения «нормального» мира. IT-работник г-н Андерсон становится супер-крутым, уличным готическим супергероем, а солдат-инвалид становится трехметровым синим «воином», который едет на огромном динозавре-индейке и гвоздет (или, скорее, «хвосты») дочь вождя. (Я содрогаюсь при мысли, что солдаты на базах в США, которые удаленно управляют дронами «Хищник» в Афганистане и других местах, могут вообразить себя претерпевающими аналогичные «преобразования», «отправляясь» на задания).
Хотя кажется, что разум и тело почти не влияют друг на друга, если вообще влияют, в обоих фильмах вам все равно нужно «настоящее» тело. Если ваше «настоящее» тело умирает, вы мертвы. В The Matrix вы умираете, даже если умирает ваше виртуальное тело — по крайней мере, иногда. В Avatar это меньшая проблема; большой синий аватар может выжить без разума в вегетативном, мертвом состоянии — очень удобно. Кроме того, если вам повезет, вы можете навсегда перенести свой разум в большое синее тело, но для этого потребуется много вычислительной мощности, и все синие люди должны приложить усилия, чтобы это работало.Что происходит с первоначальным телом после этого, несколько неясно, но мне нравится представлять, что в истинно тотемистском стиле сердце и печень вырываются из еще теплого тела и ритуально пожираются племенем (обычно, я бы сказал мозг тоже, но в данном конкретном случае можно с уверенностью предположить, что он пуст (?)).
Кроме того, если вам повезет, вы можете навсегда перенести свой разум в большое синее тело, но для этого потребуется много вычислительной мощности, и все синие люди должны приложить усилия, чтобы это работало.Что происходит с первоначальным телом после этого, несколько неясно, но мне нравится представлять, что в истинно тотемистском стиле сердце и печень вырываются из еще теплого тела и ритуально пожираются племенем (обычно, я бы сказал мозг тоже, но в данном конкретном случае можно с уверенностью предположить, что он пуст (?)).
Как правило, мозг регулирует многие жизненно важные функции организма. К ним относятся регулирование температуры, дыхания, сердцебиения, гормонального баланса и т. Д.и т. д. Поскольку тела, оставленные в фильмах, не умирают полностью, мы должны предположить, что переданная часть разума не участвует ни в одной из этих задач. Точно так же новое тело «заботится» о сенсорном вводе, что, по-видимому, означает, что любой мозг устроен совершенно одинаково, когда дело доходит до, например, зрительная кора независимо от того, какие у вас глаза (прощайте, влияние окружающей среды — и здравый смысл), или разум просто оседает на водительском месте нового мозга и позволяет всей сенсорной информации поступать к нему « извне » (привет проблема гомункула). В любом случае текущая индивидуальная нейронная проводка мозга (которая начинается, как только мозг начинает развиваться и является более индивидуальной и сложной, чем отпечаток пальца размером с луну), кажется, играет незначительную роль или вообще не играет никакой роли, что является хорошо, потому что это создало бы проблему — как бы вы перенесли с собой новые воспоминания или недавно приобретенные навыки из одного тела в другое, если бы воспоминания и недавно приобретенные навыки были структурами мозга? Фактически, можно с уверенностью сказать, что единственные аспекты разума, которые передаются, это: личность (что бы это ни было, когда оно было отделено от телесного опыта и индивидуально запрограммированной нейронной сети), память (что бы это ни было, когда оно отделено от телесный опыт и индивидуально запрограммированная нейронная сеть) и эмоции (что бы это ни было, когда оно отделено от телесного опыта и индивидуально запрограммированной нейронной сети).
В любом случае текущая индивидуальная нейронная проводка мозга (которая начинается, как только мозг начинает развиваться и является более индивидуальной и сложной, чем отпечаток пальца размером с луну), кажется, играет незначительную роль или вообще не играет никакой роли, что является хорошо, потому что это создало бы проблему — как бы вы перенесли с собой новые воспоминания или недавно приобретенные навыки из одного тела в другое, если бы воспоминания и недавно приобретенные навыки были структурами мозга? Фактически, можно с уверенностью сказать, что единственные аспекты разума, которые передаются, это: личность (что бы это ни было, когда оно было отделено от телесного опыта и индивидуально запрограммированной нейронной сети), память (что бы это ни было, когда оно отделено от телесный опыт и индивидуально запрограммированная нейронная сеть) и эмоции (что бы это ни было, когда оно отделено от телесного опыта и индивидуально запрограммированной нейронной сети).
Все равно главное, что работает. По-видимому, нам говорят, что это всего лишь вопрос правильной технологии, прежде чем мы все сможем стать героями в нашей собственной жизни — быть тем, кем мы действительно должны были быть — просто загрузив наш «разум» в другое тело. Это к счастью, потому что тогда нам не нужно беспокоиться о том, чтобы быть «теми, кем мы действительно должны были быть» в повседневной жизни, все, что нам нужно сделать, это дождаться появления нужной технологии, и тогда мы сможем превратиться в борцы за свободу на далеких планетах или в мире, где доминируют машины.Наконец-то мы можем быть такими же храбрыми и смелыми, какими мы на самом деле являемся. Мы будем бороться с угнетением, освободить некоторых людей и в конце концов получить девушку. Другими словами, мы наконец-то можем делать все то, что нам суждено было сделать, но вы не можете делать в реальном мире … потому что вам не разрешено, или нигде нет угнетенных людей, нет несправедливости и нет девушек.
По-видимому, нам говорят, что это всего лишь вопрос правильной технологии, прежде чем мы все сможем стать героями в нашей собственной жизни — быть тем, кем мы действительно должны были быть — просто загрузив наш «разум» в другое тело. Это к счастью, потому что тогда нам не нужно беспокоиться о том, чтобы быть «теми, кем мы действительно должны были быть» в повседневной жизни, все, что нам нужно сделать, это дождаться появления нужной технологии, и тогда мы сможем превратиться в борцы за свободу на далеких планетах или в мире, где доминируют машины.Наконец-то мы можем быть такими же храбрыми и смелыми, какими мы на самом деле являемся. Мы будем бороться с угнетением, освободить некоторых людей и в конце концов получить девушку. Другими словами, мы наконец-то можем делать все то, что нам суждено было сделать, но вы не можете делать в реальном мире … потому что вам не разрешено, или нигде нет угнетенных людей, нет несправедливости и нет девушек.
Но что, если технология не будет разработана при нашей жизни?!? К счастью, фильмы, кажется, тоже имеют дело с этой возможностью. Это немного сложно, но тем не менее.Утверждая, что разум (или, по крайней мере, те мифологические 10%, о которых мы заботимся) — это нечто отдельное от тела, кажется правдоподобным, что он может выжить и после того, как мы умрем, — поскольку тело действительно не нужно после все. А затем, возможно, после смерти мы сможем отправиться в то место, где мы наконец сможем быть «теми, кем мы действительно должны были быть», но не смогли быть в нашей прежней жизни (по причинам, упомянутым выше). Это может показаться смутно знакомым, и я могу только предположить, что это благородное намерение создателей фильма.Дать нам знать, что это нормально, если мы не герои или даже главные герои своей жизни, потому что в Матрице / Пандоре / Загробной жизни мы будем ими. Таким образом, даже если может показаться, что фильмы показывают нам что-то новое, на самом деле они рассказывают нам что-то старое. Они дают нам взгляд на мир 17-го века, одетый в эффекты 21-го века.
Это немного сложно, но тем не менее.Утверждая, что разум (или, по крайней мере, те мифологические 10%, о которых мы заботимся) — это нечто отдельное от тела, кажется правдоподобным, что он может выжить и после того, как мы умрем, — поскольку тело действительно не нужно после все. А затем, возможно, после смерти мы сможем отправиться в то место, где мы наконец сможем быть «теми, кем мы действительно должны были быть», но не смогли быть в нашей прежней жизни (по причинам, упомянутым выше). Это может показаться смутно знакомым, и я могу только предположить, что это благородное намерение создателей фильма.Дать нам знать, что это нормально, если мы не герои или даже главные герои своей жизни, потому что в Матрице / Пандоре / Загробной жизни мы будем ими. Таким образом, даже если может показаться, что фильмы показывают нам что-то новое, на самом деле они рассказывают нам что-то старое. Они дают нам взгляд на мир 17-го века, одетый в эффекты 21-го века.
Как превратить 2D-изображение в 3D-пространство?
Две матрицы, которые мы собираемся увидеть, позволяют нам перейти от декартовой системы координат к проекционной системе координат и наоборот, соответственно H и H ’. Обратите внимание, что H ’ не является обратной матрицей H .
Обратите внимание, что H ’ не является обратной матрицей H .
Чтобы объяснить координаты проекции, я для простоты проведу аналогию в 2D. Представьте себе экран размером X , Y , который довольно легко изобразить. Тогда у нас есть (X, Y, W) , где W — это расстояние экран-проектор . Итак, мы находимся в двумерном пространстве в проективных (или однородных) координатах.
Теперь, когда мы находимся в этом проекционном пространстве, мы можем переместить проектор вперед на или назад на от экрана на расстояние ΔW .Если мы переместим его назад, то проецируемое изображение будет проецироваться за его пределы. И наоборот, если приблизить проектор к экрану, размер изображения на экране уменьшается.
Невозможно (или сложно) представить это проективное пространство, связанное с трехмерным декартовым пространством, но принцип остается тем же. У нас будет (X, Y, Z, W) .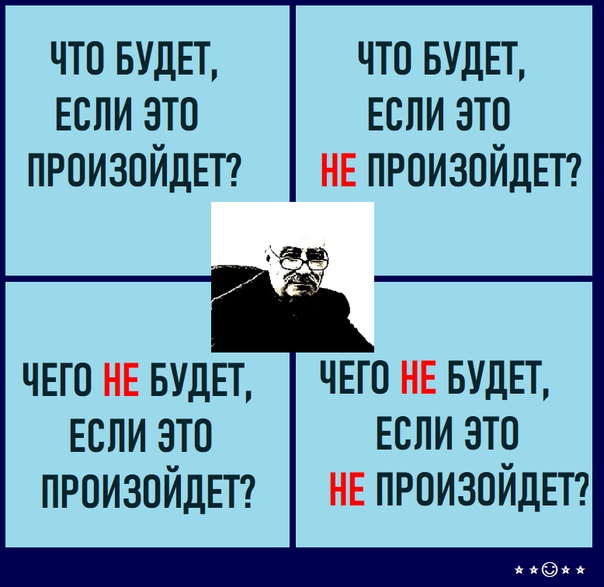
В следующих сценариях мы применим эти матрицы преобразования, рассматривая углы в градусов (от 0 ° до 360 °) и измерения в пикселей .
На данный момент мы не определили матрицы преобразования. Мы определим их позже. Мы заменим их на матрицу Identity . Эта матрица не изменяет изображение, это как умножение числа на 1 .
Давайте вернемся к нашим матрицам для перехода от декартовых координат к проективным координатам и наоборот. На данный момент матрица M является единичной матрицей.
Здесь h и w — это высота и ширина изображения, которое нужно обработать.
Если в нашем уравнении появляются h и w , это означает, что центрирует отметку в центре изображения. Действительно, на изображении точка отсчета находится в верхнем левом углу изображения (координаты (0, 0) ).
Также мы можем видеть появление переменной f , которая соответствует фокусному расстоянию нашего проектора на диаграмме, которую мы видели ранее.
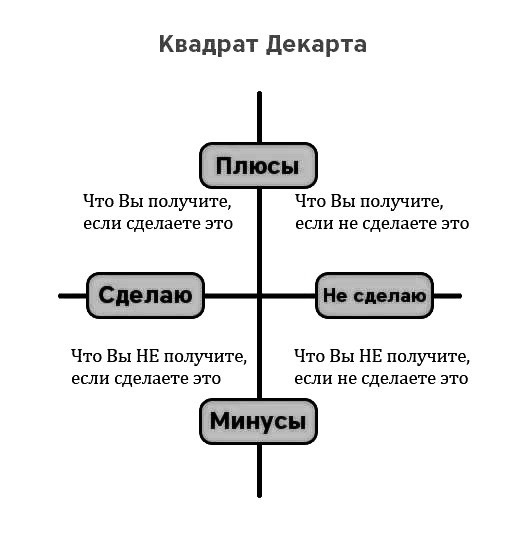 Этот патч можно применять
# где угодно в спецификации координат, если оно меньше
# ссылки на атомы, как обычно для Z-матриц
C 2 rCC 3 aCCC 1 dCCCN
H 7 rCh2 2 aHCC1 3 dHCCC1
H 7 rCh3 2 aHCC2 3 dHCCC2
H 7 rCh4 2 aHCC3 3 dHCCC3
H 0,221781602033 1,772570540211 0,286988509018
Н -1.833601608592 0.108401996052 1.481873213172
В -1.925572581453 1.640882152784 0.986471814808 аССК = 108,0
rCC = 1,4
dCCCN = 120
rCh2 = 1,08
rCh3 = 1,08
rCh4 = 1,08
аНСС1 = 109,0
аНСС2 = 109,0
аНСС3 = 109,0
dHCCC1 = 0,0
dHCCC2 = 120,0
dHCCC3 = 240,0
}
Этот патч можно применять
# где угодно в спецификации координат, если оно меньше
# ссылки на атомы, как обычно для Z-матриц
C 2 rCC 3 aCCC 1 dCCCN
H 7 rCh2 2 aHCC1 3 dHCCC1
H 7 rCh3 2 aHCC2 3 dHCCC2
H 7 rCh4 2 aHCC3 3 dHCCC3
H 0,221781602033 1,772570540211 0,286988509018
Н -1.833601608592 0.108401996052 1.481873213172
В -1.925572581453 1.640882152784 0.986471814808 аССК = 108,0
rCC = 1,4
dCCCN = 120
rCh2 = 1,08
rCh3 = 1,08
rCh4 = 1,08
аНСС1 = 109,0
аНСС2 = 109,0
аНСС3 = 109,0
dHCCC1 = 0,0
dHCCC2 = 120,0
dHCCC3 = 240,0
} 