Метод статистического вывода в психологии: 2) Методы статистического вывода

2) Методы статистического вывода

Рассмотрим вторую большую группу количественных методов анализа, на основе которых делается статистический вывод. В этом случае стоит задача перехода от отдельной выборки к характеристикам (параметрам) генеральной совокупности, то есть всего класса объектов в целом. Дело в том, что исследователь редко имеет возможность изучать всех представителей какой-то группы или социальной категории. Можно, например, обследовать все многодетные семьи, проживающие в данном микрорайоне, но тогда выводы в полной мере будут относиться лишь к этой конкретной группе людей. Насколько они справедливы для многодетных семей всего города или области? Чтобы ответить на этот вопрос, нужно знать, насколько типична или специфична обследованная группа. Если она типична, то сходные проблемы выявятся и у других многодетных семей. Если группа очень специфична, то мы не имеем права обобщать полученные данные. На языке статистики это значит, что наша выборка принадлежит к другой генеральной совокупности.

Опять мы сталкиваемся с задачей сравнения характеристик выборки и генеральной совокупности, с необходимостью суждения об их тождестве или различии.

В реальной практике исследования вопрос чаще всего ставится несколько иначе, но логически он относится к тому же классу. Требуется сравнить две группы (выборки) и решить, насколько значимо они различаются между собой. Любой эксперимент предполагает оценку эффекта изучаемого воздействия. Исследователь в этом случае стремится показать, что экспериментальная группа существенно отличается в интересующем его отношении от контрольной группы. Оценивая эффективность образовательных программ, лечебных и оздоровительных мероприятий, мы смотрим, насколько существенными оказываются позитивные сдвиги. И что называть сдвигом? Если больной выздоровел, то это явный качественный сдвиг. Если ему стало легче, его меньше беспокоят боли, то это некоторый количественный сдвиг. Но можно ли говорить о переходе из одного состояния в другое? Для этого нам нужны критерии тождества или различия двух состояний.

Статистика предлагает определенные формальные правила, позволяющие делать такого рода выводы.

Общая логика рассуждений такова. У нас есть два множества объектов. Если различие между ними по какому-то параметру настолько очевидное, что эти два множества не пересекаются, можно с уверенностью сказать, что это два разных класса объектов. Например, если минимальное значение дохода в одной группе населения превышает максимальное значение дохода в другой группе, то мы вправе утверждать, что группы различаются по своему материальному положению. Но это случай весьма тривиальный. Никому не придет в голову проводить исследования, чтобы доказать, что слон больше муравья. Это очевидно. Наука имеет дело с нетривиальными задачами, то есть с такими ситуациями, где на основании имеющихся знаний мы выдвигаем какие-то более или менее правдоподобные гипотезы, которые еще нуждаются в проверке и в доказательстве. Обычный случай, с которым имеет дело ученый, – это частично пересекающиеся множества (частично перекрывающиеся распределения).

Вот тут и встает проблема различения и отождествления.

Проблема осложняется тем, что, кроме нечеткости категорий (математики в этом случае говорят о размытых множествах), нужно учитывать возможность всякого рода ошибок. Ошибки измерений связаны с точностью тех инструментов, которые мы используем. Никакой инструмент не дает абсолютной точности измерений. Надежность тех методов сбора информации, которыми пользуются исследователи в социальных науках, далеко уступает надежности физических приборов. Кроме того, нужно учитывать возможную ошибку выборки. Так как для исследования берутся только некоторые экземпляры, у нас нет никакой гарантии, что они являются типичными представителями популяции в целом. Рассмотренные нами ранее способы корректного построения выборки направлены на устранение систематической ошибки, но случайные ошибки полностью исключить невозможно. Статистика ставит перед собой задачу: оценить степень надежности получаемых данных и степень надежности тех выводов, которые делаются на их основе.

Для этой цели используется аппарат теории вероятностей.

Нетрудно доказать, что ошибка выборки зависит от двух моментов: от размера выборки и от степени вариации признака, который нас интересует. Чем больше выборка, тем меньше вероятность того, что в нее попадут индивиды с крайними значениями исследуемой переменной. С другой стороны, чем меньше степень вариации признака, тем в целом ближе будет каждое значение к истинному среднему. Размер выборки нам известен, а степень вариации признака можно примерно оценить по степени разброса данных. Таким образом, зная размер выборки и получив меру рассеяния наблюдений, нетрудно вывести показатель, который называется стандартная ошибка среднего. Он дает нам интервал, в котором должна лежать истинная средняя популяции.

Описанная процедура основана на том факте, что ошибки выборки и ошибки измерений вообще подчиняются нормальному закону, поскольку они обусловлены множеством случайных факторов. При этом совершенно не обязательно, чтобы само распределение данных имело нормальный вид.

Представим себе, что мы изучаем разные случайные выборки из одной генеральной совокупности. Оценки среднего, получаемые в каждом случае, будут несколько различаться между собой, но в целом они будут группироваться вокруг истинного значения. Если построить распределение этих оценок, то оно окажется нормальным. В центре его будет лежать среднее по генеральной совокупности, а стандартное отклонение будет равно стандартной ошибке среднего. Но последний показатель, как мы видели, можно вывести и на основании одной выборки, вычисляя по формуле: «Стандартная ошибка = стандартное отклонение, деленное на корень квадратный из числа наблюдений». Теперь, зная свойства нормального распределения, можно указать интервал, в котором должно находиться истинное среднее. Выше, рассматривая свойства нормального распределения, мы отмечали, что в диапазоне двух стандартных отклонений в обе стороны от среднего сосредоточено примерно 95 % всех случаев. Значит, вероятность получить значение, выходящее за эти пределы, не превышает 5 %, то есть такие ошибки будут встречаться не чаще, чем один раз из 20 случаев. С вероятностью 0,95 можно утверждать, что истинное значение лежит в указанных границах, которые задают доверительный интервал.

Итак, поскольку какая-то вероятность ошибки всегда присутствует, мы вводим количественную меру надежности наших выводов. Все статистические критерии построены по этому принципу. Уровень 95 % принят как соответствующий достаточной надежности суждений. Если мы стремимся к еще большей надеж­ности, то можно взять 99 % уровень. Это означает, что случайная ошибка допускается не чаще, чем в одном случае из ста. Точные доверительные границы для 95 % уровня составляют ±1,96 стандартной ошибки среднего, а для 99 % уровня мы используем коэффициент 2,58. В первом случае вне этого интервала остается не более 5 % возможных значений (по 2,5 % с каждой стороны). Во втором случае – не больше 1 % (по 0,5 % с каждой стороны).

Рассмотрим пример. Допустим, что в некоторой группе безработных из 25 человек средний возраст оказался 32 года. Массовые исследования говорят, что средний возраст для этой категории составляет 40 лет, а стандартное отклонение составляет 6 лет.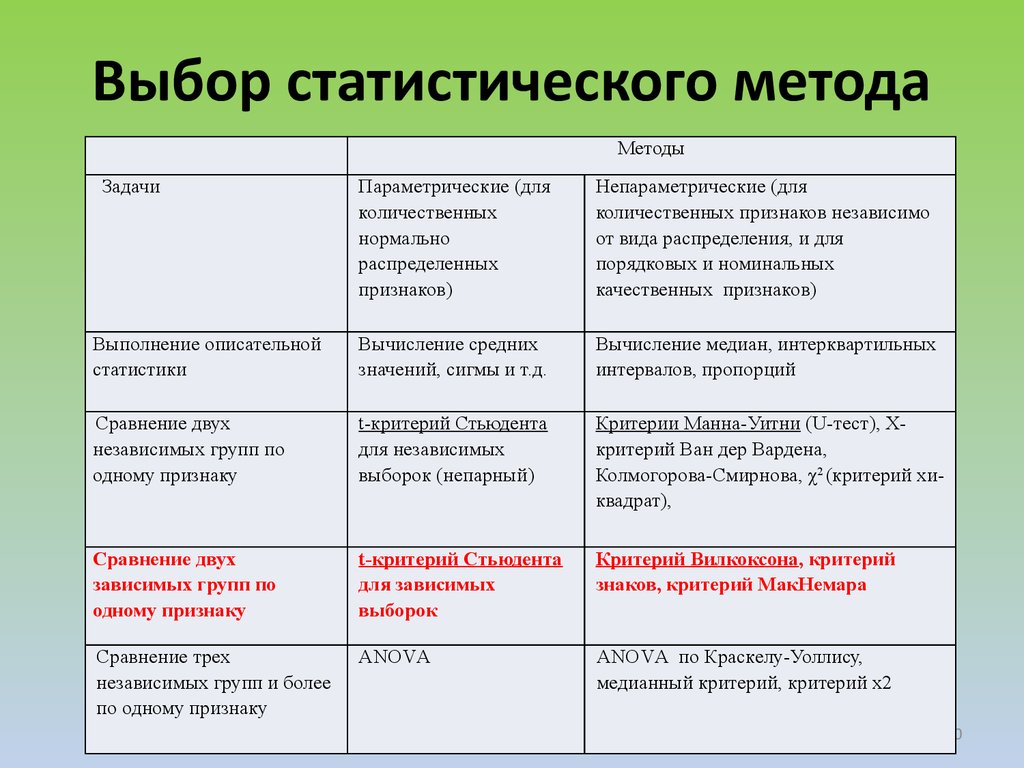 Нас интересует вопрос, типична или нетипична наша выборка. Если это перевести на язык статистики, то мы спрашиваем, можно ли объяснить различие средних ошибкой выборки.

Статистический вывод представляет собой процесс проверки гипотез. Первоначально всегда выдвигается предположение, что наблюдаемые различия носят случайный характер, то есть выборка принадлежит к той же генеральной совокупности. В статистике такое предположение получило название нулевая гипотеза. Итак, мы полагаем для начала, что наша выборка вполне типична. А затем мы спрашиваем: «Какова вероятность получить выборку с таким средним (32 года) из генеральной совокупности, средний возраст которой нам известен (40 лет)?» Мы знаем, что при многократных испытаниях получаемые значения будут распределены нормально, и средняя этого распределения будет равна 40 годам. Стандартную ошибку при условии, что мы будем каждый раз брать по 25 человек, можно рассчитать по известной нам формуле: мы делим 6 (стандартное отклонение) на корень квадратный из 25 и получаем значение 1,2 года (стандартная ошибка среднего).

Затем вычисляется доверительный интервал, который в нашем случае при уровне достоверности в 95 % составит:

40 + 1,96 – 1,2 года = 40 ± 2,35 года (т. е. от 37, 65 до 42, 35).

Значение среднего для нашей выборки (32) лежит вне найденного диапазона. Это может означать, что:

а) либо мы наткнулись на тот чрезвычайно редкий случай, который лежит на самом краю распределения;

б) либо наше предположение, что два средних (по выборке и по генеральной совокупности) не различаются, ошибочно.

Если основываться только на имеющихся данных, то мы имеем основание отклонить нулевую гипотезу, то есть считать, что наша группа какая-то особая. Мы говорим, что различие между средними статистически значимо на уровне р < 0,05. Вероятность ошибки составляет менее 5 %, и поэтому мы с достаточной уверенностью утверждаем, что различие не случайно. Если мы задаем более строгий критерий (99 %), то у нас еще больше оснований отклонить нулевую гипотезу. Мы говорим тогда, что различие статистически высоко значимо. Для социальных исследований 95 % уровень значимости считается вполне приемлемым.

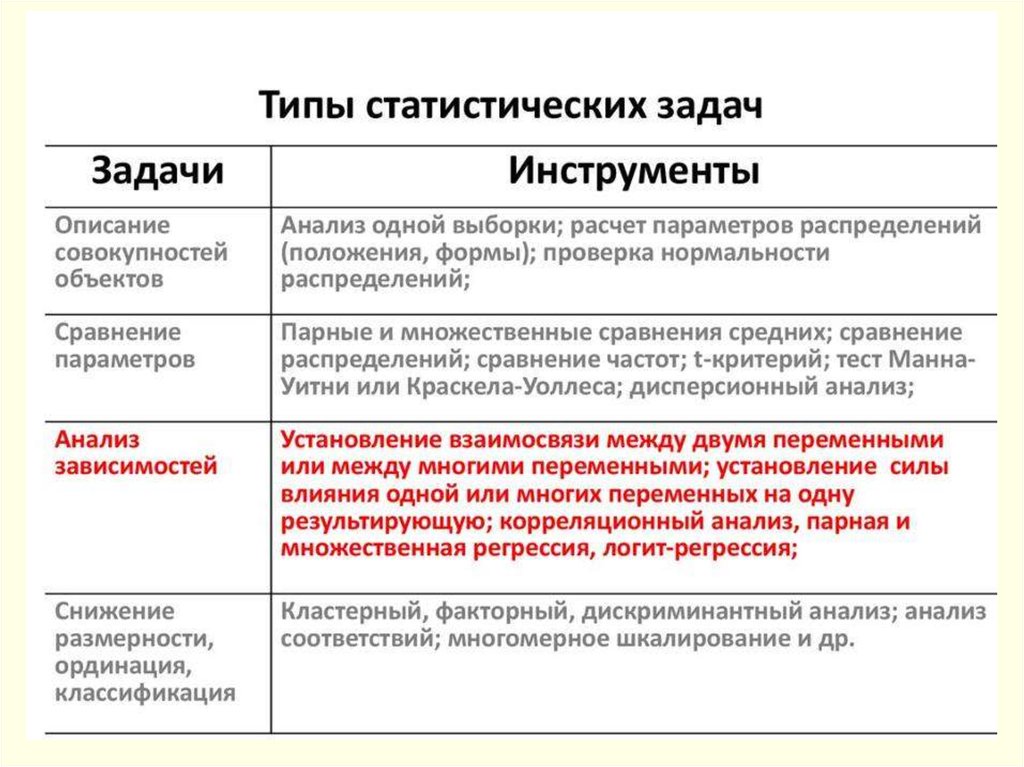
Разобранный пример иллюстрирует случай сравнения эмпирического и теоретического распределения. Аналогичная процедура применяется и тогда, когда требуется оценить различие двух выборок. Мы исходим из допущения, что наблюдаемое различие средних обусловлено случайными факторами (ошибкой выборки и измерения). Другими словами, мы предполагаем, что обе выборки принадлежат к одной генеральной совокупности, параметры которой нам неизвестны. Затем мы оцениваем различие средних с учетом наблюдаемого рассеяния данных в каждой из выборок. Критические значения задаются с учетом выбранного уровня значимости. Если заданная величина оказывается превышенной, мы отвергаем нулевую гипотезу и считаем, что наблюдаемые различия не случайны.

Мы разобрали принципы проверки статистических гипотез. Существуют разные статистические критерии, разработанные для разных типов данных. Некоторые из них, так называемые параметрические критерии, применимы только к данным, полученным с помощью интервальных шкал. Название отражает тот момент, что в основе процедуры оценки лежит предположение о характере распределения данных. Если эти условия не выполняются, то выводы оказываются сомнительными. К наиболее известным критериям этого типа относится критерий Стьюдента, применяемый для оценки различия средних. Но разработан также целый ряд статистических процедур, которые не привязаны к какому-то определенному распределению. Эти критерии, которые называются непараметрическими, особенно удобны для анализа данных, с которыми обычно имеют дело социальные науки. Примером может служить критерий «хи-квадрат», который основан на сравнении частот. Кстати, этот же метод используется для оценки связи между качественными признаками. Выбор подходящего критерия – задача весьма непростая. Здесь следует обратиться к помощи специалиста по математической статистике.

Нужно помнить, что грамотное применение статистики требует от исследователя специальной подготовки, но это касается и приемов качественного анализа, и методов сбора данных. По методам обработки социальной информации имеется обширная литература – от элементарных учебников до серьезных руководств.

Что такое описательная статистика — СибАК

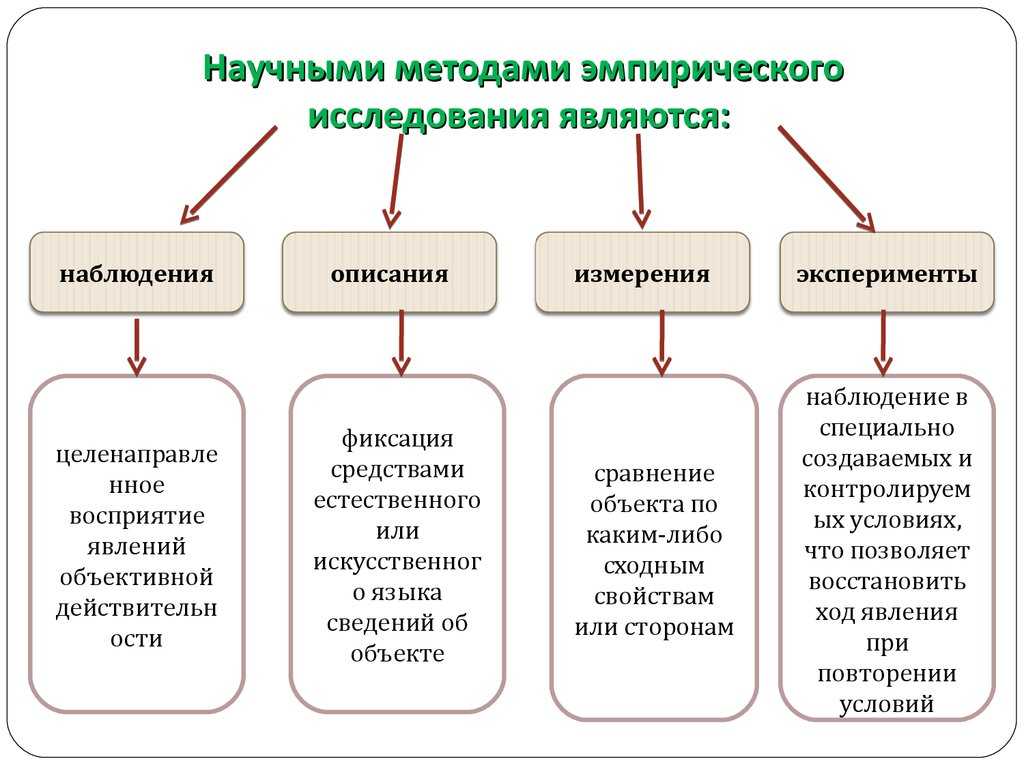
Методы описательной статистики

21.02.2020

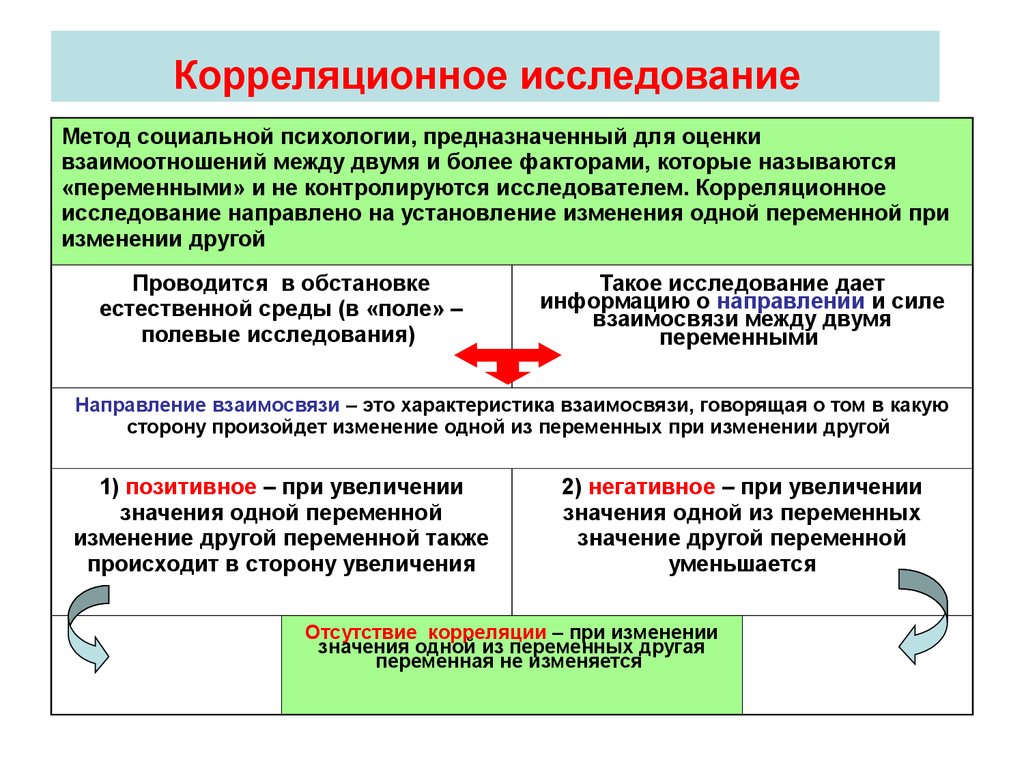
Исследования

Автор: Редакция СибАК

Практически каждый исследователь сталкивается рано или поздно в своей работе с необходимостью обработки и дальнейшего предоставления статистических данных. Причем это касается самых разных отраслей науки – от технических и медицинских до социологических и культурологических.

Обусловлена такая распространенность тем, что статистические методы помогают получить и обосновать определенные суждения об объектах, субъектах, группах людей и прочем, что обладает определенной внутренней неоднородностью.

Вы можете заказать услугу срочной публикации научных статей в научных журналах. Специалисты издательства СибАК знают, как выполнить работу в сжатые сроки.

Что такое описательная статистика

Те, кто впервые в своей работе сталкивается с обработкой и описанием данных, не всегда четко представляют, в какой форме их корректно отображать и обрабатывать для того, чтобы в дальнейшем подвергнуть статистическому выводу.

Поэтому нужно четко представлять, что такое описательная статистика. Она еще носит название дескриптивной и занимается анализом и обработкой эмпирических данных с проведением необходимой систематизации. Описательная статистика – это сжатая и концентрированная характеристика изучаемого явления, представленная в виде графиков, таблиц, схем и числовых выражений.

Вот что входит в описательную статистику в качестве основных показателей:

• переменная, которая не является постоянным. Ее можно не только измерять, но и подвергать изменениям в ходе определенных манипуляций;
• экстремумы, или так называемые максимумы и минимумы значений самой переменной;
• под вариационными рядами понимают все количественные признаки, которые имеются у каждой единицы статистического наблюдения;
• среднее – представляется средним арифметическим или выборочным. Здесь есть несколько параметров, таких как гармоническое, геометрическое, арифметическое и квадратическое. Все они нужны для того, чтобы охарактеризовать центр распределения;
• мода представляет собой наиболее часто встречающееся значение в выборке. Правда, она может отражать также и среднее значение класса, обладающего наибольшей частотой;
• медиана – это среднее значение чаще всего встречающихся значений выборки;
• дисперсия – позволяет оценить отклонения в определенном числе наблюдений. Этот параметр относится к показателям рассеяния вариант.

Помимо этого, для осуществления методов описательной статистики используют еще такие показатели, как квартили, асимметрию, статистические моменты, эксцессы, гипотезы, значимости. Каждый из них играет существенную роль для корректного отображения получаемых данных.

Совокупность выше представленных показателей помогает при визуальном представлении данных осуществить:

• фиксацию их относительно осей, придав тем самым вес в числовом отражении;
• отобразить, насколько они разбросаны относительно своего центра;
• показать асимметричность распределения около центрального положения;
• вывести закон распределения данных при помощи гистограммы, таблицы частот или функции.

Как сделать описательную статистику

При выполнении определенного вида работ и решении задач придерживаются следующего порядка.

1. Собирают все необходимые исходные данные. При этом учитывают размер выборки. Чтобы получить достоверные данные, минимальное число не может быть меньше 1000. Чем оно будет больше, тем точнее получится итоговый результат.
2. На втором этапе строят вариационный ряд. Все полученные данные упорядочивают по возрастанию. Чтобы это было удобнее выполнить, находят минимальный и максимальный элементы, а затем относительно них переписывают его в нужной последовательности.
3. В некоторых случаях для упрощения процедуры обработки допускается вычитание из каждого элемента ряда минимального значения. Таким образом, работа дальше ведется не с конкретными размерами, а только с их отклонениями.
4. На следующем этапе проводят группировку данных. Для этого их разбивают на R интервалов, число которых соотносят с количеством наблюдений.
5. Затем определяют частости и эмпирические плотности вероятностей (частость используется для того, чтобы заменить частоты при составлении вариационных рядов).
6. После этих обработок собранной информации необходимо построить полигон. Но для этого первоначально определяют масштаб по осям.
7. Когда этот этап выполнен, строят гистограмму и эмпирическую функцию распределения.
8. Используя данные из гистограммы рассчитывают параметры распределения.
9. И на финальном этапе оформляют результат, который сводят в таблицу, схему, гистограмму, график или прочее.

Обработку статистических параметров методом описательной статистики необходимо проводить на высшем уровне. В противном случае могут пострадать итоговые выводы и результаты научной работы.

Важность корректного представления данных

Статистическое отображение данных важно в любой научной работе. А для публикаций в журналах, индексируемых наукометрическими базами Web of Science и Scopus, нужно особо тщательно относиться к качеству подаваемого материала.

Можно самому разбираться во всех тонкостях и сложных формулах, которые нужно применять. Но, чтобы облегчить и ускорить процесс статистической обработки в исследовании, лучше обратиться к специалистам, которые доступно объяснят даже самые сложные моменты.

Автор: СибАК

Читайте также

Гранты на научные исследования для молодых ученых

Методы выдвижения, постановки и проверки научной гипотезы

Основные методы научного исследования

Форма обратной связи о взаимодействии с сайтом

Укажите Ваше имя *

Адрес Вашей электронной почты *

Оставьте свой комментарий, если у вас возникли проблемы при работе с сайтом

Согласие *

Я согласен (-на) с условиями Публичной Оферты и даю свое Согласие на обработку персональных данных

Статистический вывод — определение, типы, процедура и пример

Статистика — это раздел математики, который занимается сбором, анализом, интерпретацией и представлением числовых данных. Другими словами, это определяется как сбор количественных данных. Основная цель статистики состоит в том, чтобы сделать точный вывод, используя ограниченную выборку о большей совокупности.

Типы статистики

Статистика может быть разделена на две категории. Два разных типа статистики:

• Описательная статистика
• Логическая статистика

В статистике описательная статистика описывает данные, тогда как статистика логического вывода помогает делать прогнозы на основе данных. В логической статистике данные берутся из выборки и позволяют обобщить совокупность. В общем, умозаключение означает «угадывать», то есть делать выводы о чем-либо. Итак, статистический вывод означает вывод о населении. Чтобы сделать вывод о населении, он использует различные методы статистического анализа. В этой статье подробно объясняется один из типов статистики, называемой статистикой вывода. Теперь вы узнаете правильное определение статистического вывода, типов, решений и примеров.

Определение статистического вывода

Статистический вывод — это процесс анализа результатов и выводов на основе данных, подверженных случайным колебаниям. Ее также называют логической статистикой. Проверка гипотез и доверительные интервалы являются приложениями статистического вывода. Статистический вывод — это метод принятия решений о параметрах совокупности на основе случайной выборки. Это помогает оценить взаимосвязь между зависимой и независимой переменными. Цель статистического вывода — оценить неопределенность или вариацию от выборки к выборке. Это позволяет нам предоставить вероятный диапазон значений для истинных значений чего-либо в совокупности. Компоненты, используемые для статистического вывода:

• Размер образца
• Изменчивость в образце
• Размер наблюдаемых различий

Типы статистического вывода

Существуют различные типы статистических выводов, которые широко используются для получения выводов. Они:

• Проверка гипотезы с одним образцом
• Доверительный интервал
• Корреляция Пирсона
• Двумерная регрессия
• Многомерная регрессия
• Статистика хи-квадрат и таблица непредвиденных обстоятельств
• Дисперсионный анализ или Т-тест

Процедура статистического вывода

Процедура, используемая в выводной статистике:

• Начните с теории
• Создать исследовательскую гипотезу
• Операционализация переменных
• Распознать популяцию, к которой следует применить результаты исследования
• Сформулируйте нулевую гипотезу для этой совокупности
• Накопить выборку из населения и продолжить исследование
• Провести статистические тесты, чтобы увидеть, достаточно ли отличаются свойства собранной выборки от того, что можно было бы ожидать при нулевой гипотезе, чтобы можно было отвергнуть нулевую гипотезу

Решение для статистического вывода

Решения для статистического вывода позволяют эффективно использовать статистические данные, относящиеся к группам людей или испытаниям. Он касается всех персонажей, включая сбор, исследование и анализ данных, а также организацию собранных данных. С помощью решения статистического вывода люди могут приобретать знания после начала своей работы в различных областях. Некоторые факты решения статистического вывода:

• Обычно предполагается, что наблюдаемая выборка представляет собой независимые наблюдения из популяции типа Пуассона или нормального
• Решение статистического вывода используется для оценки параметра(ов) ожидаемой модели, такой как нормальное среднее или биномиальная пропорция

Важность статистического вывода

Инференциальная статистика важна для правильного изучения данных. Чтобы сделать точный вывод, важен правильный анализ данных для интерпретации результатов исследования. Он в основном используется в предсказании будущего для различных наблюдений в разных областях. Это помогает нам сделать вывод о данных. Статистический вывод имеет широкий спектр применения в различных областях, таких как:

• Бизнес-анализ
• Искусственный интеллект
• Финансовый анализ
• Обнаружение мошенничества
• Машинное обучение
• Рынок акций
• Фармацевтический сектор

Примеры статистического вывода

Ниже приведен пример статистического вывода.

Вопрос: Из перетасованной колоды вытягивается карта. Это испытание повторяется 400 раз, и масти приведены ниже:

Костюм	Лопата	Булавы	Сердца	Алмазы
Количество розыгрышей	90	100	120	90

Пока карта пробуется наугад, какова вероятность получить

1. Алмазные карты
2. Черные карты
3. Кроме лопаты

Решение:

По решению статистического вывода,

Общее количество событий = 400

т. е. 90+100+120+90=400

(1) Вероятность получения алмазных карт:

Количество попыток, в которых вытягивается алмазная карта = 90

Следовательно, P(алмазная карта) = 90/400 = 0,225

(2) Вероятность получения черных карт:

Количество попыток, в которых выпала черная карта = 90+100 =190

Следовательно, P(черная карта) = 190/400 = 0,475

(3) Кроме лопаты

Количество попыток, отличных от лопаты, появилось = 90+100+120 =310

Следовательно, P(кроме лопаты) = 310/400 = 0,775

Следите за обновлениями BYJU’S — обучающего приложения, чтобы узнать больше о связанных с математикой понятиях, и загрузите приложение, чтобы получить больше персонализированных видео.

4 Идеи статистического вывода

Жаргон

• Хотя это и не концепция, существует важный жаргон, с которым вам необходимо ознакомиться, чтобы изучить статистический вывод. Двумя ключевыми терминами являются точечные оценки и параметры генеральной совокупности. Точечная оценка – это статистика, которая рассчитывается на основе данных выборки и служит в качестве наилучшего предположения о неизвестном параметре совокупности. Например, нас может заинтересовать средняя концентрация сперматозоидов в популяции мужчин с бесплодием. В этом примере среднее значение генеральной совокупности является параметром генеральной совокупности, а среднее значение выборки является точечной оценкой, которая является нашим лучшим предположением среднего значения генеральной совокупности. Параметры совокупности обычно неизвестны, поскольку мы редко измеряем всю совокупность.

 

  Что такое статистический вывод?

• Статистическая практика в целом делится на две категории (1) описательная и (2) выводная. Когда мы просто описываем или изучаем наблюдаемые выборочные данные, мы делаем описательную статистику (см. тему 1). Однако нам часто также интересно понять то, что не наблюдается в более широкой популяции, это может быть, например, среднее кровяное давление среди беременных женщин, или истинное влияние препарата на частоту наступления беременности, или новое лечение. работать лучше или хуже, чем стандартное лечение. В таких ситуациях мы должны признать, что почти всегда мы наблюдаем только один образец или проводим один эксперимент. Если бы мы взяли другой образец или провели еще один эксперимент, то результат почти наверняка изменился бы. Это означает, что в нашем результате есть неопределенность, если мы взяли другой образец или провели другой эксперимент и основывали наш вывод исключительно на данных наблюдаемого образца, мы можем даже сделать другой вывод!
• Цель статистического вывода – оценить эту выборку по вариации или неопределенности выборки. Понимание того, насколько наши результаты могут отличаться, если мы проведем исследование еще раз, или насколько неопределенными будут наши результаты, позволяет нам учитывать эту неопределенность, делая выводы. Это позволяет нам предоставить правдоподобный диапазон значений для истинного значения чего-либо в популяции, например среднего значения или размера эффекта, а также позволяет нам делать заявления о том, предоставляет ли наше исследование доказательства для отклонения гипотезы.

 

Оценка неопределенности:

• Почти все статистические методы, с которыми вы столкнетесь, основаны на том, что называется выборочным распределением. Это совершенно абстрактное понятие. Это теоретическое распределение выборочной статистики, такой как среднее значение выборки, по бесконечным независимым случайным выборкам. Обычно мы проводим только один эксперимент или одно исследование и, конечно же, не повторяем исследование столько раз, чтобы мы могли эмпирически наблюдать распределение выборки. Таким образом, это теоретическое понятие. Однако мы можем оценить, как выглядит выборочное распределение для нашей выборочной статистики или интересующей точечной оценки, основываясь только на одной выборке, одном эксперименте или одном исследовании. Разброс выборочного распределения фиксируется его стандартным отклонением точно так же, как разброс выборочного распределения фиксируется стандартным отклонением. Не путайте распределение выборки и распределение выборки. Одно из них — это распределение отдельных наблюдений, которые мы наблюдаем или измеряем, а другое — теоретическое распределение выборочной статистики (например, среднего), которую мы не наблюдаем . Чтобы не путаться между стандартным отклонением выборочного распределения и стандартным отклонением выборочного распределения, мы называем стандартное отклонение выборочного распределения стандартной ошибкой. Это полезно, потому что стандартное отклонение распределения выборки фиксирует ошибку из-за выборки, таким образом, это мера точности точечных оценок или, другими словами, мера неопределенности нашей оценки. Поскольку мы часто хотим сделать выводы о чем-то в популяции, основываясь только на одном исследовании, понимание того, как наша выборочная статистика может варьироваться от выборки к выборке, также очень полезно. Стандартная ошибка позволяет нам попытаться ответить на такие вопросы, как: каков правдоподобный диапазон значений среднего значения в этой совокупности с учетом среднего значения, которое я наблюдал в этой конкретной выборке? И какова вероятность увидеть такую ​​большую разницу в средствах между этими двумя группами лечения, как я наблюдал, просто из-за случайности? Таким образом, стандартная ошибка является неотъемлемой частью всех статистических выводов, она используется для всех проверок гипотез и доверительных интервалов, с которыми вы, вероятно, когда-либо столкнетесь.

 

  Доверительные интервалы:

• Доверительные интервалы рассчитываются на основе случайной выборки, поэтому они также являются случайными. Долгосрочное поведение 95% доверительного интервала таково, что мы ожидаем, что 95% доверительных интервалов, оцененных по повторной независимой выборке, будут содержать истинный параметр совокупности. Параметр совокупности (например, среднее значение совокупности) не является случайным, он фиксированная (но неизвестная), а точечная оценка параметра (например, выборочное среднее) является случайной (но наблюдаемой). А 95% доверительный интервал определяется средним значением плюс или минус 2 стандартные ошибки. Если оценка, вероятно, находится в пределах двух стандартных ошибок параметра, то параметр, вероятно, находится в пределах двух стандартных ошибок оценки. Это основа, на которой лежит правильная интерпретация и понимание доверительного интервала.

• Таким образом, можно интерпретировать 95% доверительный интервал как «диапазон правдоподобных значений для интересующего нас параметра» или «мы 95 % уверены, что истинное значение находится между этими пределами». Неправильно говорить «вероятность 95 %, что истинное значение совокупности находится между этими пределами». Истинное значение совокупности фиксировано, поэтому оно находится либо в этих пределах, либо или не в этих пределах, нет никакой другой вероятности, кроме 0 (не в CI) или 1 (в CI).Это трудно понять, но если вам это удастся, вы достигнете вехи в понимании статистических идей.

 

  Проверка гипотез:

• Проверка гипотезы задает вопрос: может ли разница, которую мы наблюдали в нашем исследовании, быть случайной?

• Мы никогда не сможем доказать гипотезу, только опровергнем ее или не сможем найти доказательств против нее.

• Статистическая гипотеза называется нулевой гипотезой и обычно формулируется как отсутствие эффекта или разницы, что часто противоречит исследовательской гипотезе, послужившей мотивом исследования.

• Вы можете рассматривать проверку гипотезы как способ количественной оценки доказательств против нулевой гипотезы. Доказательства против нулевой гипотезы оцениваются на основе выборочных данных и выражаются с использованием вероятности (p-значения).

• Значение p – это вероятность получения более экстремального результата, чем наблюдалось, если нулевая гипотеза верна. Все правильные интерпретации p-значения согласуются с этим утверждением.

• Следовательно, если p=0,04, правильно сказать, что «шанс (или вероятность) получения результата, более экстремального, чем тот, который мы наблюдали, составляет 4 %, если нулевая гипотеза верна. Неправильно говорить » вероятность того, что нулевая гипотеза верна, равна 4 %.