Разное

Структура мотивов: Структура мотивации и классификация мотивов

Содержание

Структура мотива.

В структуре мотива выделяют три блока.

Первый блок — потребностный. Если молодой человек осознает свой сексуальный интерес, то он понимает, что надо искать подругу.

Второй блок – блок внутреннего фильтра. Молодой человек смотрит на даму и видит, что у нее красивые ноги – это внешний признак. Парень так же хорошо знает, что она не очень покладиста – это внутренний признак. У него есть декларируемый нравственный контроль, он знает, что с женщинами надо быть вежливым, и на улице лучше не знакомиться. Но у него еще есть не декларируемый нравственный контроль. У него есть определенные притязания и знание, как обаять эту девушку. Он оценивает свои возможности, и свой внешний вид, оценивает свое состояние в данный момент, стоит или нет начинать активно действовать. Это и есть фильтры. Если он прошел эту стадию, и внутренне готов к действию, он начинает действовать, то есть идет дальше.

Третий блок – целевой. Сюда входит определение цели и опредмеченные действия, а так же сам процесс удовлетворения потребности.

Например, подойти и познакомиться, пригласит куда-нибудь и соблазнить.

В структуре мотива всегда работают эти три блока. Иногда бывает, что на втором уровне внутреннего фильтра мотив блокируется. Например, парень узнал, что это жена начальника, и решил не подходить. В этой ситуации он либо переключает свою активность, либо тихо страдает. Для здоровья человека не очень хорошо блокировать свои мотивационные побуждения, необходимо находить способы их реализации. Пример: хотели задать вопрос на лекции, но передумали, потому что показалось, что это вопрос глупый. Утром заболело горло. За все платим.

Характеристики мотивов.

Сила мотива

– она обусловлена физиологическими и психологическими факторами. Есть люди с сильной доминантой, им крайне трудно отклоняться от цели. Сила мотива у многих людей определяется прогнозом, насколько результат достижим.

Устойчивость мотива.

По этим факторам люди и различаются.

Функции мотивов.

Мотивы выполняют три функции:

1. Побуждающая функция, потому что мотив всегда дает энергию.

2. Направляющая функция – потому, что выбирается определенный объект.

3. Регулирующая функция – потому что определяется характер действий, необходимых для достижения цели.

Мотивационные образования и мотивационные черты личности.

В группу так называемых мотивационных образований личности входят мотивационные установки (намерения), влечения, желания и хотения, а также разнообразные интересы.

Мотивационные образования представляют собой результат степени осознания причин возникшего побуждения, а также степени удовлетворения потребности (достижения цели). Поскольку и то и другое может быть разной степени выраженности, постольку и существуют различные мотивационные образования личности.

К мотивационным образованиям относится мотивационная установка. Это своеобразная готовность воспринимать и действовать.

Еще формой мотивационного образования является

желание и величина «хотения». Некоторые авторы используют эти термины как синонимы. Другие разделяют. Желание как осознанное влечение. Хотение имеет большую устремленность.

Интересы – так же форма мотивационного образования. Они побуждают человека к контакту с важными для него явлениями или объектами.

В психологической литературе выделяются так же различные свойства личности, которые так же можно отнести к мотивационным образованиям.

Мотивационные свойства личности.

Полимотивационными свойствами (чертами) личности принято понимать закрепившиеся и предпочитаемые способы формирования мотивов.

Уровень притязаний – определяется степенью достижения субъектом целей, которые он сам ставит перед собой и стремится достичь. Уровень притязаний побуждает активность субъекта, с ним связана его самооценка, он обусловливает не только поведение, но и влияет на формирование характера.

Мотив достижения как устойчивое стремление личности достичь максимально высокого результата, желание выполнить работу хорошо и быстро.

При выраженном мотиве успеха люди, как правило, ориентируются на успех, предпочитая при этом средние по трудности задания, т. е. рискуют весьма расчетливо. Таким людям присущи: большая активность, уверенность в себе, высокая самооценка, женщины более высоко ценят свои деловые качества и стремятся к достижению в значимой для них деятельности, а мужчины больше ценят качества общественного деятеля и стремятся к признанию и соперничеству.

В случае выраженности мотива избегания неудачи люди выбирают либо легкие для себя задания, гарантирующие им успех, либо очень трудные (в этом случае неудача не воспринимается как личный неуспех, а как следствие привходящих и независящих от личности обстоятельств).

Мотив аффиляции (стремление человека быть в обществе других людей). Высокая степень выраженности этого мотива формирует непринужденный, уверенный, открытый стиль общения. Этот мотив положительно связан со стремлением человека к одобрению со стороны окружающих, с желанием самоутверждения.

Такие люди активны и инициативны в общении, отношения с другими строятся на основе взаимного доверия.

Обратной стороной этого мотива является мотив отвержения, т. е. боязнь человека быть отвергнутым другими людьми, вследствие чего у человека преобладают неуверенность, скованность, неловкость.

Мотив власти, понимаемый как потенциал влияния. О доминировании этого мотива говорят тогда, когда человек получает удовлетворение от контроля над другими людьми, от возможности судить, устанавливать нормы и правила поведения.

В основе этого мотива лежит комплекс превосходства, который, по мнению А. Адлера, является врожденным и фундаментальным мотивом человеческой жизни. Впервые это стремление к превосходству начинает осознаваться ребенком на 5-м году жизни, когда начинает формироваться жизненная цель. Будучи неясной и в основном неосознанной в начале жизни, эта цель со временем становится источником мотивации, силой, организующей нашу жизнь и придающей ей смысл.

По мнению А. Адлера превосходство как цель может принимать как деструктивное, так и конструктивное направление. Деструктивное направление характерно для плохо адаптирующихся к обществу людей, что вынуждает их в борьбе за превосходство над другими прибегать к эгоистичному поведению. Хорошо приспосабливающиеся люди проявляют свое превосходство в конструктивном направлении, так, чтобы оно соотносилось с благополучием других людей.

Некоторые исследователи, в частности Р. Мейли, к мотивационным чертам личности относят тревожность, агрессивность и сопротивляемость фрустрации.

Строго говоря, все эти свойства скорее относятся к психодинамическим параметрам индивида, поскольку они определяют динамику психической деятельности.

Мотивация личности

В настоящее время существуют два подхода к определению мотивации.

1. Первый из них рассматривает мотивацию как структурное образование, как совокупность факторов или мотивов. Его придерживаются многие психологи как отечественные, так и иностранные. «Мотивация – это совокупность факторов, определяющих поведение. Это понятие описывает отношение, существующее между действием и причинами, которые его объясняют или оправдывают». Более определенно высказывается В. И. Ковалев: «Под мотивацией нами понимается совокупность мотивов поведения и деятельности»

2. В рамках второго подхода мотивация рассматривается как динамичное образование, как процесс, поддерживающий психическую активность человека на определенном уровне. Он также имеет своих многочисленных сторонников.

«Мотивация – это процесс психической регуляции, влияющий на направление деятельности и количество энергии, мобилизуемой для выполнения этой деятельности . плана действия.

Е. П. Ильин предлагает схему мотивационного процесса, (когда стимулом является нужда организма) результатом которого оказывается мотив.

1 стадия – это стадия формирования первичного (абстрактного) мотива. Суть ее в формировании потребности личности и побуждения к поисковой деятельности.

2 стадия – это поисковая внешняя или внутренняя активность. В случае, если человек попадаете незнакомую обстановку или не обладает требуемой информацией он вынужден заняться поиском реального объекта во внешней среде.

Внутренняя поисковая активность связана с мысленным перебором конкретных предметов удовлетворения потребности. По сути, это стадия интеллектуальной обработки потребности и воплощения ее в план, цель. Задача этой стадии – в определении субъективной вероятности достижения успеха.

На 3-й стадии осуществляется выбор конкретной цели и формирование намерения ее достижения. На предыдущей стадии цель была определена. При этом она предстает в виде образа будущего результата. Хорошо известно, что самая мучительная для человека процедура – это процедура выбора

Таким образом, на этой стадии возникает намерение достичь цели, выражающееся в сознательном преднамеренном побуждении к действию. Именно это побуждение приводит к действию человека и с его возникновением заканчивается формирование конкретного мотива.

Таким образом, в представлении Е. П. Ильина мотивация предстает как процесс формирования мотива.

47.Структура мотива.

Структура каждого конкретного мотива выступает как основания действия, поступка человека. Е. П. Ильин выделяет в структуре мотива 3 блока:

-потребностный блок, включающий в себя биологические, социальные потребности и долженствование;

-блок внутреннего фильтра, который включает в себя предпочтение по внешним признакам, предпочтение внутреннее (интересы и склонности), декларируемый нравственный контроль (убеждения, идеалы, ценности, установки, убеждения), недекларируемый нравственный контроль (уровень притязаний), оценка своих возможностей (т. е. своих знаний, умений, качеств), оценка своего состояния в данный момент, учет условий своих достижения своих целей, предвидение последствий своих действий, поступков, деятельности в целом;

-целевой блок, куда входят потребностная цель, опредмеченное действие и сам процесс удовлетворения потребности.

В состав мотива могут входить один или несколько компонентов из того или иного блока, один из которых может играть главную роль, а другие – вспомогательную, сопутствующую. Таким образом, в структуре мотива находят отражение несколько причин и целей. Кроме того, такое понимание мотива позволяет по новому взглянуть на так называемое полимотивированное поведение человека. По сути в основании такого поведения лежит не одна, а несколько причин, несколько компонентов, входящих в структуру мотива.

Мотивация – это побуждения, вызывающие активность личности и определяющие её направленность.

Термин мотивация в широком смысле слова используется во всех областях психологии, исследующих причины и механизмы целенаправленного поведения человека и животных.Если рассматривать проблему мотивации в отечественной психологии в плане развития представлений о её сущности и структуре, то можно выделить два основных подхода:

1-ый подход состоит в том, что мотивация рассматривается как система побуждений или мотивов.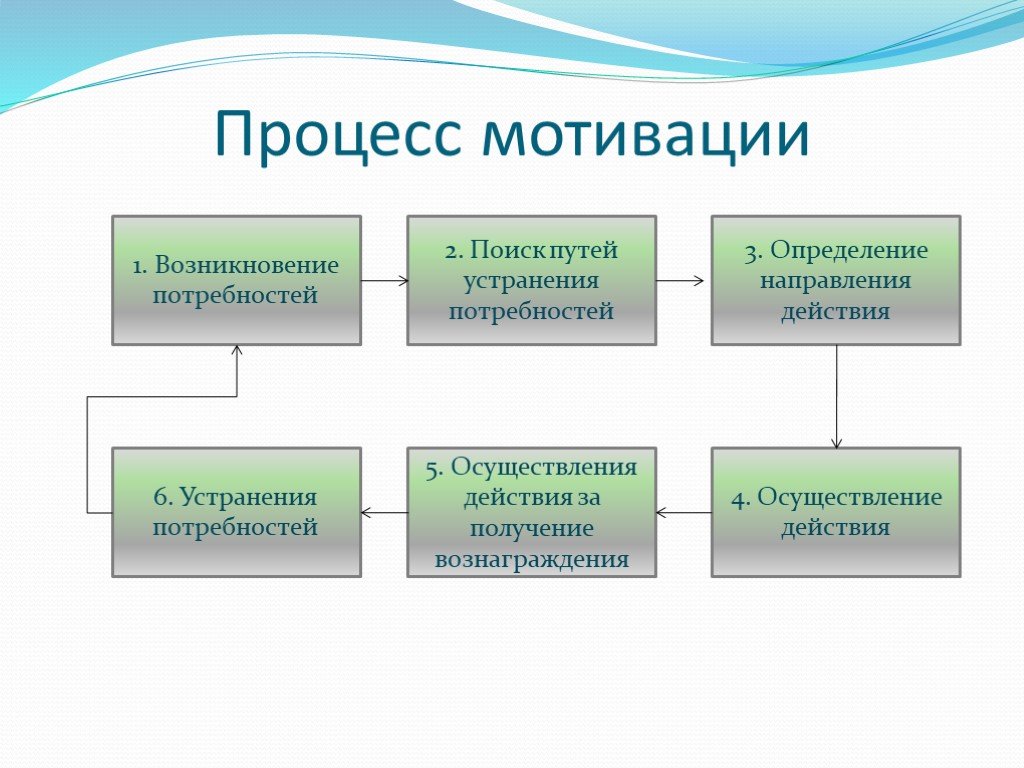 Этот подход реализуется в работах 30-70-х гг. Основные положения этого подхода изложены в работах П.М. Якобсона («Психологические проблемы мотивации поведения человека». 1968 г.).

2-ой подход состоит в том, что мотивация рассматривается как система детерминации поведения человека и животных. Он реализуется в работах Л.Н. Леонтьева («Потребности, мотивы, эмоции»), В.К. Вилюнаса («Психологические механизмы мотивации человека», 1980 г.), В.Г. Асеева («Мотивация поведения и формирования личности», 1976 г.).

Сущность первого подхода состоит в следующем:

В качестве основного в данном подходе выделяется понятие мотива.

Мотив – побуждение, реальный компонент процесса, приводящий к осуществлению человеком целенаправленного действия.Различают мотивы поведения в узком и широком смысле. Мотивация поведения в узком смысле – мотивация конкретных форм поведения человека. _ отдельных поступков, действий). Мотивация в широком смысле слова – совокупность всех психологических моментов, которые определяют поведение человека в целом. Так человек, живущий в обществе, имеющем определённые правила и законы, должен систематически проявлять активность, чтобы существовать и выполнять обязанности члена общества. Эта активность всегда связана у человека с постановкой определённых целей и задач. Таким образом, активность человека целенаправленна. Эта целенаправленность определяет его поведение и поступки. Некоторые цели имеют особо значимый характер. Эти цели порождены желаниями, которые превращаются в побуждения к действию и тем самым приобретают качества мотивов.

Мотивация – это побуждение, определяющее выбор цели.

П.М. Якобсон выделяет следующие виды побуждений (мотивы):

  1. Политические убеждения, нравственные идеалы, представления о будущем, определяющие целенаправленное поведение.

  2. Интересы к получению впечатлений (от искусства, науки, спорта).

  3. Стремление к организации жизни и быта, влечение к труду, семейной жизни, творческой деятельности.

  4. Сильная потребность в чём-либо (знания, деньги, предметы).

  5. Достаточно сильные чувства (признательность, любовь, гнев, ярость, жалость).

  6. Моральные убеждения.

  7. Привычки, нравы, традиции, предрассудки.

  8. Подражание (социальное подражание: мода на одежду, определённые манеры).

Таким образом, первый подход состоит в том, что мотивация рассматривается как система побуждений, мотивов определяющих выбор целей. В этом подходе слабо дифференцирована структура мотивации. Хотя здесь в качестве побуждающих факторов выделяются и потребности, и интересы, и эмоции, и цели.Второй подход, принятый в психологии в последнее время, состоит в том, что мотивация рассматривается как движущая сила человеческого поведения, которая пронизывает все структурные образования личности, её направленность: характер, эмоции, способности и психические процессы. Основным понятием проблемы мотивации является понятие мотивационной сферы личности, изучающей потребности, интересы, мотивы, эмоции, цели.Итак, мотивация или мотивационная сфера личности – это побуждения, вызывающие активность организма и её направленность.

Выделяют 3 группы мотивирующих факторов:

  1. При анализе вопроса о том, почему организм вообще приходит в состояние активности, анализируются проявления потребностей.

  2. Если изучается вопрос: «На что направлена активность организма, ради чего произведён выбор именно этих актов поведения?», исследуется проявление мотивов, как причин, определяющих выбор направленности поведения.

  3. При решении вопроса о том, как осуществляется регуляция динамики поведения, исследуются цели, а также проявления эмоций, субъективных переживаний установок и т.д.

Таким образом, в рамках 2-ого подхода выделяют понятие мотивационной сферы личности, в состав которой входят потребности, мотивы, цели, эмоции.

Необходимо различать мотивацию в поведении человека и животных.

Мотивация— специфический вид регуляции жизнедеятельности, появляющийся лишь на высших ступенях эволюционного развития ( у приматов, млекопитающих).

У животных мотивация как выбор наиболее актуальных потребностей имеет зачаточный характер.

Потребности – основа мотивации, присущей всем живым организмам.

Скрытые мотивы определяют структуру обучения во время адаптивного социального выбора

  • Stewart, A. J. et al. Информационная махинация и недемократические решения. Природа 573 , 117–121 (2019).

    Артикул КАС пабмед Google Scholar

  • Хаузер О.П., Рэнд Д.Г., Пейсахович А. и Новак М.А. Сотрудничество с будущим. Природа 511 , 220–223 (2014).

    Артикул КАС пабмед Google Scholar

  • «>

    Фрейзер, К., Райли, С., Андерсон, Р. М. и Фергюсон, Н. М. Факторы, которые делают вспышку инфекционного заболевания контролируемой. Проц. Натл акад. науч. США 101 , 6146–6151 (2004 г.).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Тененбаум, Дж. Б., Кемп, К., Гриффитс, Т. Л. и Гудман, Н. Д. Как развить разум: статистика, структура и абстракция. Наука 331 , 1279–1285 (2011).

    Артикул КАС пабмед Google Scholar

  • Seuntjens, T.G., Zeelenberg, M., Van De Ven, N. & Breugelmans, S.M. Диспозиционная жадность. Дж. Перс. соц. Психол. 108 , 917–933 (2015).

    Артикул пабмед Google Scholar

  • Фер Э. и Шмидт К. М. Теория справедливости, конкуренции и сотрудничества. QJ Econ. 114 , 817–868 (1999).

    Артикул Google Scholar

  • Болтон Г. и Окенфельс А. ERC: теория справедливости, взаимности и конкуренции. утра. Экон. Ред. 90 , 166–193 (2000).

    Артикул Google Scholar

  • Вебер, Э. У., Блейс, А.-Р. & Betz, NE. Шкала отношения к риску для конкретной области: измерение восприятия риска и поведения, связанного с риском. Дж. Бехав. Реш. Мак. 15 , 263–290 (2002).

    Артикул Google Scholar

  • Канеман Д. и Тверски А. Теория перспектив: анализ решений в условиях риска. Econometrica 47 , 263–292 (1979).

    Артикул Google Scholar

  • Пейсахович А., Новак М. А. и Рэнд Д. Г. Люди демонстрируют «кооперативный фенотип», который является общим и стабильным во времени. Нац. коммун. 5 , 4939 (2014).

    Артикул КАС пабмед Google Scholar

  • Ван Ланге, П. А. М. Стремление к совместным результатам и равенству результатов: интегративная модель ориентации на социальные ценности. Дж. Перс. соц. Психол. 77 , 337–349 (1999).

    Артикул Google Scholar

  • ван Баар Дж. М., Чанг Л. Дж. и Санфей А. Г. Вычислительные и нейронные субстраты моральных стратегий в принятии социальных решений. Нац. коммун. 10 , 1483 (2019).

    Артикул пабмед ПабМед Центральный Google Scholar

  • Poncela-Casasnovas, J. et al. Люди демонстрируют сокращенный набор последовательных поведенческих фенотипов в диадических играх. Науч. Доп. 2 , e1600451 (2016).

    Артикул пабмед ПабМед Центральный Google Scholar

  • ван Баар Дж. М., Клаассен Ф. Х., Риччи Ф., Чанг Л. Дж. и Санфей А. Г. Стабильное распределение мотивов взаимности в популяции. Науч. Респ. 10 , 18164 (2020).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Джара-Эттингер, Дж. Теория разума как обучение с обратным подкреплением. Курс. мнение Поведение науч. 29 , 105–110 (2019).

    Артикул Google Scholar

  • Бриджерс, С., Джара-Эттингер, Дж. и Гвеон, Х. Маленькие дети учитывают ожидаемую полезность обучения других, чтобы решить, чему учить. Нац. Гум. Поведение https://doi.org/10.1038/s41562-019-0748-6 (2019).

  • «>

    Лю, С., Ульман, Т. Д., Тененбаум, Дж. Б. и Спелке, Э. С. Десятимесячные младенцы делают вывод о ценности целей на основе затрат на действия. Наука 358 , 1038–1041 (2017).

    Артикул КАС пабмед Google Scholar

  • Бейкер С.Л., Сакс Р. и Тененбаум Дж.Б. Понимание действия как обратное планирование. Познание 113 , 329–349 (2009).

    Артикул пабмед Google Scholar

  • Бейкер, К.Л., Хара-Эттингер, Дж., Сакс, Р. и Тененбаум, Дж.Б. Рациональная количественная атрибуция убеждений, желаний и восприятий при ментализации человека. Нац. Гум. Поведение 1 , 0064 (2017).

    Артикул Google Scholar

  • Нихонсуги, Т., Ихара, А. и Харуно, М. Избирательное усиление экономических решений, основанных на намерениях, путем неинвазивной стимуляции дорсолатеральной префронтальной коры головного мозга. Дж. Неврологи. 35 , 3412–3419 (2015).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Ведекинд, К. и Милински, М. Сотрудничество посредством оценки изображений у людей. Наука 288 , 850–852 (2000).

    Артикул КАС пабмед Google Scholar

  • Harbaugh, W. T., Mayr, U. & Burghart, D. R. Нейронные реакции на налогообложение и добровольные пожертвования раскрывают мотивы благотворительных пожертвований. Наука 316 , 1622–1625 (2007).

    Артикул КАС пабмед Google Scholar

  • Нив Ю. и др. Обучение с подкреплением в многомерной среде опирается на механизмы внимания. J. Neurosci. 35 , 8145–8157 (2015).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • «>

    Радулеску А., Нив Ю. и Баллард И. Целостное обучение с подкреплением: роль структуры и внимания. Тенденции Познан. науч. 23 , 278–292 (2019).

    Артикул пабмед ПабМед Центральный Google Scholar

  • Леонг Ю. К., Радулеску А., Даниэль Р., Девоскин В. и Нив Ю. Динамическое взаимодействие между обучением с подкреплением и вниманием в многомерных средах. Нейрон 93 , 451–463 (2017).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Коллинз, А. Г. Э. и Франк, М. Дж. Нейронная подпись иерархически структурированных ожиданий предсказывает кластеризацию и передачу наборов правил в обучении с подкреплением. Познание 152 , 160–169 (2016).

    Артикул пабмед ПабМед Центральный Google Scholar

  • «>

    Шапиро, А.С., Роджерс, Т.Т., Кордова, Н.И., Терк-Браун, Н.Б. и Ботвиник, М.М. Нейронные представления событий возникают из временной структуры сообщества. Нац. Неврологи. 16 , 486–492 (2013).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Уилсон, Р. К. и Нив, Ю. Определение актуальности в меняющемся мире. Фронт. Гум. Неврологи. 5 , 189 (2012).

    Артикул пабмед ПабМед Центральный Google Scholar

  • Шапиро, А.С., Терк-Браун, Н.Б., Норман, К.А. и Ботвиник, М.М. Статистическое изучение структуры височного сообщества в гиппокампе. Гиппокамп 26 , 3–8 (2016).

    Артикул пабмед Google Scholar

  • Гершман, С. Дж. и Нив, Ю. Изучение скрытой структуры: вырезание природы в ее суставах. Курс. мнение Нейробиол. 20 , 251–256 (2010).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Кемп С. и Тененбаум Дж. Б. Открытие структурной формы. Проц. Натл акад. науч. США 105 , 10687–10692 (2008 г.).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Хекаторн, Д. Д. Динамика и дилеммы коллективных действий. утра. соц. 61 , 250–277 (1996).

    Артикул Google Scholar

  • Аксельрод, Р. Эффективный выбор в дилемме заключенного. J. Разрешение конфликтов. 24 , 3–25 (1980).

    Артикул Google Scholar

  • Фер, Э. и Фишбахер, У. Социальные нормы и человеческое сотрудничество. Тенденции Cogn. науч. 8 , 185–190 (2004).

    Артикул пабмед Google Scholar

  • Гури, Дж. К., Холт, К. А. и Палфри, Т. Р. Поведение, не склонное к риску, в общих играх с сопоставлением пенни. Игры Экон. Поведение 45 , 97–113 (2003).

    Артикул Google Scholar

  • Бернулли Д. Изложение новой теории измерения риска. Econometrica 22 , 23–36 (1954).

    Артикул Google Scholar

  • Гюйгенс, К. Ценность всех шансов в играх удачи (Вудворд, 1714).

  • Шварц Г. Оценка размерности модели. Энн. Стат. 6 , 461–464 (1978).

    Артикул Google Scholar

  • Хэмптон, А. Н., Боссартс, П. и О’Доэрти, Дж. П. Нейронные корреляты вычислений, связанных с ментализацией, во время стратегических взаимодействий людей. Проц. Натл акад. науч. США 105 , 6741–6746 (2008 г.).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Носензо, Д., Офферман, Т., Сефтон, М. и Ван Дер Вин, А. Дискреционные санкции и вознаграждения в повторной инспекционной игре. Управление. науч. 62 , 502–517 (2016).

    Артикул Google Scholar

  • ФельдманХолл, О. и Шенхав, А. Разрешение неопределенности в социальном мире. Нац. Гум. Поведение 3 , 426–435 (2019).

    Артикул пабмед ПабМед Центральный Google Scholar

  • Гершман, С.Дж., Паунси, Х.Т. и Гвеон, Х. Изучение структуры социального влияния. Познан. науч. 41 , 545–575 (2017).

    Артикул пабмед Google Scholar

  • Шин Ю. С. и Нив Ю. Предвзятые оценки возникают из-за выявления скрытых причин. Нац. Гум. Поведение 5 , 1180–1189 (2021).

    Артикул пабмед ПабМед Центральный Google Scholar

  • Лау, Т., Паунси, Х.Т., Гершман, С.Дж. и Цикара, М. Обнаружение социальных групп с помощью изучения латентной структуры. Дж. Экспл. Психол. Генерал 147 , 1881–1891 (2018).

    Артикул пабмед Google Scholar

  • Джара-Эттингер, Дж. Теория разума как обучение с обратным подкреплением. Курс. мнение Поведение науч. 29 , 105–110 (2019).

    Артикул Google Scholar

  • «>

    Коллетт, С., Паули, В. М., Боссертс, П. и О’Доэрти, Дж. Нейронные вычисления, лежащие в основе обучения с обратным подкреплением в человеческом мозге. eLife 6 , e29718 (2017).

    Артикул пабмед ПабМед Центральный Google Scholar

  • Gobet, F. et al. Механизмы фрагментации в обучении человека. Тенденции Cogn. науч. 5 , 236–243 (2001).

    Артикул КАС пабмед Google Scholar

  • Тальманн М., Соуза А. С. и Оберауер К. Как фрагментация помогает рабочей памяти? Дж. Экспл. Психол. Учиться. Мем. Познан. 45 , 37–55 (2019).

    Артикул пабмед Google Scholar

  • Джонсон, Э. Дж., Камерер, К., Сен, С. и Раймон, Т. Обнаружение ошибок обратной индукции: мониторинг поиска информации в последовательных переговорах. Дж. Экон. Теория 104 , 16–47 (2002).

    Артикул Google Scholar

  • Нагель, Р. Разгадка в играх на угадывание: экспериментальное исследование. утра. Экон. Ред. 85 , 1313–1326 (1995).

    Google Scholar

  • Рапопорт А. Индивидуальные стратегии в игре входа на рынок. Групповое решение. Негот. 4 , 117–133 (1995).

    Артикул Google Scholar

  • Коллок, П. Социальные дилеммы: анатомия сотрудничества. год. Преп. Соц. 24 , 183–214 (1998).

    Артикул Google Scholar

  • Fischbacher, U., Gächter, S. & Fer, E. Являются ли люди условно кооперативными? Доказательства эксперимента общественного блага. Экон. лат. 71 , 397–404 (2001).

    Артикул Google Scholar

  • Курцбан Р. и Хаузер Д. Эксперименты по изучению кооперативных типов у людей: дополнение к эволюционной теории и моделированию. Проц. Натл акад. науч. США 102 , 1803–1807 (2005 г.).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Мур Т. и Зирнсак М. Нейронные механизмы избирательного зрительного внимания. год. Преподобный Психолог. 68 , 47–72 (2017).

    Артикул КАС пабмед Google Scholar

  • Капрариелло, П. А., Кадди, А. Дж. К. и Фиске, С. Т. Социальная структура формирует культурные стереотипы и эмоции: причинно-следственная проверка модели содержания стереотипов. Групповой процесс. Межгрупповое отношение. 12 , 147–155 (2009).

    Артикул Google Scholar

  • Макколи, К., Ститт, К.Л. и Сигал, М. Стереотипы: от предубеждений к предсказаниям. Психология. Бык. 87 , 195–208 (1980).

    Артикул Google Scholar

  • Никерсон, Р. С. Предвзятость подтверждения: повсеместное явление во многих обличьях. Rev. General Psychol. 2 , 175–220 (1998).

    Артикул Google Scholar

  • Пирсон, Э. и др. Крупномасштабный анализ расового неравенства в полиции останавливается в Соединенных Штатах. Нац. Гум. Поведение https://doi.org/10.1016/j.athoracsur.2014.09.078 (2020).

  • Gurekis, T.M. et al. psiTurk: платформа с открытым исходным кодом для проведения воспроизводимых поведенческих экспериментов в Интернете. Поведение. Рез. Методы 48 , 829–842 (2016).

    Артикул пабмед Google Scholar

  • Лихт, А. Н. Игра комиссий по играм: 2 × 2 игры по международному регулированию ценных бумаг. Йель Дж. Междунар. Закон 24 , 61–125 (1999).

    Google Scholar

  • Брамулле, Ю. Антикоординация и социальные взаимодействия. Игры эконом. Поведение 58 , 30–49 (2007).

    Артикул Google Scholar

  • Скирмс, Б. Охота на оленей. Проц. Адреса Ам. Фил. доц. 75 , 31–41 (2001).

    Артикул Google Scholar

  • Фон Нейман, Дж. и Моргенштерн, О. Теория игр и экономическое поведение (Princeton Univ. Press, 1944).

  • «>

    Harris, C.R. et al. Программирование массивов с помощью NumPy. Природа 585 , 357–362 (2020).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • МакКинни, В. Структуры данных для статистических вычислений в Python. В проц. 9-я Python в научной конференции. (под редакцией ван дер Уолт, С. и Миллман, Дж.) 56–61 (2010).

  • Виртанен, П. и др. SciPy 1.0: фундаментальные алгоритмы научных вычислений на Python. Нац. Методы 17 , 261–272 (2020).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Хантер, Дж. Д. Matplotlib: среда 2D-графики. Вычисл. науч. Инженер. 9 , 90–95 (2007).

    Артикул Google Scholar

  • Васком, М.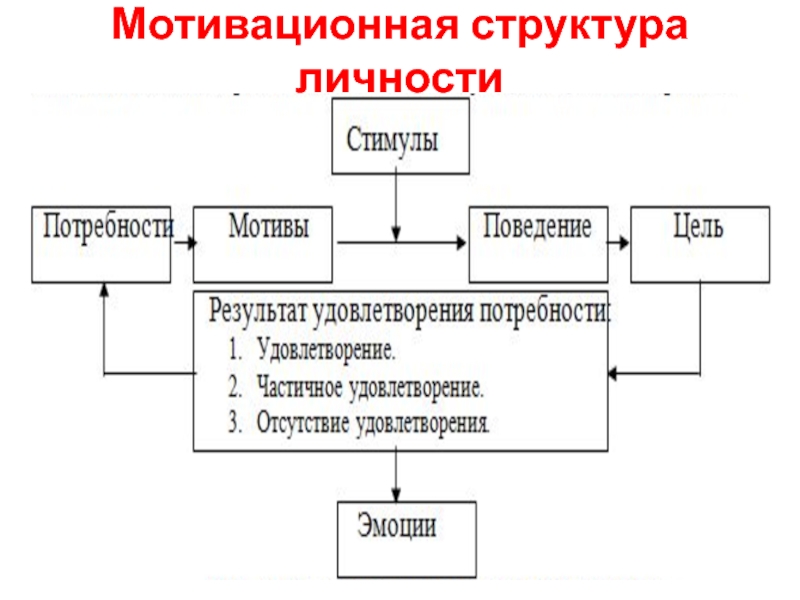 Сиборн: визуализация статистических данных. J. Программное обеспечение с открытым исходным кодом. 6 , 3021 (2021).

    Артикул Google Scholar

  • Мюллер, А. Документация WordCloud для Python, https://amueller.github.io/word_cloud/ (2020).

  • Бейтс Д., Мэхлер М., Болкер Б. и Уокер С. Подгонка линейных моделей смешанных эффектов с использованием lme4. Дж. Стат. ПО 67 , 1–48 (2015).

    Артикул Google Scholar

  • Кузнецова А., Брокхофф П. Б. и Кристенсен Р. Х. Б. Пакет lmerTest: тесты в линейных моделях смешанных эффектов. Дж. Стат. ПО 82 , 1–26 (2017).

    Артикул Google Scholar

    • мотив в nLab

    Пропустить навигационные ссылки | Домашняя страница | Все страницы | Последние версии | Обсудить эту страницу |

    Содержание

    Контекст

    Мотивные когомологии

    Мотив , Мотивные когомологии

    Ингредиенты

    • когомологии

    • стабильная гомотопическая теория

    Определения

    • чистый мотив

      • Чау-мотив

      • числовой мотив

        • периодов, мотивная группа Галуа, космическая группа Галуа

    • смешанный мотив

      • мотив нори

      • Воеводский мотив

        • A1-гомотопическая теория

    • некоммутативный мотив

      • бивариантная алгебраическая K-теория, KK-теория

    • мотивная функция

    • мотивационная интеграция

    • мотивный инвариант Дональдсона-Томаса

    Изменить эту боковую панель

    Когомологии

    когомологии

    • коцикл, кограница, коэффициент

    • гомологии

      • цепь, цикл, граница

    • класс характеристик

      • универсальный класс характеристик

      • вторичный класс характеристик

      • класс дифференциальных характеристик

    • волокнистая последовательность/длинная точная последовательность в когомологиях

    • волоконный ∞-пучок, основной ∞-пучок, связанный ∞-пучок,

      скрученный ∞-пучок

    • ∞-групповое расширение

    • препятствие

    Специальные и общие типы

    • когомологии коцепи

    • обыкновенные когомологии, сингулярные когомологии

    • групповые когомологии, неабелевы групповые когомологии, групповые когомологии Ли

    • Когомологии Галуа

    • группоидные когомологии, неабелевы группоидные когомологии

    • обобщенных (Эйленберга-Стинрода) когомологий

      • кобордизм теория когомологий

      • интегральные когомологии

      • К-теория

      • эллиптических когомологий, tmf

      • таф

    • когомологии абелевых пучков

      • Когомологии Делиня

        • Когомологии де Рама

        • Когомологии Дольбо

      • этальные когомологии

        • группа узлов, группа Пикара, группа Брауэра

      • кристаллические когомологии

      • синтомические когомологии

      • мотивные когомологии

    • когомологии операд

    • Когомологии Хохшильда, циклические когомологии

      • струнная топология

    • неабелевых когомологий

      • основной ∞-пакет

        • универсальное главное ∞-расслоение, групповая модель для универсального главного ∞-расслоения 9структура c, структура String, структура Fivebrane

    • когомологии с постоянными коэффициентами / с локальной системой коэффициентов

    • ∞-когомологии алгебры Ли

      • Когомологии алгебры Ли, когомологии неабелевой алгебры Ли, расширения алгебры Ли, когомологии Гельфанда-Фукса,

    • когомологии биалгебры

    Особые понятия

    • ?ech когомологии 9c структура

  • витые дифференциальные С-структуры

    • витая дифференциальная струнная конструкция, витая дифференциальная пятибранная структура

  • дифференциальные когомологии

    • дифференциальных обобщенных (Эйленберга-Стинрода) когомологий

      • когомологии дифференциальных кобордизмов

      • Когомологии Делиня

      • дифференциальная K-теория

      • дифференциальные эллиптические когомологии

    • дифференциальных когомологий в связном топосе

      • Теория Черна-Вейля

      • ∞-теория Черна-Вейля

  • относительных когомологий

    • Структура Ходжа

    • ориентация в обобщенных когомологиях

    Операции

    • когомологические операции

    • стаканчик продукт

    • связывающий гомоморфизм, гомоморфизм Бокштейна

    • интеграция волокна, нарушение

    • локализация когомологий

    Теоремы

    • теорема об универсальном коэффициенте

    • Теорема Кюннета

    • теорема де Рама, лемма Пуанкаре, теорема Стокса

    • теория Ходжа, теорема Ходжа

      неабелева теория Ходжа, некоммутативная теория Ходжа

    • Теорема Брауна о представимости

    • теорема о гиперпокрытии

    • Двойственность Экманна-Хилтона-Фукса

    Изменить эту боковую панель

    • Идея
    • Конструкции абелевой категории смешанных мотивов
      • Мотивы нори
      • Мотивы Делиня
      • В основе т-структуры по производной категории смешанные мотивы
      • Каталожные номера
    • Конструкции производной категории смешанных мотивов
      • Как гомотопически инвариантные пучки Нисневича с переносами (мотивы Воеводского)
      • Как рациональные устойчивые мотивные гомотопические типы с тривиальным действием элемента Хопфа (мотивы Мореля)
      • Как гомотопически инвариантные этальные пучки без переносов (мотивы Аюба)
      • Как модули над слагаемым рациональной гомотопически инвариантной алгебраической K-теории (мотивы Бейлинсона)
      • Как модули над спектром, представляющим мотивные когомологии над SpecℤSpec \mathbb{Z} (мотивы Шпицвека)
    • Варианты и расширения
    • Связь с другими полями
      • Отношение к физике
      • Отношение к КК-теории
    • Связанные понятия
    • Каталожные номера
      • Общий
      • Связь с теорией Ходжа
      • Связь КК-теории и бивариантной К-теории, К-мотивов
      • По физике

    Идея

    Чтобы выразить это родство этих различных когомологических теорий, я сформулировал понятие «мотив», связанное с алгебраическим многообразием. Этим термином я хочу показать, что это «общий мотив» (или «общая причина»), стоящий за этим множеством когомологических инвариантов, связанных с алгебраическим многообразием, или даже за всеми когомологическими инвариантами, которые априори возможны. (Гротендик, Récoltes et Semailles?)

    Сходство поведения различных когомологий многообразий над полем позволяет предположить, что среди них есть универсальная со значениями в промежуточной абелевой категории, называемой категория мотивов . Идея состоит в том, что каждому многообразию XX соответствует мотив M(X)M(X), так что любая хорошая теория когомологий пропускается через функтор MM. (Здесь не каждый мотив предполагается образом одного многообразия.)

    Теорию чистых мотивов для гладких проективных многообразий отличают от более общей теории смешанных мотивов для произвольных гладких многообразий. До сих пор чистые мотивы и смешанные мотивы определялись лишь условно. Однако существует несколько эквивалентных определений триангулированной тензорной категории, которая обладает всеми предполагаемыми структурными свойствами производной категории смешанных мотивов (за исключением t-структуры, которая делает ее производной категорией).

    Первоначальной реализацией этой идеи Гротендиком является категория мотивов Чжоу, представляющая собой некоторую абелианизацию и пополнение категории промежутков гладких проективных многообразий. Позже была дана более гомотопически-теоретическая версия, мотивы Воеводского или производные мотивы , см. ниже, которые точно охватывают мотивы Чжоу. Более того, существуют определения некоммутативных мотивов , полученные путем перехода к некоммутативной алгебраической геометрии. Наконец, принцип построения мотивов можно адаптировать и к другим разновидностям геометрии. Например, в некоммутативной топологии роль категории некоммутативных мотивов играет КК-теория.

    Конструкции мотивов часто зависят от того, работаем ли мы в простых характеристиках или в нулевой характеристике. Часть формализма включает более общие схемы, чем многообразия.

    Другая важная идея, ведущая к мотивам, состоит в том, что различные теории когомологий приводят к одним и тем же фрагментам информации; следовательно, с этим связана симметрия, имеющая природу теории Галуа. Например, над комплексными числами можно сравнить «реализации» когомологий Бетти и когомологий де Рама. Таким образом, имеется мотивная группа Галуа и, как обычно в случае с представлениями, имеется структура тензорной категории, которая также является жесткой. Таким образом, фактически имеется абелева тензорная категория мотивов. Реконструкция Таннака играет важную роль; для чистых мотивов у нас есть нейтральные категории Таннака, а для смешанных мотивов у нас есть смешанные категории Таннака. Функции на торсоре изоморфизма между «реализациями» соответствуют матрицам периодов в теории Ходжа.

    LL-функции (и, в частности, ζ\дзета-функции) многообразий также являются инвариантами их мотивов. Программа Ленглендса косвенно затрагивает мотивы; в частности, его существенная часть может быть выражена в виде общей гипотезы модулярности, связывающей LL-функции с автоморфными функциями. Большинство глубоких свойств эллиптических кривых имеют мотивную природу, и, в частности, важный шаг доказательства последней теоремы Ферма Уайлсом и Тейлором можно интерпретировать как доказательство частного случая гипотезы модулярности (для эллиптических кривых).

    Конструкции абелевой категории смешанных мотивов

    Общепринятой конструкции ℚ\mathbb{Q}-линейной абелевой категории смешанных мотивов не существует, и ее существование остается предположительным. Однако существуют кандидатные и условные конструкции, полезные на практике.

    Заметим, что «эта» абелева категория смешанных мотивов зависит от выбора базовой схемы СС, и говорят о мотивах (или мотивных пучках ) над СС. Традиционно СС — это спектр поля, часто нулевой характеристики.

    Мотивы Нори

    У Мадхава Нори есть подход к теории мотивов, основанный на своеобразной реконструкции Таннака, так называемой Теореме Таннака Нори . Конструкция Нори безусловно порождает ℚ\mathbb{Q}-таннаковскую категорию смешанных мотивов над любым подполем ℂ\mathbb{C}.

    Мотивы Делиня

    Пьер Делинь дал определение категории смешанных мотивов над числовыми полями как совместимых систем реализаций, по существу связывающих воедино всю структуру, которую должны порождать смешанные мотивы. Этот подход автоматически дает ℚ\mathbb{Q}-таннаковскую категорию смешанных мотивов со всеми желаемыми функторами реализации (Бетти, ℓ\ell-adic, де Рама и кристаллический). Подробнее см. в Делине.

    В качестве основы t-структуры производной категории смешанных мотивов

    Делин впервые предположил, что проще определить производную категорию DM(S,ℚ)DM(S,\mathbb{Q}) мотивов гипотетическая абелева категория смешанных мотивов. Как только это будет сделано, можно в принципе восстановить абелеву категорию как сердцевину t-структуры на DM(S,ℚ)DM(S,\mathbb{Q}). Теперь хорошо понятно, что представляет собой триангулированная категория DM (S, ℚ) DM (S, \ mathbb {Q}) над любой базовой схемой (см. Ниже). Гипотетическая t-структура на DM(S,ℚ)DM(S,\mathbb{Q}), сердцем которой является абелева категория смешанных мотивов над SS, называется Мотивированная Т-образная конструкция .

    Бейлинсон доказал, что над полями нулевой характеристики существование мотивной t-структуры влечет стандартные гипотезы об алгебраических циклах (см.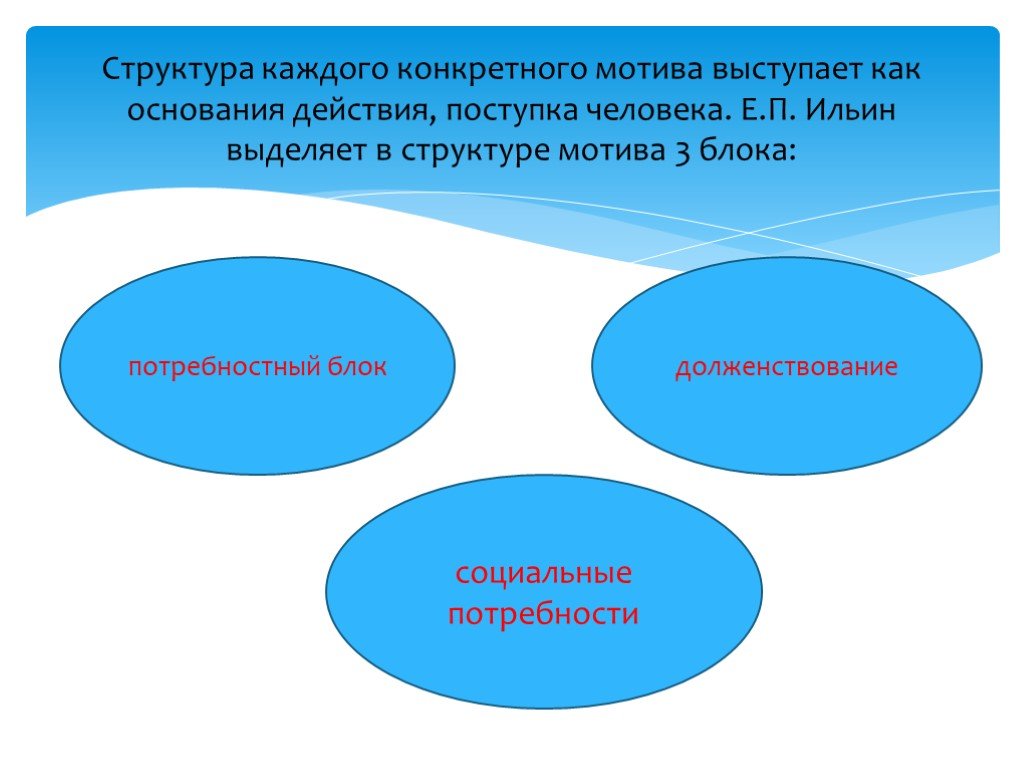 Бейлинсон), а Бондарко доказал, что оно влечет существование мотивной t-структуры для более общих схем ( см. Бондарко).

    Хотя производная категория смешанных мотивов также может быть определена с помощью интегральных, а не рациональных коэффициентов, Воеводский заметил, что производная категория интегральных мотивов не может иметь мотивной t-структуры (Воеводский, предлож. 4.3.8). Таким образом, абелева категория мотивов всегда относится к мотивам с рациональными коэффициентами.

    Литература

    • Александр Бейлинсон, Замечания о стандартных гипотезах Гротендика , 2010, (arXiv)
    • Михаил Бондарко, Смешанные мотивные пучки (и веса для них) существуют, если существуют «обычные» смешанные мотивы , 2013, (arXiv)
    • Pierre Deligne, Le groupe fundamental de la droite Projective moins trois point , (pdf)
    • Владимир Воеводский, Триангулированные категории мотивов над полем , (К-теория)

    Конструкции производной категории смешанных мотивов

    Производная категория гипотетической абелевой категории смешанных мотивов безусловно определена над любой нётеровой схемой. Первое определение было предложено Воеводским в середине 1990-х годов. С тех пор было сформулировано несколько других определений: одно Морелем, одно Аюбом и одно Чисински и Деглизом. Последние три эквивалентны и поддерживают полноценный формализм из шести операций. Однако известно, что они эквивалентны только определению Воеводского выше отличного? и геометрически одноветвистый? схемы.

    С другой стороны, определение Воеводского — единственное из этих четырех, которое также имеет смысл с целыми коэффициентами, а не с рациональными. Недавно, Шпицвек? предложил определение категории интегральных мотивов по общим базовым схемам, которое также поддерживает формализм шести операций. Известно, что оно согласуется с определением Воеводского для полей нулевой характеристики. Однако рационально оно согласуется с определением Мореля/Аюба/Чисински-Деглиза для любой базовой схемы.

    В качестве гомотопически инвариантных пучков Нисневича с переносами (мотивы Воеводского)

    Нётеровой схеме SS соответствует аддитивная категория SmCorSSmCor_S «конечных» соответствий схем,

    • которой

      объекта — гладкие схемы конечного типа над SS;

    • морфизма SmCorS(X,Y)SmCor_S(X,Y) — это абелева группа циклов на расслоенном произведении X×SYX \times_S Y, которые «универсально целы относительно XX» и каждая из компонент которых конечна и сюръективна над ХХ. {eff}_{\geq 0}(S) есть некоторая рефлексивная локализация (∞,1)-категории предпучков с переносами: она состоит из предпучков с трансферами, базовые предпучки которых на Sm/SSm/S являются (∞, 1)-пучками для топологии Нисневича и A1-гомотопически инвариантны. 92=1. Рационально (или даже вдали от 2) получаем пару идемпотентных элементов

      1+ϵ2,1−ϵ2 \frac{1+\epsilon}{2}, \quad \frac{1-\epsilon}{2}

      , которые вызывают расщепление SH(S)ℚ≃SH(S)ℚ+×SH(S)ℚ−SH(S)_{\mathbb{Q}}\simeq SH(S)_{\mathbb{Q} _+}\раз SH(S)_{\mathbb{Q}_-}.

      Определение

      SH(S)ℚ+SH(S)_{\mathbb{Q}_+} является стабильной (∞,1)(\infty,1)-категорией мотивов Мореля .

      Другими словами, мотив Мореля — это рациональный стабильный мотивный гомотопический тип, на котором ε\epsilon действует как −1-1. 91 над СС. Мотивы Мореля также можно охарактеризовать как те рациональные стабильные мотивные гомотопические типы, на которые тривиально действует элемент Хопфа.

      Мы имеем ϵ=−1\epsilon=-1 тогда и только тогда, когда −1-1 является суммой квадратов во всех полях вычетов SS, и в этом случае SH(S)ℚ=SH(S)ℚ+SH (S) _ {\ mathbb {Q}} = SH (S) _ {\ mathbb {Q} _ +}. 1-инвариантных этальных (∞,1)-пучков со значениями в связных рациональных цепных комплексах. 90_{\mathbb{Q}_+} спектра рациональной мотивной сферы, и, следовательно, мотив Бейлинсона — это то же самое, что и мотив Мореля. Они также показали, что мотивы Бейлинсона/Мореля эквивалентны мотивам Аюба. Наконец, они показали, что мотивы Бейлинсона эквивалентны рациональным мотивам Воеводского DM(S,ℚ)DM(S,\mathbb{Q}), когда SS отлично? и геометрически одноветвистый?. Таким образом, в таких схемах все четыре определения производной категории смешанных мотивов эквивалентны.

      Как модули над спектром, представляющим мотивные когомологии над SpecℤSpec \mathbb{Z} (мотивы Шпицвека) 9\ast(M_{\mathbb{Z}}) в SH(S)SH(S). Тогда категории модулей над MSM_S для различных SS наследуют полный формализм шести операций от SHSH.

      Шпицвек определил такую ​​E∞E_\infty-алгебру MℤM_{\mathbb{Z}} такую, что

      • , если SS гладкая над областью Дедекинда, MSM_S представляет мотивные когомологии Блоха-Левина,
      • , если SS гладкая над полем, MSM_S эквивалентна мотивному спектру Эйленберга-Маклейна Воеводского HℤH\mathbb{Z},
      • Mℤ⊗ℚM_{\mathbb{Z}}\otimes\mathbb{Q} — мотив Бейлинсона HBH_B.

      Стабильная (∞,1)(\infty,1)-категория MSM_S-модулей, таким образом, является хорошо себя зарекомендовавшим кандидатом в производную категорию интегральных мотивов, но известно, что она согласуется с определением Воеводского только тогда, когда SS является поле нулевой характеристики (по Рондигсу-Остваеру, теорема 5.5).

      Вариации и расширения

      Соответствия интересны в некоммутативной геометрии аромата операторной алгебры. Например, КК-группы сами по себе являются своего рода соответствиями; У Коннеса и Скандалиса была ранняя ссылка, очень похожая на некоторые идеи из алгебраического мира. Совсем недавно к мотивам в операторно-алгебраической установке подошли Конн, Марколли и другие. 9построена 1-гомотопическая теория и соответствующий аналог категории смешанных мотивов Воеводского; конструкция следует той же базовой схеме.

      Связь с другими областями

      Связь с физикой

      Мотивные структуры проявляются, например, в квантовой теории поля

      • Мотивные кратные значения дзета в амплитудах рассеяния

      • мотивная космическая группа Галуа в перенормировке.

      Квантование «тяни-толкай» в теории Громова-Виттена естественно понимается как «мотивное квантование» в терминах мотивов Чжоу стеков Делиня-Мамфорда (Behrend-Manin 95).

      Связь с КК-теорией

      См. КК-теория в разделе Как аналог мотивов в некоммутативной топологии .

      • чистый мотив, смешанный мотив, мотив Воеводского, мотив нори, мотив чау

      • К-мотив, некоммутативный мотив

      • предварительный пучок с переносом

      • мотивная гомотопическая теория

      • мотивные когомологии

      • дзета-функция, мотивированные множественные дзета-значения

      • Теория Ходжа

      • мотивная функция

      • мотивный инвариант Дональдсона-Томаса

      • Преобразование Фурье-Мукаи

      • См. также КК-теория – Связь с мотивами .

      • мотива в физике

      Каталожные номера

      Общее

      Краткое описание в

      • Барри Мазур, Что такое… Мотив? , Уведомления AMS, том 51, номер 10, 2004 г. (pdf)

      Обзор также находится в главе I книги

      • Ален Конн, Матильда Марколли, Некоммутативная геометрия, квантовые поля и мотивы

      Лекции включают

      • Марк Левин, Шесть лекций по мотивам , лекции на Семинар ICTP по K-теории и мотивам 2006 (pdf)

      Определение мотивов Воеводского можно найти в

      • Карло Мацца, Владимир Воеводский, Чарльз Вейбель, Лекции по мотивным когомологиям (веб-pdf)

      Формализация мотивов Воеводским набросана в

      • Пьер Делин, Лекции Воеводского о кросс-функторах,

        Осень 2001. (pdf)

      и подробно проработан в

      • Джозеф Аюб, Шесть операций Гротендика и формализм исчезающих циклов в мотивирующем мире (I) г., Звездочка, том. 314, соц. Мат. Франция, 2007 г.

        Шесть операций Гротендика и формализм циклов, исчезающих в мотивирующем мире (II) , Asterisque, vol. 315, соц. Мат. Франция, 2007 г.

      определение мотивов Аюба в

      • Джозеф Аюб, Этальная реализация и операции Гротендика (pdf)

      Определение мотивов Бейлинсона и Мореля, эквивалентности различных определений и формализм шести операций см. в

      • Дени-Шарль Чисински, Фредерик Деглиз, Триангулированные категории смешанных мотивов (arXiv)

      Тот факт, что DM(k)DM(k) эквивалентен категории H(ℤ)H(\mathbb{Z})-модулей, если char(k)=0\mathrm{char}(k)=0 доказано в

      • Oliver Röndigs, Paul Arne Østvær, Модули над мотивными когомологиями (pdf)

      Определение Шпицвеком спектра мотивных когомологий над SpecℤSpec \mathbb{Z} находится в

        91-спектр, представляющий мотивные когомологии над областями Дедекинда I (arXiv)

      Краткое изложение аксиом и основных теорем содержится во введении

      • Дени-Шарль Чисински, Фредерик Деглиз, Триангулированные категории смешанных мотивов , arxiv/0912. 2110

      Общий план можно найти во введении к

      • Дмитрий Каледин, Мотивные структуры в некоммутативной геометрии , arxiv/1003.3210

      Некоторые довольно полезные комментарии о мотивах можно найти в этой теме MathOverflow:

      • Что такое «Йога мотивов?»

      См. также сообщение в блоге

      • Дэвид Спейер, Мотивация доказательства гипотезы Вейля (блог)

      Формальное обсуждение мотивов можно найти в лекции 14 из

      • Карло Мацца, Владимир Воеводский и Чарльз Вейбель, Лекции по мотивным когомологиям (веб-pdf)

      Также есть

      • Джеймс С. Милн, Мотивы – Сон Гротендика

      • Минхён Ким, Классические мотивы: Motivic LL-функции

      • Бруно Кан, pdf слайды о чистых мотивах

      • Флоренс Леконт, Натали Вах, Реализация комплексов мотивов Воеводского , архив: 0911. 5611

      • Марк Левин, Гладкие мотивы , arxiv:0807.2265

      • Марк Левин, Смешанные мотивы , Математика. Обзоры и монографии 57 , Амер. Мат. соц. 1998, бесплатный pdf

      Некоммутативный аналог теории мотивов см. в разделе Некоммутативные мотивы.

      Некоторые другие аспекты

      • Бондарко М.В., Весовые конструкции против tt-конструкций; весовые фильтрации, спектральные последовательности и комплексы (по мотивам и вообще) , arxiv/0704.4003

      • Юрий Манин, Мотивы и квантовые когомологии , доклад на Коллоке Гротендика, видео

      Мотивы с точки зрения топосов Гротендика изучаются в

      • Оливия Карамелло, Мотивные топосы, arxiv/1507.06271

      Связь с теорией Ходжа

      Подробное обсуждение связи с теорией Ходжа находится в

      • Крис Питерс, Лекции Тата о мотивных аспектах теории Ходжа (pdf)

      Связь КК-теории и бивариантной К-теории, К-мотивов

      Связь мотивных когомологий с бивариантной алгебраической К-теорией (см. также КК-теория ) обсуждается в

      • Ален Конн, Катерина Консани, Матильда Марколли, Некоммутативная геометрия и мотивы: термодинамика эндомотивов (arXiv:math/0512138)

      • Гильермо Кортиньяс, Андреас Том, Бивариантная алгебраическая K-теория . Дж. Рейн Ангью. Мат. 510 (2007), 71-124. (архив: математика/0603531)

      • Григорий Гаркуша, Иван Панин, K-мотивы алгебраических многообразий (arXiv:1108.0375)

      • Григорий Гаркуша, Алгебраическая Каспаров К-теория. II (архив: 1206.0178)

      См. также КК-теория – Связь с мотивами .

      Собрание литературы см. также в параграфе 1.5 в

      • Эндрю Блумберг, Дэвид Гепнер, Гонсало Табуада, Универсальная характеристика высшей алгебраической К-теории (архив: 1001.2282)

      (в контексте некоммутативных мотивов).

      По физике

      • А. Рей, Матильда Марколли, Мотивы, вводный обзор для физиков (pdf)

      См.

    Добавить комментарий