Разное

Девиация википедия: HTTP 429 — too many requests, слишком много запросов

‎Посмотри внутри by Something Like Z on Apple Music

‎Посмотри внутри by Something Like Z on Apple Music

Уровни

#Гад_же_ты

Стекло

Девиация wiki

Мальвина XXI

Дневники

Твой знак

иZZZнутри

  • Algeria
  • Angola
  • Armenia
  • Azerbaijan
  • Bahrain
  • Benin
  • Botswana
  • Cameroun
  • Cape Verde
  • Chad
  • Côte d’Ivoire
  • Congo, The Democratic Republic Of The
  • Egypt
  • Eswatini
  • Gabon
  • Gambia
  • Ghana
  • Guinea-Bissau
  • India
  • Iraq
  • Israel
  • Jordan
  • Kenya
  • Kuwait
  • Lebanon
  • Liberia
  • Libya
  • Madagascar
  • Malawi
  • Mali
  • Mauritania
  • Mauritius
  • Morocco
  • Mozambique
  • Namibia
  • Niger (English)
  • Nigeria
  • Oman
  • Qatar
  • Congo, Republic of
  • Rwanda
  • Saudi Arabia
  • Senegal
  • Seychelles
  • Sierra Leone
  • South Africa
  • Sri Lanka
  • Tajikistan
  • Tanzania, United Republic Of
  • Tunisia
  • Turkmenistan
  • United Arab Emirates
  • Uganda
  • Yemen
  • Zambia
  • Zimbabwe
  • Australia
  • Bhutan
  • Cambodia
  • 中国大陆
  • Fiji
  • 香港
  • Indonesia (English)
  • 日本
  • Kazakhstan
  • 대한민국
  • Kyrgyzstan
  • Lao People’s Democratic Republic
  • 澳門
  • Malaysia (English)
  • Maldives
  • Micronesia, Federated States of
  • Mongolia
  • Myanmar
  • Nepal
  • New Zealand
  • Papua New Guinea
  • Philippines
  • Singapore
  • Solomon Islands
  • 台灣
  • Thailand
  • Tonga
  • Turkmenistan
  • Uzbekistan
  • Vanuatu
  • Vietnam
  • Armenia
  • Österreich
  • Belarus
  • Belgium
  • Bosnia and Herzegovina
  • Bulgaria
  • Croatia
  • Cyprus
  • Czech Republic
  • Denmark
  • Estonia
  • Finland
  • France (Français)
  • Georgia
  • Deutschland
  • Greece
  • Hungary
  • Iceland
  • Ireland
  • Italia
  • Kosovo
  • Latvia
  • Lithuania
  • Luxembourg (English)
  • Malta
  • Moldova, Republic Of
  • Montenegro
  • Nederland
  • North Macedonia
  • Norway
  • Poland
  • Portugal (Português)
  • Romania
  • Россия
  • Serbia
  • Slovakia
  • Slovenia
  • España
  • Sverige
  • Schweiz
  • Turkey
  • Ukraine
  • United Kingdom
  • Anguilla
  • Antigua and Barbuda
  • Argentina (Español)
  • Bahamas
  • Barbados
  • Belize
  • Bermuda
  • Bolivia (Español)
  • Brasil
  • Virgin Islands, British
  • Cayman Islands
  • Chile (Español)
  • Colombia (Español)
  • Costa Rica (Español)
  • Dominica
  • República Dominicana
  • Ecuador (Español)
  • El Salvador (Español)
  • Grenada
  • Guatemala (Español)
  • Guyana
  • Honduras (Español)
  • Jamaica
  • México
  • Montserrat
  • Nicaragua (Español)
  • Panamá
  • Paraguay (Español)
  • Perú
  • St. Kitts and Nevis
  • Saint Lucia
  • St. Vincent and The Grenadines
  • Suriname
  • Trinidad and Tobago
  • Turks and Caicos
  • Uruguay (English)
  • Venezuela (Español)
  • Canada (English)
  • Canada (Français)
  • United States
  • Estados Unidos (Español México)
  • الولايات المتحدة
  • США
  • 美国 (简体中文)
  • États-Unis (Français France)
  • 미국
  • Estados Unidos (Português Brasil)
  • Hoa Kỳ
  • 美國 (繁體中文台灣)

Девиация и ее формы — Блог Викиум

Девиацией является отклонение в поведении человека, которое нарушает социальные нормы. С точки зрения социологии и обществознания для общества девиация несет в себе угрозу. Все люди понимают данное явление, но при этом на сегодняшний день можно встретить очень много противоправных действий. В этой статье вы узнаете, какие виды и признаки девиации существуют, а также причины появления.

Содержание:

  • 1 Что такое девиация?
  • 2 Типы девиации:
    • 2.1 Признаки девиации
    • 2.2 Причины возникновения девиации


Что такое девиация?

В психологии под определением девиации подразумевается поведение людей, которое способствует нарушению взаимодействия в социуме. Структура девиации включает поведение и моральные ориентации.

Формы и типы девиации

Роберт Мертон выделил основные формы девиации, при этом он рассматривал не совершенный поступок, а пытался выяснить мотив. К негативной форме девиации Мертон отнес все, что человек может делать, чтобы заявить о себе. Согласно его теории, комфортное поведение не относится к девиации, так как оно предполагает подчинение правилам и нормам.

Последователи Мертона поделили формы девиации на негативные и позитивные. В медицине девиацию рассматривают, как любое отклонение в поведении от нормы. Менделевич выделил три формы явления:

  1. Криминальная форма обычно возникает при неудовлетворенности собственной жизнью.
  2. Психопатия подразумевает искаженное восприятие человеком. Чаще всего такие люди признаются невменяемыми.
  3. Аддикция — форма девиации, когда человек пытается уйти от реальности с помощью наркотических средств и алкоголя.

Типы девиации:

  • позитивные отклонения от нормы;
  • негативные девиации, которые проявляются из-за психических болезней;
  • преступные действия;
  • действия, связанные с агрессией;
  • асоциальные действия;
  • негативные действия, не связанные с криминалом.

Можно определить девиации первичного и вторичного типа. При первичной девиации отклонения в поведении никак не наказываются уполномоченными органами. При вторичном типе действия повторяются неоднократно.

Примеры девиации: преступные действия, проституция, жестокость по отношению к животным, излишняя общительность, любовь к азартным играм, вредные привычки.

Признаки девиации

Визуально можно определить девиацию по следующим признакам:

  • агрессивное поведение;
  • болезненное восприятие критики в свой адрес;
  • неумение себя контролировать;
  • наличие психических расстройств;
  • участие в преступных группировках;
  • смена настроения без причины.

Причины возникновения девиации

Психологи выявили и описали причины, которые способствуют развитию девиации:

  • подростковый возраст;
  • низкий интеллект;
  • проблемы с экономикой там, где проживает индивид;
  • финансовые проблемы;
  • воспитание ребенка в неблагоприятной среде;
  • стрессовые ситуации;
  • желание ребенка в подростковом возрасте выглядеть в глазах сверстников лучше;
  • ощущение вседозволенности;
  • стремление прославиться в интернете;
  • особенности восприятия личности;
  • нежелание выполнять что-либо, перекладывая ответственность на других.

Девиация подразумевает поведенческие особенности человека, с помощью которых он хочет обратить на себя внимание общественности. Не всегда такое поведение имеет отрицательный характер, также это может быть и положительная девиация. Если говорить о положительной форме, то такая девиация может принести неоспоримую пользу не только человеку, но и окружающим. Однако все-таки лучше выделяться не поведением, а интеллектуальным развитием. Повысить интеллектуальные способности помогут когнитивные тренажеры Викиум. 

Стандартное отклонение — Простая англоязычная Википедия, бесплатная энциклопедия

График нормального распределения (или колоколообразной кривой). Каждая цветная полоса имеет ширину, равную одному стандартному отклонению.

Набор данных со средним значением 50 (показано синим цветом) и стандартным отклонением (σ) 20.

Пример двух выборочных совокупностей с одинаковым средним значением и разными стандартными отклонениями. Красная популяция имеет среднее значение 100 и SD 10; голубая популяция имеет среднее значение 100 и стандартное отклонение 50.

Стандартное отклонение — это число, используемое для указания того, как измерения для группы отличаются от среднего (среднее или ожидаемое значение). Низкое стандартное отклонение означает, что большинство чисел близки к среднему, а высокое стандартное отклонение означает, что числа более разбросаны. [1] [2]

Сообщаемая погрешность обычно вдвое превышает стандартное отклонение. Ученые обычно сообщают о стандартном отклонении чисел от среднего числа в экспериментах. Они часто решают, что важны только различия, превышающие стандартное отклонение в два или три раза. Стандартное отклонение также полезно в деньгах, где стандартное отклонение заработанных процентов показывает, насколько заработанные проценты одного человека могут отличаться от среднего.

Во многих случаях можно измерить только образец или часть группы. Затем число, близкое к стандартному отклонению для всей группы, можно найти с помощью немного другого уравнения, называемого стандартным отклонением выборки, которое поясняется ниже. В этом случае стандартное отклонение всей группы представлено греческой буквой σ {\ displaystyle \ sigma}, а стандартное отклонение выборки — s {\ displaystyle s}. [3]

Рассмотрим группу, состоящую из следующих восьми чисел:

2, 4, 4, 4, 5, 5, 7, 9 {\ displaystyle 2, \ 4, \ 4, \ 4, \ 5, \ 5, \ 7, \ 9}

Эти восемь чисел имеют среднее (среднее) из 5:

2 + 4 + 4 + 4 + 5 + 5 + 7 + 98 = 5 {\ displaystyle {\ frac {2 + 4 + 4 + 4 + 5 + 5 + 7 + 9} {8}} = 5}

Чтобы рассчитать стандартное отклонение совокупности, сначала найдите отличие каждого числа в списке от среднего. Затем возведите в квадрат результат каждой разницы:

(2−5)2=(−3)2=9(5−5)2=02=0(4−5)2=(−1)2=1(5−5)2=02= 0(4−5)2=(−1)2=1(7−5)2=22=4(4−5)2=(−1)2=1(9{2}=16\\\end{массив}}}

Затем найдите среднее значение этих значений (сумма, деленная на количество чисел). Наконец, извлеките квадратный корень:

(9 + 1 + 1 + 1 + 0 + 0 + 4 + 16) 8 = 2 {\ displaystyle {\ sqrt {\ frac {(9 + 1 + 1 + 1 + 0 + 0 + 4 + 16) {8}}}=2}

Ответом является стандартное отклонение совокупности . Формула верна только в том случае, если восемь чисел, с которых мы начали, представляют собой всю группу. Если они являются лишь частью группы, выбранной случайным образом, то мы можем получить объективную оценку 9.0049 оценивают того, что составляет стандартное отклонение генеральной совокупности, путем деления на 7 (что равно n − 1) вместо 8 (что составляет n ) в нижней части (знаменателе) приведенной выше формулы. Тогда ответом является стандартное отклонение выборки (с поправкой на погрешность) . [4] Это называется поправкой Бесселя. [5] Мы часто используем эту поправку, поскольку выборочная дисперсия, т. е. квадрат выборочного стандартного отклонения, является несмещенной оценкой генеральной дисперсии, другими словами, ожидаемым значением или долгосрочным средним значением выборочной дисперсии. равна генеральной (истинной) дисперсии. Однако это не тот случай, когда стандартное отклонение выборки является объективной оценкой стандартного отклонения генеральной совокупности.[1] Хотя поправка Бесселя является несмещенной оценкой дисперсии, эта оценка имеет более высокую среднеквадратичную ошибку, чем смещенная оценка, или, другими словами, смещенная оценка (то есть деление на n , а не n-1 ) в среднем ближе к истинному значению.

Вот немного более сложный пример из реальной жизни: средний рост взрослых мужчин в Соединенных Штатах составляет 70 дюймов со стандартным отклонением 3 дюйма. Стандартное отклонение в 3 дюйма означает, что большинство мужчин (около 68% при нормальном распределении) имеют рост на 3 дюйма выше и на 3 дюйма ниже среднего (67–73 дюйма) — одно стандартное отклонение. Почти все мужчины (( около 95%) имеют рост на 6 дюймов выше и на 6 дюймов ниже среднего (64–76 дюймов) — два стандартных отклонения. Три стандартных отклонения включают все числа для 99,7% изучаемой выборки населения. Это верно, если распределение нормальное (колоколообразное).

Если бы стандартное отклонение было равно нулю, то все мужчины были бы ростом ровно 70 дюймов. Если бы стандартное отклонение равнялось 20 дюймам, то некоторые мужчины были бы намного выше или намного ниже среднего, с типичным диапазоном роста около 50 дюймов – 90″.

Другой пример: каждая из трех групп {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8} имеет среднее значение 7. Но их стандартные отклонения равны 7, 5 и 1. Третья группа имеет гораздо меньшее стандартное отклонение, чем две другие, потому что все ее числа близки к 7. В общем, стандартное отклонение говорит нам, насколько далеки от среднего остальные числа имеют тенденцию быть, и он будет иметь те же единицы, что и сами числа. Если, например, группа {0, 6, 8, 14} — это возраст группы из четырех братьев в годах, среднее значение равно 7 годам, а стандартное отклонение — 5 годам.

Стандартное отклонение может служить мерой неопределенности. В науке, например, стандартное отклонение группы повторных измерений помогает ученым узнать, насколько они уверены в среднем числе. При принятии решения о том, согласуются ли результаты эксперимента с прогнозом, очень важно стандартное отклонение этих измерений. Если среднее число из экспериментов слишком далеко от предсказанного числа (с расстоянием, измеренным в стандартных отклонениях), то проверяемая теория может быть неверной. Дополнительные сведения см. в разделе интервал прогнозирования.

Примеры применения[изменить | change source]

Понимание стандартного отклонения набора значений позволяет нам узнать, насколько велико ожидаемое отклонение от «среднего» (среднего).

Погода[изменить | change source]

В качестве простого примера рассмотрим средние дневные высокие температуры для двух городов, одного на суше и одного у океана. Полезно понимать, что диапазон дневных высоких температур для городов у океана меньше, чем для городов внутри страны. В этих двух городах может быть одинаковая среднесуточная высокая температура. Однако стандартное отклонение дневной высокой температуры для прибрежного города будет меньше, чем для внутреннего города.

Спорт[изменить | изменить источник]

Другой способ увидеть это — рассмотреть спортивные команды. В любом виде спорта есть команды, которые в чем-то хороши, а в чем-то нет. Команды, занявшие самые высокие места, не будут показывать больших различий в способностях. Они преуспевают в большинстве категорий. Чем ниже стандартное отклонение их способностей в каждой категории, тем более они сбалансированы и последовательны. Однако команды с более высоким стандартным отклонением будут менее предсказуемы. Команда, которая обычно плоха в большинстве категорий, будет иметь низкое стандартное отклонение. Команда, которая обычно хороша в большинстве категорий, также будет иметь низкое стандартное отклонение. Однако команда с высоким стандартным отклонением может быть командой, которая набирает много очков (сильное нападение), но также позволяет другой команде набирать много очков (слабая защита).

Попытка узнать заранее, какие команды выиграют, может включать в себя просмотр стандартных отклонений различных «статистик» команд.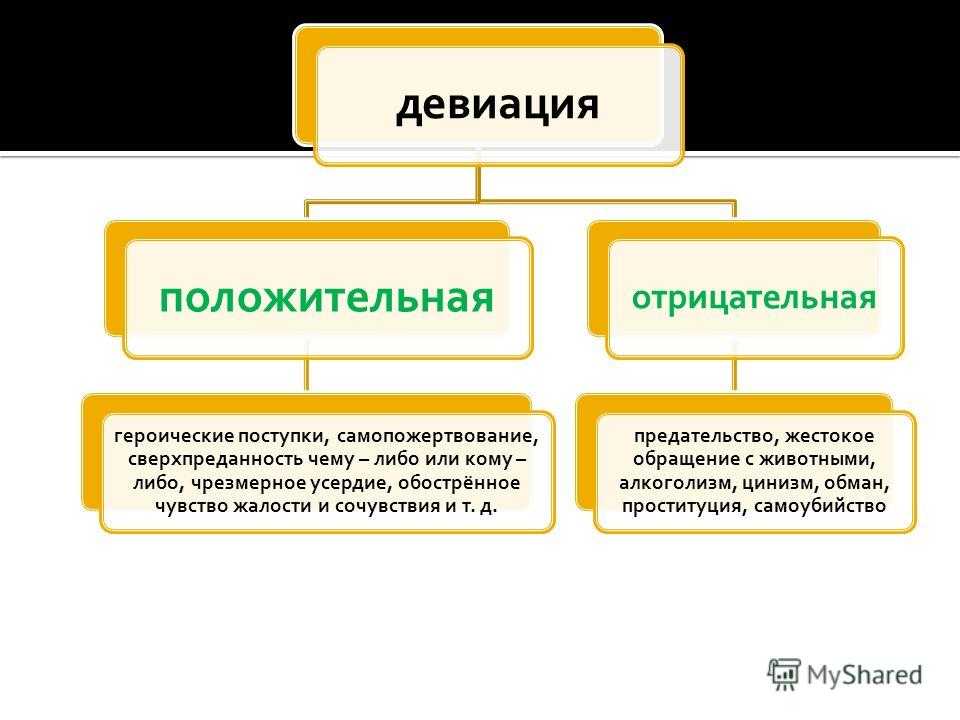 Цифры, которые отличаются от ожидаемых, могут сопоставлять сильные и слабые стороны, чтобы показать, какие причины могут быть наиболее важными для определения того, какая команда победит.

В гонках измеряется время, затрачиваемое водителем на прохождение каждого круга по трассе. Водитель с низким стандартным отклонением времени прохождения круга более постоянен, чем гонщик с более высоким стандартным отклонением. Эта информация может быть использована для понимания того, как водитель может сократить время прохождения круга.

Деньги[изменить | change source]

В деньгах стандартное отклонение может означать риск того, что цена пойдет вверх или вниз (акции, облигации, недвижимость и т. д.). Это также может означать риск того, что группа цен пойдет вверх или вниз [6] (активно управляемые взаимные фонды, индексные взаимные фонды или ETF). Риск — это одна из причин, по которой нужно принимать решения о том, что покупать. Риск — это число, которое люди могут использовать, чтобы узнать, сколько денег они могут заработать или потерять. По мере увеличения риска доход от инвестиций может быть выше ожидаемого («плюс» стандартное отклонение). Однако инвестиции также могут потерять больше денег, чем ожидалось («минус» стандартное отклонение).

Например, человеку нужно было выбрать между двумя акциями. Акция А за последние 20 лет приносила среднюю доходность 10 процентов со стандартным отклонением 20 процентных пунктов (п.п.). Акция Б за последние 20 лет приносила среднюю доходность 12 %, но более высокое стандартное отклонение — 30 п. п. Думая о риске, человек может решить, что Акция А — более безопасный выбор. Даже если они не заработают столько денег, они, вероятно, не потеряют много денег. Человек может подумать, что среднее значение акции B на 2 пункта выше среднего не стоит дополнительных 10 пп стандартного отклонения (больший риск или неопределенность ожидаемой доходности).

Правила для нормально распределенных чисел[изменить | изменить источник]

Темно-синий меньше, чем одно стандартное отклонение от среднего значения. Для нормального распределения это включает 68,27% чисел; в то время как два стандартных отклонения от среднего (средний и темно-синий) включают 95,45 процента; три стандартных отклонения (светлый, средний и темно-синий) включают 99,73 процента; и четыре стандартных отклонения составляют 99,994 процента.

В большинстве математических уравнений для стандартного отклонения предполагается, что числа имеют нормальное распределение. Это означает, что числа распределены определенным образом по обе стороны от среднего значения. 9Нормальное распределение 0009 также называют распределением Гаусса , потому что оно было открыто Карлом Фридрихом Гауссом. [7] Ее часто называют кривой колокола , потому что числа рассредоточены, образуя форму колокола на графике.

Числа не распределяются нормально, если они сгруппированы по одну или по другую сторону от среднего значения. Числа могут быть распределены и при этом оставаться нормально распределенными. Стандартное отклонение говорит о том, насколько широко разбросаны числа.

Связь между средним (средним) и стандартным отклонением[изменить | change source]

Среднее (среднее) и стандартное отклонение набора данных обычно записываются вместе. Тогда человек может понять, что такое среднее число и насколько широко разбросаны другие числа в группе.

То, как распределена группа чисел, также может быть задано коэффициентом вариации (CV), [3] , который представляет собой стандартное отклонение, деленное на среднее значение. Это безразмерное число. Коэффициент вариации часто умножают на 100% и записывают в процентах.

Термин стандартное отклонение впервые был использован в письменной форме Карлом Пирсоном в 1894 году, [8] [9] после того, как он использовал его в лекциях. Это было заменой более ранних названий для той же идеи: например, Гаусс использовал среднюю ошибку . [10]

  • Точность и прецизионность
  • Размер образца
  • Стандартная ошибка
  • Дисперсия
  1. ↑ Гаусс, Карл Фридрих (1816). «Bestimmung der Genauigkeit der Beobachtungen». Zeitschrift für Astronomie und verwandt Wissenschaften . 1 : 187–197.
  2. ↑ Уокер, Хелен (1931). Исследования по истории статистического метода . Балтимор, Мэриленд: Williams & Wilkins Co., стр. 24–25.
  3. ↑ 3.0 3.1 «Список символов вероятности и статистики». Математическое хранилище . 2020-04-26. Проверено 21 августа 2020 г. .
  4. ↑ Вайсштейн, Эрик В. «Стандартное отклонение». mathworld.wolfram.com . Проверено 21 августа 2020 г. .
  5. ↑ «Формулы стандартного отклонения». www.mathsisfun.com . Проверено 21 августа 2020 г. .
  6. ↑ «Что такое стандартное отклонение». Нетронутый. Проверено 29 октября 2011 г. .
  7. ↑ Кирквуд, Бетти Р.; Стерн, Джонатан AC (2003). Основная медицинская статистика . Blackwell Science Ltd. {{цитировать книгу}} : CS1 maint: несколько имен: список авторов (ссылка)
  8. ↑ Додж, Ядола (2003). Оксфордский словарь статистических терминов . Издательство Оксфордского университета. ISBN 0-19-920613-9 .
  9. ↑ Пирсон, Карл (1894). «О вскрытии асимметричных частотных кривых». Фил. Транс. Рой. соц. Лондон, Серия А . 185 : 719–810.
  10. ↑ Миллер, Джефф. «Самые ранние известные случаи использования некоторых слов математики».
  • Простой способ понять стандартное отклонение
  • Стандартное отклонение — объяснение без математики
  • Стандартное отклонение, элементарное введение
  • Стандартное отклонение, более простое объяснение для писателей и журналистов

Отклонения | Megami Tensei Wiki

в: Механика, Persona 5 Royal

Чёрное как смоль отклонение с сильной Тенью.

Отклонения ( Happening»> ハプニング , Хапунингу ) ? — особые области в Мементос в Персона 5 Роял .

Обзор[]

Когда Призрачные воры входят в другую область Мементоса, есть небольшой шанс, что это будет Отклонение. Области, которые являются Отклонениями, будут заметно отличаться от других областей Мементоса. Существует множество различных типов изменений, которые могут произойти при вводе отклонения, и эти изменения могут быть как отрицательными, так и положительными. Одновременно в области отклонения могут действовать до двух типов изменений, однако оба изменения не могут быть полезными для группы; хотя бы одно изменение должно быть отрицательным.

Возможные изменения:

  • Область абсолютно черная, что ограничивает обзор игрока, а мини-карта также недоступна
  • Только сильные тени могут появляться
  • Появится большое количество теней
  • Жнец появляется в начале
  • Есть ловушка
  • Тени бедствий появляются в больших количествах
  • Отброшено большое количество объектов поиска
  • Появится много цветов
  • Появится много сундуков с сокровищами
  • Упрощенная схема карты

При выходе из области отклонений она сбрасывается и становится обычным этажом.

Трофеи и награды[]

Трофей Значок Описание Для Награда
Искаженное познание Обнаружено отклонение в Мементос. P5R трофей

Галерея[]

Линейный путь в Мементос.

Персона 5

символов
Играбельный Главный герой — Моргана — Рюдзи Сакамото — Энн Такамаки — Юсуке Китагава — Макото Нидзима — Футаба Сакура — Хару Окумура — Горо Акэти — Сумире Ёсидзава
Доверенное лицо Игорь — Содзиро Сакура — Чихая Мифунэ — Мунэхиса Иваи — Таэ Такеми — Садайо Каваками — Ичико Охья — Шинья Ода — Хифуми Того — Юки Мисима — Тораносукэ Ёсида — Кэролайн и Жюстин — Саэ Ниидзима — Такуто Маруки
Основные цели Сугуру Камошида — Ичирюсай Мадараме — Джунья Канеширо — Тень Футаба — Куниказу Окумура — Масаеши Шидо — Святой Грааль / Ялдабаоф — Азатот / Адам Кадмон
Прочее Директор Кобаякава — Директор SIU — Шихо Судзуи — Нацухико Наканохара — Мика — Лала Эскарго — Ангел и Джулиан — Меджед — Вакаба Иссики — Сугимура — Президент Танака — Казуя Макигами — Наоя Макигами — Тень Мисима — Шиничи Ёсидзава — Руми — Сибусава — Хосе — Касуми Ёсидзава — тренер Хирагути
Токио Йонген-Джая (кафе Леблан) — Сибуя — Аояма-Итчомэ (Академия Сюдзин) — Синдзюку — Акихабара — Китидзёдзи — Огикубо — Парк Инокашира — Цукисима — Акасака Мицукэ — Суидобаси — Приморский парк Одайба — Ичигая — Икебукуро — Гиндза — Харадзюку — Мэйдзи Храм — Джинбочо — Пляж Миура — Майхама (Токио Дестиниленд) — Канда — Роппонги — Уэно — Асакуса — Чайнатаун ​​- Нагатачо — Синагава — Накано — Старшая школа Косей
Дворец Дворец Камошида — Дворец Мадараме — Дворец Канеширо — Дворец Футабы — Дворец Окумура — Дворец Ниидзимы — Дворец Сидо — Сувениры Шерирут — Глубины воспоминаний — Мир клипот — Путь Да’ат) — Дворец Маруки
Прочее Бархатная комната — Гавайи — Логово воров
Музыка
Альбомы Оригинальный саундтрек ( Persona 5 / Royal (JP / EN))
Песни «Проснись, встань, иди отсюда» — «Жизнь изменится» — «Под маской» — «Последний сюрприз» — «Реки в пустыне» — «Капризы судьбы» — «Токийский дневной свет» — « Хоши То Бокура То» — «Ворваться, чтобы вырваться наружу» — «Бесконечность» — «Темное солнце.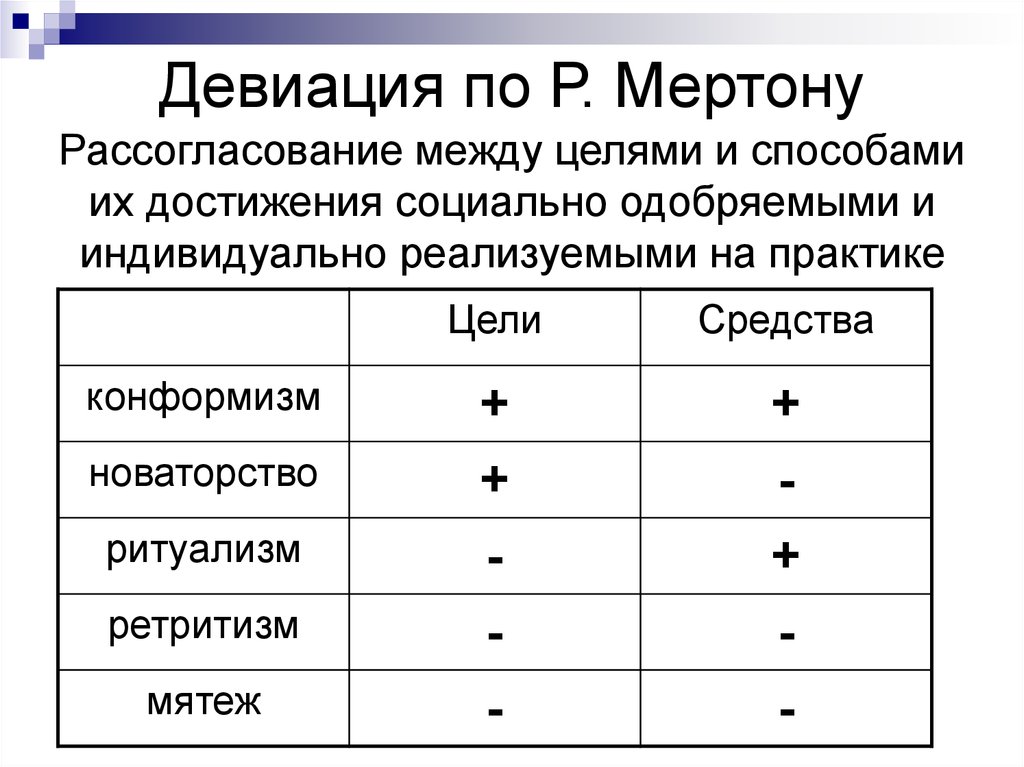 ..» — «Автономия» — «Найти свет» — «СЛИШКОМ ПОЗДНО» — «Цвета летят высоко» — «Возьми Конец» — «Он трикстер☆» — «Я верю» — «Больше нет, что если» — «Выбрось свою маску» — «Бокура но Хикари (Наш свет)»
Архивы
История Персона — Пользователь Персоны — Тень — Я Тени — Второе Пробуждение — Персона Пикаро — Я есть ты — Познание — П. А. Д. — Метавселенная — Навигатор Метавселенной — Маска — Подстановочная карта — Фантомные похитители сердец — Веб-сайт фантомного поклонника — Антисоциальная сила — Сокровище — Полиция — Визитная карточка — Изменение сердца — Психотический срыв — Психическое отключение — Широкая общественность — Семь смертных грехов — Море душ — Бонд — Человек-перо
Школьная жизнь Календарь — Погода — Времена года
Confidant — Социальная статистика — Убежище — Класс — Поезд — Приглашения — Подарки — Украшения
Деятельность Баня — Учеба — Закусочная — Уборка — Кафе для горничных — Бильярд — Книги — DVD — Ретро игры — Кинотеатр — Вызов большого взрыва — Игра с краном — Кровать — Клетки для ватина — Рыболовный пруд — Кроссворды — Дартс — Инструменты проникновения — Кулинария — Обучение — Старый храм — Прачечная — Подработка — Святилище — Исповедь — Джаз Джин — Комнатное растение — Холодильник — ТВ-викторина — Доска — Лавка с напитками — Лотерея — Выращивание — Гадание
Продавцы Магазины: ( Persona 5 / Royal ) — Торговые автоматы — Медицинская клиника Такеми — Неприкасаемые — Магазин Хосе — Программа домашних покупок — Теневые товары Танаки — Военный торговый автомат — Торговля
Призрачная жизнь Запросы на сувениры — Третий глаз — Уровень безопасности — Поиск объектов — Сундуки с сокровищами — Демон сокровищ — Безопасная комната — Гильдия воров — Список теней — Список боссов — Карта навыков — Семена воли — Отклонения
Битва Предметы: ( Персона 5 / Королевский ) — Навыки: ( Персона 5 / Королевский ) — Сложность — Изменения статуса — Слабость Охранники — Тактика — Навигатор Pass — One More — Critical — Technical — Showtime — Cut-in — Тотальная атака — Hold Up — Personality — Drops — Game Over — Disaster Shadow
Follow Up — Harisen Recovery — Endure — Protect — Pocket Pick — Crocodile Tears — Sexy Technique — Down Shot — Bullet Hail — Oda Special — Detox X — Mindfulness
Бархатная комната Список персонажей: ( Персона 5 / Королевский ) — Слияние — Особое слияние — Повешение — Блокировка — Электрический стул — Аркана — Наследование навыков — Несчастный случай слияния — Тревога слияния — Битва вызовов
Система Трофеи: ( Persona 5 / Royal ) — Катсцены — New Game Plus — Патчи и обновления — Элементы профиля Steam
Неиспользованный контент: ( Персона 5 / Королевский )
Развитие
Корпоративный Atlus Co.

Добавить комментарий